Bài tập Công thức Heron tính diện tích tam giác cực hay, chi tiết - Toán lớp 10

Bài tập Công thức Heron tính diện tích tam giác cực hay, chi tiết

Với Bài tập Công thức Heron tính diện tích tam giác cực hay, chi tiết Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Công thức Heron tính diện tích tam giác từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Phương pháp giải

• Công thức Hê – rông dùng để tính diện tích của một tam giác khi biết ba cạnh của tam giác.

• Nội dung công thức Hê – rông:

Cho tam giác ABC có 3 cạnh BC = a, CA = b và AB = c

Gọi p là nửa chu vi tam giác ABC:

 p =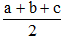

Khi đó ta có diện tích tam giác ABC:

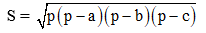
Ngoài ra, công thức Hê – rông còn được viết dưới dạng sau:

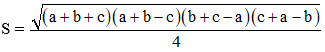
• Phương pháp tìm diện tích tam giác sử dụng công thức Hê – rông:

Bước 1: Tính độ dài các cạnh của tam giác (nếu chưa có)

Bước 2: Tính nửa chu vi tam giác

Bước 3: Tính diện tích tam giác theo công thức Hê – rông.

B. Ví dụ minh họa

Ví dụ 1: Cho tam giác ABC có BC = 9, CA = 6, AB = 5. Tính diện tích tam giác ABC.

Hướng dẫn giải:

Ví dụ 2: Cho tam giác ABC có tạo độ 3 đỉnh A(1;-1), B(3;-3), C(6;0). Tính diện tích tam giác ABC.

Hướng dẫn giải:

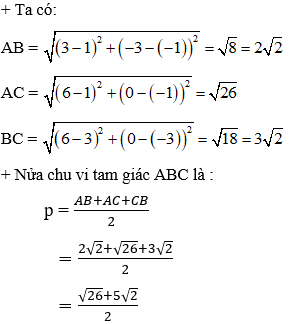
Vậy diện tích tam giác ABC là 6 đvdt.

Ví dụ 3: Cho tam giác ABC có độ dài các đường trung tuyến m_a = 15, m_b = 12, m_c = 9. Tính diện tích tam giác ABC.

Hướng dẫn giải:

Gọi BC = a, AC = b, AB = c

Áp dụng công thức trung tuyến ta có:

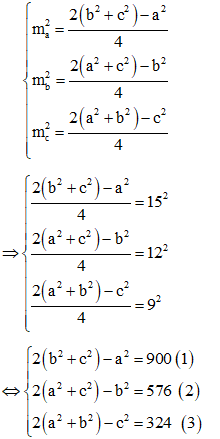
Lấy (1) + (2) + (3), cộng vế theo vế ta được

2(b² + c²) - a² + 2(a² + c²) - b² + 2 (a² + b²) - c² = 900 + 576 + 324

⇔ (2b² - b² + 2b²) + (2c² + 2c² - c²) + (-a² + 2a² + 2a²) = 1800

⇔ 3b² + 3c² + 3a² = 1800

⇔ 3(a² + b² + c²) = 1800

⇔ a² + b² + c² = 600

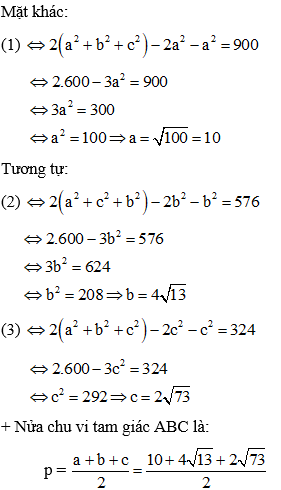
Ví dụ 4: Cho hình chữ nhật ABCD có AB = 4 và BC = 6. Gọi trung điểm của BC là M, N là một điểm trên cạnh CD sao cho ND = 3NC. Diện tích tam giác AMN là:

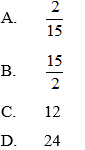
Hướng dẫn giải:

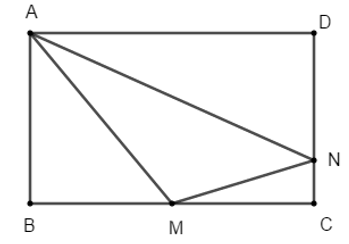
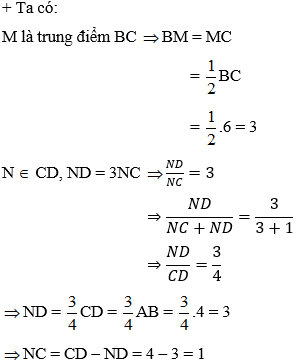
Áp dụng định lý Pyatgo cho các tam giác vuông ABM, MNC và AND ta có:

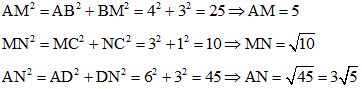
Theo công thức Hê – rông diện tích tam giác AMN là:

+ Ngoài ra, chúng ta có thể tính diện tích tam giác AMN bằng cách sau:

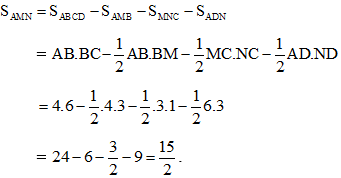
Đáp án B

Ví dụ 5: Cho tam giác ABC có AB = 1, AC = 3. Biết độ dài cạnh BC là một số nguyên. Diện tích của tam giác ABC.

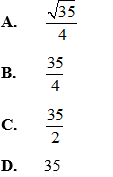
Hướng dẫn giải:

+ Gọi BC = x > 0, x ∈Z

Áp dụng hệ quả định lý Cô – sin trong tam giác ABC, ta có:

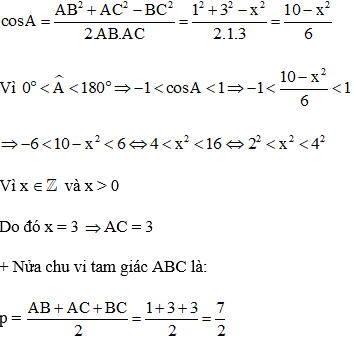
Đáp án A