Cách tính độ dài vecto, khoảng cách giữa hai điểm trong hệ tọa độ cực hay, chi tiết - Toán lớp 10

Cách tính độ dài vecto, khoảng cách giữa hai điểm trong hệ tọa độ cực hay, chi tiết

Với Cách tính độ dài vecto, khoảng cách giữa hai điểm trong hệ tọa độ cực hay, chi tiết Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính độ dài vecto, khoảng cách giữa hai điểm trong hệ tọa độ từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Phương pháp giải

Độ dài vecto

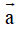
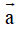
- Định nghĩa: Mỗi vecto đều có một độ dài, đó là khoảng cách giữa điểm đầu và điểm cuối của vecto đó. Độ dài của vecto được ký hiệu là ||.

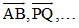
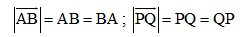
Do đó đối với các vectơ ta có:

- Phương pháp: muốn tính độ dài vectơ, ta tính độ dài cách giữa điểm đầu và điểm cuối của vectơ.

- Trong hệ tọa độ: Cho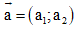

Độ dài vectơ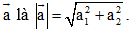

Khoảng cách giữa hai điểm trong hệ tọa độ

Áp dụng công thức sau

Trong mặt phẳng tọa độ, khoảng cách giữa hai điểm M(x_M;y_M) và N(x_N;y_N) là

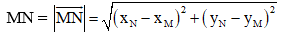
B. Ví dụ minh họa

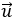
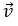
Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho hai vectơ =(4;1) và =(1;4). Tính độ dài vectơ

Hướng dẫn giải:

Ta có:

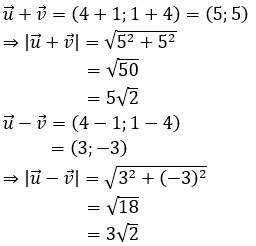
Ví dụ 2: Trong mặt phẳng tọa độ Oxy, tính khoảng cách giữa hai điểm M(1; -2) và N (-3; 4).

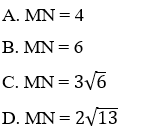
Hướng dẫn giải:

Đáp án D

Ví dụ 3: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 4), B(3; 2), C(5; 4). Chu vi P của tam giác đã cho.

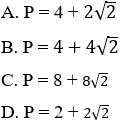
Hướng dẫn giải:

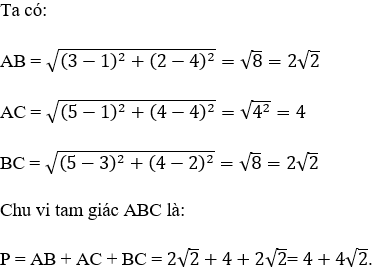
Đáp án B

Ví dụ 4: Trong mặt phẳng tọa độ Oxy, cho bốn điểm A(-1; 1), B(0; 2), C(3; 1) và D(0; -2). Khẳng định nào sau đây là đúng?

A. Tứ giác ABCD là hình bình hành

B. Tứ giác ABCD là hình thoi

C. Tứ giác ABCD là hình thang cân

D. Tứ giác ABCD không nội tiếp được đường tròn

Hướng dẫn giải:

Từ (1) và (2) suy ra ABCD là hình thang cân (hình thang có hai đường chéo bằng nhau là hình thang cân).

Đáp án C

Ví dụ 5: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1;3) và B(4;2). Tìm tọa độ điểm C thuộc trục hoành sao cho C cách đều hai điểm A và B.

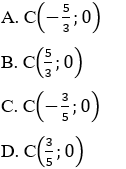
Hướng dẫn giải:

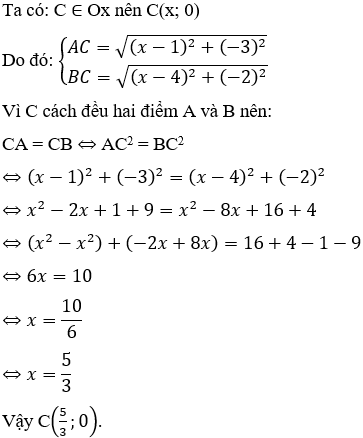
Đáp án B