Cách làm bài tập Giải tam giác lớp 10 cực hay, chi tiết - Toán lớp 10
Cách làm bài tập Giải tam giác lớp 10 cực hay, chi tiết
Với Cách làm bài tập Giải tam giác lớp 10 cực hay, chi tiết Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập làm bài tập Giải tam giác từ đó đạt điểm cao trong bài thi môn Toán lớp 10.
A. Phương pháp giải
Giải tam giác là tìm một số yếu tố của tam giác khi cho biết các yếu tố khác.
Phương pháp: Sử dụng các hệ thức đã được nêu lên trong định lý Cô-sin, định lý sin, công thức trung tuyến và các công thức tính diện tích tam giác, hệ thức lượng trong tam giác vuông,…
Ứng dụng vào thực tế: Ứng dụng vào việc đo đạc (đo khoảng cách, đo chiều cao,…)
Phương pháp: Mô phỏng bài toán thực tế vào bài toán giải tam giác để thực hiện tính toán.
B. Ví dụ minh họa
Ví dụ 1: Cho tam giác ABC có AB = 4, BC = 6, AC =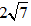 
. Điểm M thuộc đoạn BC sao cho MC = 2MB.
a) Tính cos các góc của tam giác ABC
b) Tính độ dài cạnh AM.
c) Tính diện tích tam giác ABC
d) Tính diện tích tam giác ABM
Hướng dẫn giải:
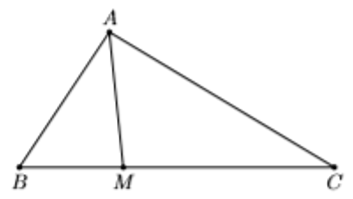
a) Theo hệ quả của định lý Cô – sin trong tam giác ABC ta có:
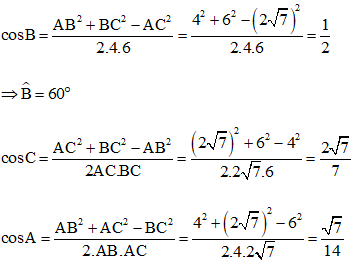
b) Ta có:
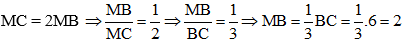
Áp dụng định lý Cô – sin trong tam giác AMB ta có:
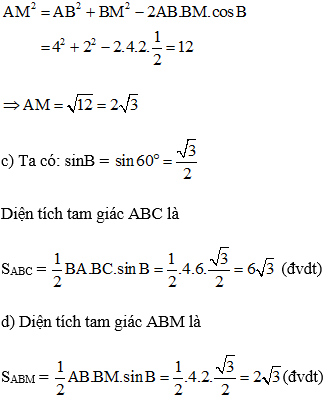
Ví dụ 2: Cho tam giác ABC có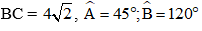 
.
a) Tính các góc và các cạnh còn lại của tam giác ABC.
b) Tính diện tích tam giác ABC.
Hướng dẫn giải:
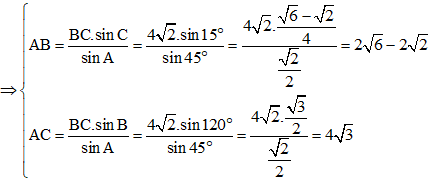
b) Diện tích tam giác ABC là:
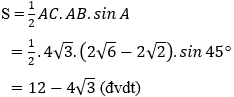
Ví dụ 3: Một cây cột điện cao 20m được đóng trên một triền dốc thẳng nghiêng hợp với phương nằm ngang một góc 17°. Người ta nối một dây cáp từ đỉnh cột điện đến cuối dốc. Tính chiều dài của dây cáp biết rằng đoạn đường từ đáy cọc đến cuối dốc bằng 72m.
Hướng dẫn giải:
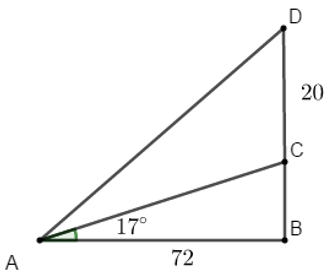
Bài toán được mô phỏng lại như hình vẽ với
A, B, C lần lượt là điểm cuối, chân và đỉnh của triền dốc
C, D lần lượt là chân và đỉnh của cây cột điện
Suy ra chiều dài của dây cáp là đoạn AD
Theo bài ra ta có: CD = 20m; AB = 72m;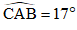 
.
Ta có: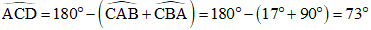 
(góc ngoài tam giác ACB).
Tam giác ABC vuông tại B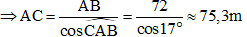 
Áp dụng định lý Cô – sin trong tam giá ACD, ta có:
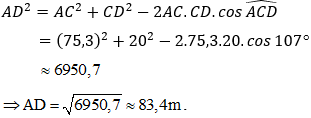
Vậy chiều dài của dây cáp là 83,4m.
Ví dụ 4: Hai chiếc tàu thủy P và Q cách nhau nhau 300m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB trên bờ biển người ta nhìn chiều cao của tháp dưới các góc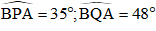 
. Tính chiều cao của hải đăng.
Hướng dẫn giải:
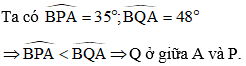
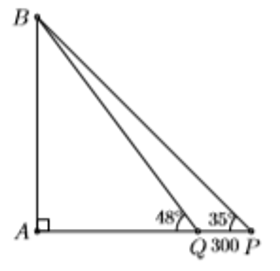
Ví dụ 5: Một cuộc đua thuyền xuất phát từ điểm A như hình vẽ dưới và di chuyển theo hướng tây nam một góc 52° tới điểm B, sau đó di chuyển theo hướng đông nam một góc 40° tới điểm C, cuối cùng quay về điểm A. Điểm C cách điểm A một khoảng 8km. Tính gần đúng tổng khoảng cách của đường đua.
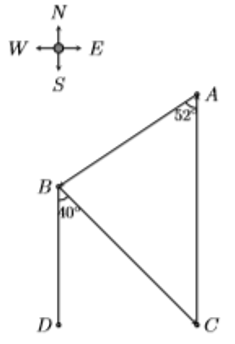
Hướng dẫn giải:
Vậy tổng khoảng cách của đường đua là
S = AB + BC + AC = 5,145 + 6,308 + 8 = 19,453km.
