Cách giải bài tập về Định lí Cô-sin trong tam giác cực hay, chi tiết - Toán lớp 10

Cách giải bài tập về Định lí Cô-sin trong tam giác cực hay, chi tiết

Với Cách giải bài tập về Định lí Cô-sin trong tam giác cực hay, chi tiết Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Định lí Cô-sin trong tam giác từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Phương pháp giải

Áp dụng định lý Cô-sin và hệ quả để giải bài tập

Định lý Cô-sin:

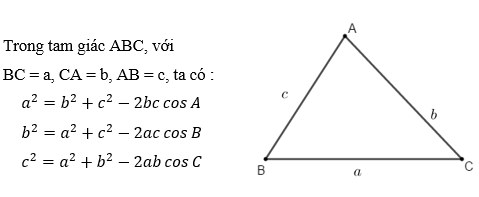
Ý nghĩa của định lý: “Trong một tam giác ta luôn tính được cạnh thứ ba nếu biết trước hai cạnh và góc xen giữa chúng.”

Hệ quả:

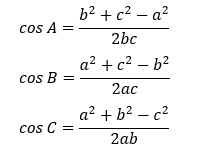
Ý nghĩa của hệ quả: “Trong một tam giác ta luôn tính được các góc nếu biết ba cạnh."

B. Ví dụ minh họa

Ví dụ 1: Cho tam giác ABC có 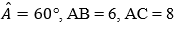. Tính BC.

Hướng dẫn giải:

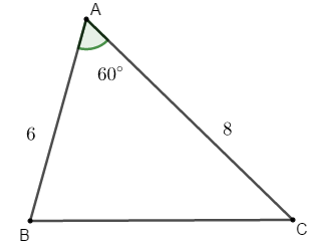
Ví dụ 2: Cho tam giác ABC có cách cạnh 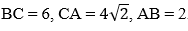. Tính cosA và góc A.

Hướng dẫn giải:

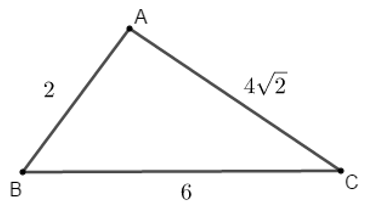
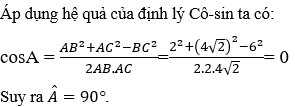
Ví dụ 3: Cho tam giác ABC có AB = 6cm; AC = 5cm và 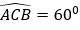. Tính BC?

Hướng dẫn giải:

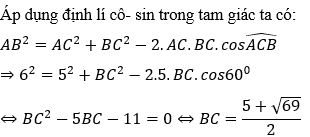
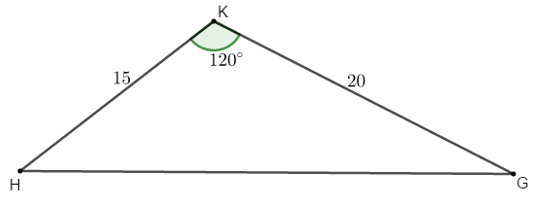
Ví dụ 4: Một ô tô muốn đi từ địa điểm H đến địa điểm G, nhưng giữa H và G là một ngọn núi cao nên ô tô phải đi thành 2 đoạn từ H lên K (ô tô leo dốc lên núi) và từ K đến G (ô tô xuống núi). Các đoạn đường tạo thành tam giác HKG với HK = 15km, KG = 20km và 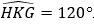. Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.

a, Ô tô đi từ H đến G hết bao nhiêu tiền xăng?

b, Nếu người ta đào một đường hầm xuyên núi chạy thẳng từ H đến G thì ô tô chạy trên con đường mới này tiết kiệm được bao nhiêu kinh phí?

Hướng dẫn giải:

a, Tổng quãng đường mà ô tô phải đi là:

 S = HK + KG = 15 + 20 = 35 km

Ô tô đi hết quãng đường tiêu thụ hết số lít xăng là:

 35 . 0,3 = 10,5 lít

Ô tô đi từ H đến G hết số tiền xăng là:

 10,5 . 13050 = 137025 đồng

b, Ô tô đi thẳng từ H đến G

Áp dụng định lý Cô-sin vào tam giác HKG ta có:

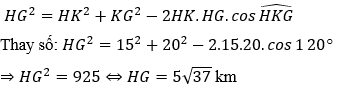
Do đó ô tô phải đi quãng đường là 5√37km và tiêu thụ hết số lít xăng là:

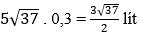
Ví dụ 5: Cho tam giác ABC, có 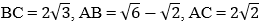. AD là tia phân giác của góc

A. Tính góc BAD

A. 60°

B. 90°

C. 45°

D. 75°

Hướng dẫn giải:

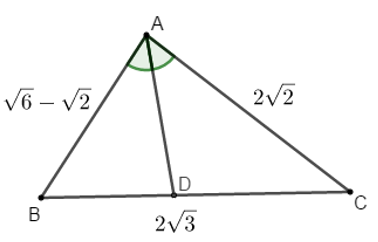
Áp dụng hệ quả định lý Cô-sin trong tam giác ABC, ta có:

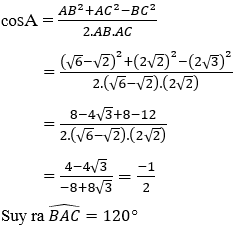
Do AD là phân giác của góc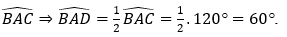

Đáp án A

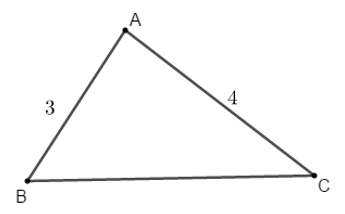
Ví dụ 6: Cho tam giác ABC có AB = 3, AC = 4 và 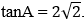Tính BC.

Hướng dẫn giải:

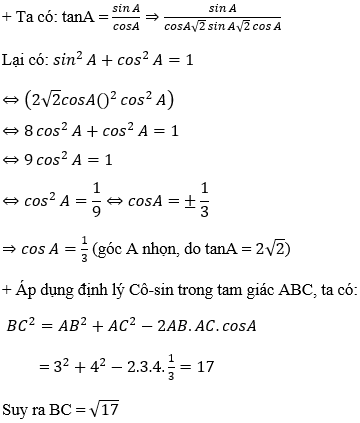
Đáp án D