Công thức, cách tính Diện tích tam giác cực hay, chi tiết - Toán lớp 10

Công thức, cách tính Diện tích tam giác cực hay, chi tiết

Với Công thức, cách tính Diện tích tam giác cực hay, chi tiết Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Công thức, cách tính Diện tích tam giác từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Phương pháp giải

Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức dưới đây.

Cho tam giác ABC có BC = a, CA = b và AB = c, gọi h_a, h_b, h_c là độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB; R và r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp tam giác;

B. Ví dụ minh họa

Ví dụ 1: Cho tam giác ABC có AC = 3, AB = 5, cosA = .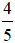

a, Tính diện tích tam giác ABC.

b, Tính đường cao h_a của tam giác ABC.

Hướng dẫn giải:

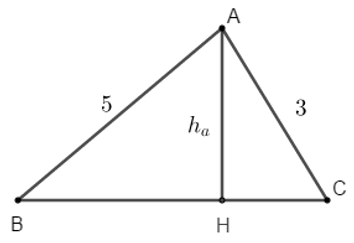
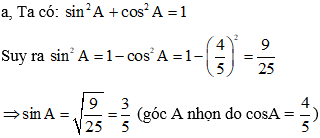
Áp dụng công thức tính diện tích tam giác, ta có diện tích tam giác ABC là:

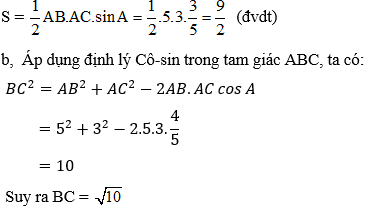
Áp dụng công thức tính diện tích tam giác ABC ta lại có:

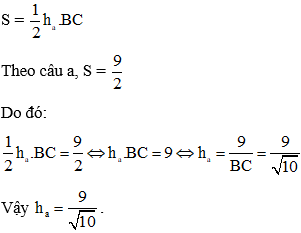
Ví dụ 2: Cho tam giác ABC có 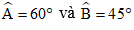và cạnh AC = 4. Tính các cạnh còn lại, diện tích tam giác ABC và đường cao hạ từ đỉnh B.

Hướng dẫn giải:

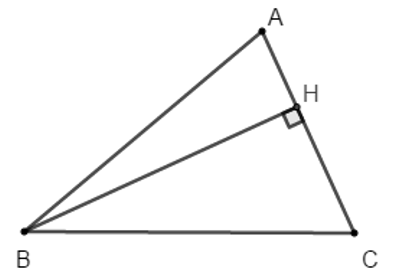
Ví dụ 3: Cho tam giác ABC ngoại tiếp đường tròn tâm O, bán kính r = 5cm. Tính diện tích tam giác ABC biết các cạnh BC = 7cm, CA = 8cm, AB = 10cm.

Hướng dẫn giải:

+ Nửa chu vi tam giác ABC là: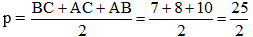

+ Tam giác ABC ngoại tiếp đường tròn tâm O bán kính r = 5cm, nên r là bán kính đường tròn nội tiếp tam giác ABC, áp dụng công thức tính diện tích, ta có diện tích tam giác ABC là:

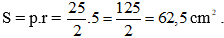
Ví dụ 4: Cho tam giác ABC có các đỉnh A(1; -2), B(-2; 3), C(0; 4). Tính diện tích tam giác ABC.

Hướng dẫn giải:

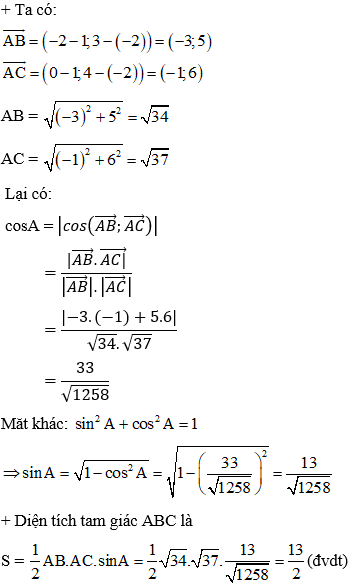
Đáp án A

Ví dụ 5: Cho tam giác ABC vuông tại A có AC = 15 và AB = 8. Diện tích, chu vi và đường cao hạ từ A của tam giác ABC lần lượt là.

Hướng dẫn giải:

+ Tam giác ABC vuông tại A

Do đó diện tích tam giác ABC là: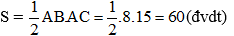

+ Ta có: BC² = AB² + AC² (theo định lý Pytago trong tam giác vuông ABC)

Suy ra: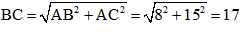

Chu vi tam giác ABC là: C = AB + AC + BC = 8 + 15 + 17 = 40

+ Lại có diện tích tam giác ABC là

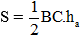
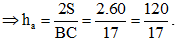
S = (với h_a là độ dài đường cao hạ từ A)

Đáp án B