Cách tìm vecto pháp tuyến của đường thẳng hay, chi tiết - Toán lớp 10

---

Cách tìm vecto pháp tuyến của đường thẳng hay, chi tiết

Với Cách tìm vecto pháp tuyến của đường thẳng hay, chi tiết Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm vecto pháp tuyến của đường thẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Phương pháp giải

Cho đường thẳng d: ax + by + c= 0. Khi đó, một vecto pháp tuyến của đường thẳng d là n→( a;b).

Một điểm M(x₀; y₀) thuộc đường thẳng d nếu: ax₀ + by₀ + c = 0.

B. Ví dụ minh họa

Ví dụ 1: Vectơ pháp tuyến của đường thẳng 2x- 3y+ 7= 0 là :

A. n₄→ = (2; -3)     B. n₂→ = (2; 3)     C. n₃→ = (3; 2)     D. n₁→ = (-3; 2)

Lời giải

Cho đường thẳng d: ax + by + c= 0. Khi đó; đường thẳng d nhận vecto ( a; b) làm VTPT.

⇒ đường thẳng d nhận vecto n→( 2;-3) là VTPT.

Chọn A.

Ví dụ 2. Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng song song với trục Ox?

A. n→( 1; 1)     B. n→( 0; -1)     C. n→(1; 0)     D. n→( -1; 1)

Lời giải

Đường thẳng song song với Ox có phương trình là : y + m= 0 ( với m ≠ 0) .

Đường thẳng này nhận vecto n→( 0; 1) làm VTPT.

Suy ra vecto n'→( 0; -1 ) cũng là VTPT của đường thẳng( hai vecto n→ và n'→ là cùng phương) .

Chọn B.

Ví dụ 3: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng song song với trục Oy?

A. n→( 1; 1)     B. n→( 0; -1)     C. n→(2; 0)     D. n→( -1; 1)

Lời giải

Đường thẳng song song với Oy có phương trình là : x + m= 0 ( với m ≠ 0) .

Đường thẳng này nhận vecto n→(1;0) làm VTPT.

Suy ra vecto n'→( 2; 0 ) cũng là VTPT của đường thẳng( hai vecto n→ và n'→ là cùng phương) .

Chọn D.

Ví dụ 4. Cho đường thẳng ∆: x- 3y- 2= 0. Vectơ nào sau đây không phải là vectơ pháp tuyến của ∆?

A. n₁→ = (1; -3) .    B. n₂→ = (-2; 6) .    C. n₃→ = (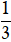 ; -1).    D. n₄→ = (3; 1).

Lời giải

Một đường thẳng có vô số VTPT và các vecto đó cùng phương với nhau.

Nếu vecto n→ ≠ 0→ là một VTPT của đường thẳng ∆ thì k.n→ cũng là VTPT của đường thẳng ∆.

∆ : x - 3y - 2 = 0 → n_d→ = (1; -3) →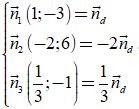

=> Vecto ( 3; 1) không là VTPT của đường thẳng ∆.

Chọn D

Ví dụ 5. Vectơ nào dưới đây là một vectơ pháp tuyến của đường phân giác góc phần tư thứ hai?

A. n→( 1; 1)    B. n→(0; 1)    C. n→(1;0)    D. n→( 1; -1)

Lời giải

Đường phân giác của góc phần tư (II) có phương trình là x + y= 0. Đường thẳng này có VTPT là n→( 1; 1)

Chọn A.

Ví dụ 6. Một đường thẳng có bao nhiêu vectơ pháp tuyến?

A. 1.    B. 2.    C. 4.    D. Vô số.

Lời giải

Một đường thẳng có vô số vecto pháp tuyến. Các vecto đó cùng phương với nhau.

Chọn D.

Ví dụ 7. Vectơ nào dưới đây là một vectơ pháp tuyến của d: 2x- 19y+ 2098= 0?

A. n₁→ = (2;0).    B. n₁→ = (2;2098)    C. n₁→ = (2; -19)    D. n₁→ = (-19;2098)

Lời giải

Đường thẳng ax+ by+ c= 0 có VTPT là n→( a; b) .

Do đó; đường thẳng d có VTPT n→( 2; -19).

Chọn C.

Ví dụ 8: Cho đường thẳng d: x- 2y + 3 = 0. Hỏi đường thẳng d đi qua điểm nào trong các điểm sau?

A. A(3; 0)    B. B(1;2)    C. C(1;2)    D. D(2;-1)

Lời giải

Ta xét các phương án :

+ Thay tọa độ điểm A ta có: 3 - 2.0 + 3 = 0 vô lí

⇒ Điểm A không thuộc đường thẳng d.

+ thay tọa độ điểm B ta có: 1 - 2.2 + 3 = 0

⇒ Điểm B thuộc đường thẳng d.

+ Tương tự ta có điểm C và D không thuộc đường thẳng d.

Chọn B.

Ví dụ 9: Cho đường thẳng d: 2x - 3y + 6 = 0. Điểm nào không thuộc đường thẳng d?

A. A(- 3;0)    B. B(0;2)    C. (3;4)    D. D(1;2)

Lời giải

+ Thay tọa độ điểm A ta được: 2.(-3) - 3.0 + 6 = 0

⇒ Điểm A thuộc đường thẳng d.

+ Thay tọa độ điểm B ta được: 2.0 - 3.2 + 6 = 0

⇒ Điểm B thuộc đường thẳng d.

+ Thay tọa độ điểm C ta có: 2.3 - 3.4 + 6 = 0

⇒ Điểm C thuộc đường thẳng d.

+ Thay tọa độ điểm D ta được : 2.1 - 3.2 + 6 = 2 ≠ 0

⇒ Điểm D không thuộc đường thẳng d.

Chọn D

C. Bài tập vận dụng

Câu 1: Cho đường thẳng d: 2x + 3y - 8 = 0. Trong các vecto sau; vecto nào không là VTPT của đường thẳng d?

A. n₁→( 4; 6)    B. n₂→(-2;-3)    C. n₃→( 4; -6)    D. n₄→(-6;-9)

Lời giải:

Đáp án: C

Trả lời:

+ Đường thẳng d nhận vecto n→( 2; 3) làm VTPT.

+ Lại có; vecto n₁→ = 2n→; n₂→ = - n→ và n₄→ = - 3n→

=> Các vecto n₁→; n₂→; n₄→ cùng phương với vecto n ⃗ nên ba vecto này cũng là VTPT của đường thẳng d.

Câu 2: Cho đường thẳng d: 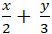= 1. Tìm vecto pháp tuyến của đường thẳng d?

A. n→( 2;3)    B. n→( 3;2)    C. n→( 2; -3)    D. n→( -2;3)

Lời giải:

Đáp án: B

Trả lời:

Đường thẳng d: 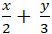= 1 ⇔ (d): 3x + 2y - 6 = 0

⇒ Đường thẳng d nhận vecto n→( 3;2) làm VTPT.

Câu 3: Vectơ nào dưới đây là một vectơ pháp tuyến của d: x - 4y + 2018 = 0

A. n₁→ = (1; 4).    B. n₁→ = (4;1)    C. n₁→ = (2;8)    D. n₁→ = (-2;8)

Lời giải:

Đáp án: D

Trả lời:

Đường thẳng ax + by + c= 0 có VTPT là n→( a; b) .

Do đó; đường thẳng d có VTPT n→(1; - 4).

Lại có; n→(1; -4) và n'→(-2;8) cùng phương nên đường thẳng d nhận vecto n'→(-2;8) làm VTPT.

Câu 4: Cho đường thẳng d: 3x + 5y + 2018 = 0. Tìm mệnh đề sai trong các mệnh đề sau:

A. d có vectơ pháp tuyến n→ = (3; 5)

B. d có vectơ chỉ phương u→ = (5; -3)

C. d có hệ số góc k =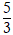

D. d song song với đường thẳng ∆ : 3x + 5y + 9080 = 0.

Lời giải:

Đáp án: C

Trả lời:

Đường thẳng d: 3x+ 5y + 2018= 0 có:

    Vecto pháp tuyến n→(3;5)

    Vecto chỉ phương: u→( 5; 3)

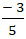
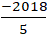
    Từ 3x + 5y + 2018 = 0 suy ra: y = x +

Do đó đường thẳng d có hệ số góc k =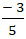

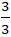
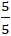
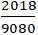
Hai đường thẳng d và ∆ có; = ≠ nên hai đường thẳng này song song với nhau.

Câu 5: Đường thẳng d: 12x - 7y + 5 = 0 không đi qua điểm nào sau đây?

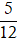
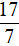
A. M(1; 1)    B. N( -1; -1)    C. P(- ; 0)    D. Q(1; ) .

Lời giải:

Đáp án: B

Trả lời:

Đặt f( x; y) = 12x - 7y + 5. Ta thay tọa độ các điểm vào biểu thức f(x;y) ta được:

+ Thay tọa độ điểm M: f(1; 1) = 12.1 - 7.1 + 5 = 10 ≠ 0

⇒ điểm M không thuộc đường thẳng d.

+ Thay tọa độ điểm N(-1;-1): f(-1; -1) = 12.(-1) – 7.(-1) + 5 = 0

⇒ điểm N thuộc đường thẳng d

+ Tương tự thay tọa độ điểm P và Q vào ta thấy P và Q không thuộc đường thẳng d.

Câu 6: Cho tam giác ABC vuông tại A có A( 1; 2) ; B( 2;4). Tìm một VTPT của đường thẳng AC?

A. n→( 1; -2)    B. n→( 2; 4)    C. n→(-2; 1)    D. n→(2; 1)

Lời giải:

Đáp án: B

Trả lời:

Do tam giác ABC vuông tại A nên AB vuông góc AC.

⇒ Vecto AB→( 1;2) là một VTPT của đường thẳng AC.

Mà AB→( 1;2) cùng phương với vecto n→( 2;4) nên đường thẳng AC nhận vecto

n→( 2; 4)làm VTPT.

Câu 7: Cho tam giác ABC cân tại A. Biết A( 1; -4) và M( -2; 3) là trung điểm của BC. Tìm một VTPT của đường thẳng BC?

A. n→( 1; -4)    B. n→( 3;5)    C. n→(3;-7)    D. n→(5;-3)

Lời giải:

Đáp án: C

Trả lời:

Do tam giác ABC cân tại A lại có AM là đường trung tuyến nên đồng thời là đường cao

⇒ AM vuông góc BC.

⇒ Đường thẳng BC nhận vecto MA→( 3;-7) làm VTPT.

Câu 8: Cho đường thẳng d: 2x - 5y - 10 = 0. Trong các điểm sau; điểm nào không thuộc đường thẳng d?

A. A(5; 0)    B. B(0; -2)    C. C(-5; -4)    D. D(-2; 3)

Lời giải:

Đáp án:

Trả lời:

+ Thay tọa độ điểm A ta được :2.5 - 5.0 - 10 = 0

⇒ Điểm A thuộc đường thẳng d.

+ Thay tọa độ điểm B ta được: 2.0 - 5.(-2) - 10 = 0

⇒ Điểm B thuộc đường thẳng d.

+ Thay tọa độ điểm C ta được : 2.(-5) - 5.(-4) – 10 = 0

⇒ Điểm C thuộc đường thẳng d.

+ Thay tọa độ điểm D vào ta được: 2.(-2) - 5.3 - 10 = - 29 ≠ 0

⇒ Điểm D không thuộc đường thẳng d.