Cách viết phương trình đoạn chắn của đường thẳng hay, chi tiết - Toán lớp 10
Cách viết phương trình đoạn chắn của đường thẳng hay, chi tiết
Với Cách viết phương trình đoạn chắn của đường thẳng hay, chi tiết Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập viết phương trình đoạn chắn của đường thẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 10.
A. Phương pháp giải
+ Cho điểm A(a; 0) và điểm B(0; b) với a.b≠0. Phương trình đường thẳng AB theo đoạn chắn là:
=1
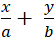
B. Ví dụ minh họa
Ví dụ 1. Phương trình đường thẳng cắt hai trục tọa độ tại A( -2 ;0) và B( 0 ; 5) là:
A. 5x - 2y - 10 = 0 B. 5x - 2y + 10 = 0 C. 2x - 5y - 10 = 0 D. 2x + 5y + 4 = 0
Lời giải
Đường thẳng AB cắt hai trục tọa độ tại A( -2 ; 0) và B( 0 ; 5) nên phương trình đường thẳng AB theo đoạn chắn là :
= 1
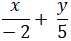
⇔ 5x - 2y + 10 = 0
Chọn B.
Ví dụ 2 : Lập phương trình đường thẳng đi qua điểm M( 5; -3) và cắt hai trục tọa độ tại hai điểm A và B sao cho M là trung điểm của AB.
A. 3x - 5y - 30 = 0 B. 3x + 5y - 30 = 0 C. 5x - 3y - 34 = 0 D. 5x - 3y + 34 = 0
Lời giải
Gọi A ∈ Ox ⇒ A(xA; 0); B ∈ Oy ⇒ B(0; yB)
Ta có M là trung điểm AB ⇒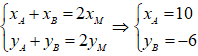 
Suy ra (AB):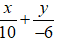 
= 1 ⇔ 3x - 5y - 30 = 0.
Chọn A.
Ví dụ 3 : Có mấy đường thẳng đi qua điểm M( 2; -3) và cắt hai trục tọa độ tại hai điểm A và B sao cho tam giác OAB vuông cân.
A. 2 B. 3 C. 1 D. Không có.
Lời giải
Gọi tọa độ điểm A( a; 0) và B( 0; b).
Phương trình đoạn chắn (AB):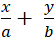
=1
Do tam giác OAB vuông cân tại O ⇔ |a| = |b| ⇔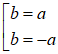 
TH1: b = a ⇒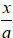 
+ 
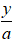
= 1 ⇔ x + y = a
mà M(2; -3) ∈ (AB) ⇒ 2 - 3 = a ⇔ a = -1 ⇒ b = -1
Vậy phương trình (AB) : x + y + 1= 0 .
TH2: b = - a ⇒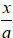
-
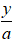
= 1 ⇔ x - y = a
mà M(2; -3) ∈ (AB) ⇒ 2 + 3 = a ⇔ a = 5 ⇒ b = - 5
Vậy phương trình ( AB) : x - y - 5= 0 .
Vậy có hai đường thẳng thỏa mãn đầu bài.
Chọn A.
Ví du 4: Viết phương trình đường thẳng đi qua hai điểm A(0; -3) và B(-2; 0).
A. 2x + 3y - 6 = 0 B. 3x + 2y - 6 = 0 C. 3x + 2y + 6 = 0 D. 2x - 3y - 6 = 0
Lời giải
+ Đường thẳng AB: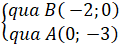 
=> Phương trình đoạn chắn đường thẳng AB: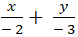 
= 1
Hay (AB) : 3x + 2y + 6 = 0
Chọn C.
Ví dụ 5: Cho đường thẳng d: x - y + 3 = 0. Viết phương trình đường thẳng d dưới dạng đoạn chắn.
A. -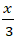 
+ 
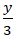
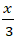
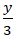
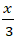
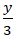
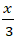
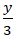
= 1
B.
+
= 1
C. -
-
= 1
D.
-
= 1
Lời giải
Đường thẳng d cắt trục Ox tại A(- 3; 0) và cắt trục Oy tại B(0; 3).
=> Phương trình đoạn chắn đường thẳng d:
-
+
= 1
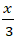
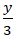
Chọn A.
Ví dụ 6: Cho đường thẳng d: x + y - 6 = 0. Viết phương trình đường thẳng d dưới dạng phương trình đoạn chắn?
A.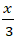
-
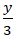
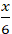
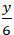
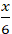
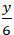
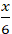
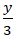
= 1
B. 
- 
= 1
C.
+
= 1
D. -
-
= 1
Lời giải
Đường thẳng d cắt trục Ox tại điểm A(6;0) .
Đường thẳng d cắt trục Oy tại điểm B(0;6).
Đường thẳng d đi qua hai điểm A(6;0) và B(0; 6) nên phương trình đường thẳng d dạng đoạn chắn là:
+
= 1
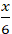
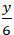
Chọn C.
Ví dụ 7. Phương trình tổng quát của đường thẳng cắt hai trục tọa độ tại A( 3 ; 0) và B(0 ; -2) là:
A. 3x - 2y + 1 = 0 B. -2x + 3y + 6 = 0 C. 2x - 3y + 6 = 0 D. 2x - 3y + 4 = 0
Lời giải
Đường thẳng AB cắt hai trục tọa độ tại A(3 ; 0) và B( 0 ; -2) nên phương trình đường thẳng AB theo đoạn chắn là :
= 1
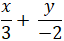
⇔ -2x + 3y + 6 = 0
Chọn B.
Ví dụ 8: Lập phương trình đường thẳng đi qua điểm M( 1;-2) và cắt hai trục tọa độ tại hai điểm A và B sao cho M là trung điểm của AB.
A. – 4x + 2y + 8 = 0 B. 4x + 2y + 8 = 0 C. 2x - y + 1 = 0 D. 2x + y = 0
Lời giải
Gọi A (a ; 0) ∈ Ox; B(0; b) ∈ Oy
Ta có M là trung điểm AB nên :
⇔ a = 2 và b = - 4
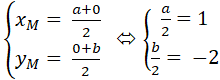
Suy ra phương trình AB :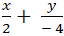 
= 1 hay – 4x + 2y + 8 = 0
Chọn A.
Ví dụ 9 : Có mấy đường thẳng đi qua điểm M(3;3) và cắt hai trục tọa độ tại hai điểm A và B sao cho tam giác OAB vuông cân.
A. 2 B. 3 C. 1 D. Không có.
Lời giải
Gọi tọa độ điểm A( a; 0) và B( 0; b).
Phương trình đoạn chắn đường thẳng AB: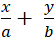
=1
Do tam giác OAB vuông cân tại O ⇔ |a| = |b| ⇔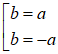
TH1: b = a ⇒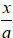
+
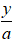
= 1 ⇔ x + y = a
Mà M(3;3) thuộc AB nên 3 + 3 = a ⇔ a= 6 ⇒ b= 6
Vậy phương trình (AB) : x + y - 6 = 0 .
TH2: b = - a ⇒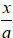
-
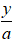
= 1 ⇔ x - y = a
Mà M( 3; 3) thuộc AB nên 3 - 3= a ⇔ a= 0 ⇒ b= 0 ( loại vì khi đó 3 điểm A; B và O trùng nhau)
Vậy có một đường thẳng thỏa mãn đầu bài.
Chọn C.
Ví dụ 10: Viết phương trình đường thẳng đi qua hai điểm A( 0; 4) và B( -3;0).
A. 4x + 3y - 6 = 0 B. 4x - 3y - 6 = 0 C. 4x - 3y + 12 = 0 D. 4x - 3y + 6 = 0
Lời giải
+ Đường thẳng AB: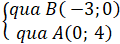 
=> Phương trình đoạn chắn đường thẳng AB: -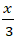
+ 
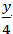
= 1
Hay (AB) : 4x - 3y + 12 = 0
Chọn C.
Ví dụ 11: Cho đường thẳng d: 2x - y + 4 = 0. Viết phương trình đường thẳng d dưới dạng đoạn chắn.
A. -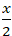 
+
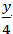
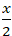
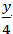
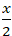
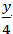
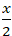
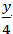
= 1
B.
+ (-
) = 1
C. -
-
= 1
D.
-
= 1
Lời giải
Đường thẳng d cắt trục Ox tại A(-2;0) và cắt trục Oy tại B(0; 4).
=> Phương trình đoạn chắn đường thẳng d:
-
+
= 1
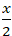
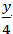
Chọn A
