Cách xác định góc giữa hai đường thẳng cực hay - Toán lớp 10

---

Cách xác định góc giữa hai đường thẳng cực hay

Với Cách xác định góc giữa hai đường thẳng cực hay Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập xác định góc giữa hai đường thẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Phương pháp giải

Để xác định góc giữa hai đường thẳng d và d’ ta có hai cách sau:

+ Cách 1: Gọi n→(x; y) và n'→( x'; y') lần lượt là VTPT của hai đường thẳng d và d’. Gọi α là góc giữa hai đường thẳng. Ta có:

Cosα = |cos⁡( n→; n'→ ) | =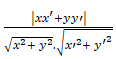

+ Cách 2: Gọi k₁ và k₂ lần lượt là hệ số góc của hai đường thẳng. Gọi α là góc giữa hai đường thẳng. Ta có:

tgα =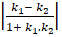

B. Ví dụ minh họa

Ví dụ 1: Tính góc giữa hai đường thẳng (a): 3x + y - 2 = 0 và (b): 2x - y + 39 = 0.

A. 30⁰    B. 60⁰    C. 90⁰    D. 45⁰

Hướng dẫn giải

Đường thẳng: 3x + y - 2 = 0có VTPT n→( 3; 1).

Đường thẳng: 2x - y + 39 = 0 có VTPT n→( 2; -1)

cos(a; b) = |cos⁡( n_a→; n_b→ ) |
=

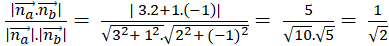
⇒ ( a; b) = 45⁰

Chọn D.

Ví dụ 2: Tìm côsin góc giữa 2 đường thẳng ∆₁ : 10x + 5y - 1 = 0 và ∆₂ :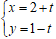

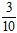
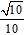
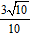
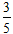
A.    B.    C.    D.

Hướng dẫn:

Vectơ pháp tuyến của ∆₁; ∆₂ lần lượt là n₁→ = (2; 1); n₂→ = (1; 1)

cos(∆₁; ∆₂) = |cos⁡( n₁→, n₂→ ) | =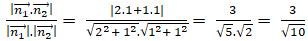

Chọn B.

Ví dụ 3. Tính góc giữa hai đường thẳng: 3x + y - 8 = 0 và 4x – 2y + 10 = 0 .

A. 30⁰    B. 60⁰    C. 90⁰    D. 45⁰

Lời giải

Đường thẳng: 3x + y – 8 = 0 có VTPT n₁→(3; 1)

Đường thẳng: 4x - 2y + 10= 0 có VTPT n₂→(4; -2)

cos(d₁, d₂) = |cos⁡( n₁→, n₂→ ) | = 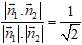⇒ (d₁, d₂) = 45⁰

Chọn D.

Ví dụ 4: Tìm côsin góc giữa 2 đường thẳng d₁: x + 3y - 9 = 0 và d₂:

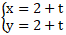
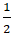
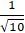
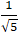
A.    B.    C.    D. tất cả sai

Lời giải

Vectơ pháp tuyến của d₁; d₂ lần lượt là n₁→( 1; 3); n₂→(1; -1).

Cos( d₁; d₂) = |cos⁡( n₁→, n₂→ ) | =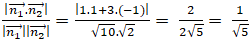

Chọn C.

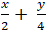
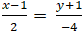
Ví dụ 5 : Tính góc giữa hai đường thẳng: (a): = 1 và (b):

A. 0⁰    B. 45⁰    C. 60⁰    D. 90⁰

Hướng dẫn giải

Đường thẳng (a) ⇔ 4x + 2y - 8 = 0 có VTPT n→( 4; 2)

Đường thẳng (b) có VTCP u→( 2; -4) nên VTPT n'→( 4; 2)

⇒ cos(a; b) = = 1

⇒ Góc giữa hai đường thẳng đã cho là 0⁰.

Chọn A.

Ví dụ 6: Cho đường thẳng (a): x + y - 10 = 0 và đường thẳng (b): 2x + my + 99 = 0. Tìm m để góc giữa hai đường thẳng trên bằng 45⁰.

A. m = -1    B. m = 0    C. m = 1    D. m = 2

Lời giải

Đường thẳng (a) có VTPT n→( 1; 1)

Đường thẳng (b) có VTPT n'→( 2 ;m)

Để góc giữa hai đường thẳng a và b bằng 45⁰ thì

Cos45⁰ =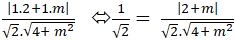

⇔ |2 + m| =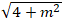

⇔ 4 + 4m + m² = 4 + m²

⇔ 4m = 0 ⇔ m = 0

Chọn B

Ví dụ 7: Cho đường thẳng (a): y = 2x + 3 và (b): y = -x + 6. Tính tan của góc tạo bởi hai đường thẳng (a) và (b)?

A. 1    B. 2    C. 3    D. 4

Lời giải

Gọi α là góc tạo bởi hai đường thẳng (a) và (b).

Đường thẳng (a) có hệ số góc k₁ = 2 và đường thẳng (b) có hệ số góc k₂ = -1.

⇒ Tan của góc tạo bởi hai đường thẳng trên là:

Tgα = 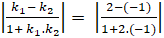= 3

Chọn C.

Ví dụ 8: Cho hai đường thẳng (d₁): y = - 3x + 8 và (d₂) : x + y - 10 = 0. Tính tan của góc tạo bởi hai đường thẳng d₁ và d₂?

A. 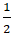   B. 1    C. 3    D.

Lời giải

Đường thẳng (d₁) có hệ số góc k₁ = - 3.

Đường thẳng (d₂) ⇔ y = -x + 10 có hệ số góc k₂ = -1.

⇒ tan của góc tạo bởi hai đường thẳng trên là:

tgα =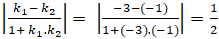

Chọn A.

Ví dụ 9: Cho đường thẳng (a): 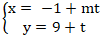và đường thẳng ( b): x + my - 4 = 0. Hỏi có bao nhiêu giá trị của m để góc giữa hai đường thẳng trên bằng 60⁰.

A. 1    B. 2    C. 3    D. 4

Lời giải

+ Đường thẳng (a) có VTCP u→( m, 1) nên có VTPT n→( 1; -m) .

+ Đường thẳng (b) có VTPT n'→( 1; m).

+ Để góc giữa hai đường thẳng trên bằng 60⁰ thì:

Cos60⁰ =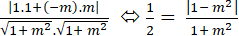

⇔ 1 + m² = 2.|1 - m²| (*)

+ Nếu -1 < m < 1 thì 1 - m² > 0. Từ (*) suy ra: 1 + m² = 2 (1 - m²)

⇔ 1+ m² = 2- 2m² ⇔ 3m² = 1

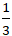
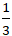
⇔ m² = ⇔ m= ± ( thỏa mãn điều kiện) .

+ Nếu m ≥ 1 hoặc m ≤ -1 thì 1- m² ≤ 0. Từ (*) suy ra:

1 + m² = 2( m² - 1) ⇔ 1 + m² = 2m² - 2

⇔ m² = 3 ⇔ m = ±√3.

Vậy có 4 giá trị của m thỏa mãn.

Chọn D.

C. Bài tập vận dụng

Câu 1: Tìm côsin góc giữa 2 đường thẳng d₁: x + 2y - 7 = 0 và d₂: 2x - 4y + 9 = 0.

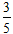
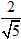
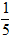
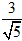
A. -    B.    C.    D.

Lời giải:

Đáp án: A

Trả lời:

Vectơ pháp tuyến của đường thẳng d₁ là n₁→ = (1; 2)

Vectơ pháp tuyến của đường thẳng d₂ là n₂→ = (2; -4)

Gọi φ là góc giữa 2 đường thẳng ta có:

cosφ = = -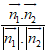

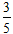
Câu 2: Tìm góc giữa đường thẳng d: 6x - 5y + 15 = 0 và ∆₂:

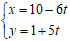
A. 90⁰    B. 30⁰    C. 45⁰    D. 60⁰

Lời giải:

Đáp án: A

Trả lời:

Vectơ pháp tuyến của đường thẳng d là n₁→ = (6; -5)

Vectơ pháp tuyến của đường thẳng ∆₂ là n₂→ = (5; 6)

Ta có n₁→ . n₂→ ⇒ d ⊥ ∆₂.

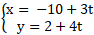
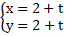
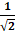
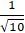
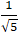
Câu 3: Tìm côsin góc giữa 2 đường thẳng d₁: và d₂:

A.    B.    C.    D. tất cả sai

Lời giải:

Đáp án: D

Trả lời:

Vectơ chỉ phương của d₁; d₂ lần lượt là u₁→(3; 4); u₂→(1; 1).

Cos( d₁; d₂) = |cos⁡(u₁→; u₂→) | =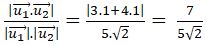

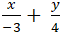
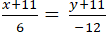
Câu 4: Góc giữa hai đường thẳng: (a): = 1 và (b): gần với số đo nào nhất?

A. 63⁰    B. 25⁰    C. 60⁰    D. 90⁰

Lời giải:

Đáp án: A

Trả lời:

Đường thẳng (a) ⇔ 4x - 3y + 12 = 0 có VTPT n→( 4; -3).

Đường thẳng (b) có VTCP u→( 6; -12) nên VTPT n'→( 2; 1)

⇒ cos(a; b) =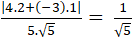

⇒ Góc giữa hai đường thẳng đã cho xấp xỉ 63⁰.

Câu 5: Cho đường thẳng (a): x - y - 210 = 0 và đường thẳng (b): x + my + 47 = 0. Tìm m để góc giữa hai đường thẳng trên bằng 45⁰.

A. m = -1    B. m = 0    C. m = 1    D. m = 2

Lời giải:

Đáp án: B

Trả lời:

Đường thẳng (a) có VTPT n→( 1; -1)

Đường thẳng (b) có VTPT n'→( 1; m)

Để góc giữa hai đường thẳng a và b bằng 45⁰ thì

Cos45⁰ =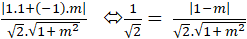

⇔ |1 - m| =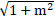

⇔ 1- 2m + m² = 1 + m²

⇔ -2m = 0 ⇔ m = 0

Câu 6: Cho đường thẳng (a): y = -x + 30 và (b): y = 3x + 600. Tính tan của góc tạo bởi hai đường thẳng (a) và (b)?

A. 1    B. 2    C. 3    D. 4

Lời giải:

Đáp án: B

Trả lời:

Gọi α là góc tạo bởi hai đường thẳng (a) và (b).

Đường thẳng (a) có hệ số góc k₁ = -1 và đường thẳng (b) có hệ số góc k₂ = 3.

⇒ Tan của góc tạo bởi hai đường thẳng trên là:

Tgα = 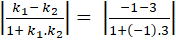= 2

Câu 7: Cho hai đường thẳng (d₁): y = -2x + 80 và (d₂) : x + y - 10 = 0. Tính tan của góc tạo bởi hai đường thẳng d₁ và d₂?

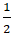
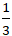
A.    B. 1    C. 3    D.

Lời giải:

Đáp án: D

Trả lời:

Đường thẳng (d₁) có hệ số góc k₁ = - 2.

Đường thẳng (d₂) ⇔ y = -x + 10 có hệ số góc k₂ = -1.

⇒ tan của góc tạo bởi hai đường thẳng trên là:

tgα =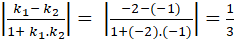

Câu 8: Cho đường thẳng (a): 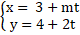và đường thẳng ( b): 2x + y - 40 = 0.Hỏi có bao nhiêu giá trị của m để góc giữa hai đường thẳng trên bằng 45⁰.

A. 1    B. 2    C. 3    D. 4

Lời giải:

Đáp án: B

Trả lời:

+ Đường thẳng (a) có VTCP u→( m; 2) nên có VTPT n→( 2; -m) .

+ Đường thẳng (b) có VTPT n'→( 2;1).

+ Để góc giữa hai đường thẳng trên bằng 45⁰ thì:

Cos45⁰ =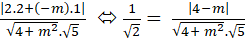

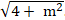
⇔ .√5 = √2|4 - m|

⇔ ( 4 + m²).5 = 2(16 - 8m + m²)

⇔ 20 + 5m² = 32 - 16m + 2m²

⇔ 3m2 + 16m - 12 = 0 ⇔ m = hoặc m = - 6