Cách vẽ Đồ thị hàm số chứa dấu giá trị tuyệt đối hay, chi tiết - Toán lớp 10

Cách vẽ Đồ thị hàm số chứa dấu giá trị tuyệt đối hay, chi tiết

Với Cách vẽ Đồ thị hàm số chứa dấu giá trị tuyệt đối hay, chi tiết Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Đồ thị hàm số chứa dấu giá trị tuyệt đối từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

1. Phương pháp giải.

Vẽ đồ thị (C) của hàm số y = | ax + b | ta làm như sau

Cách 1: Vẽ (C₁ ) là đường thẳng y = ax + b với phần đồ thị sao cho hoành độ x thỏa mãn x ≥ (-b)/a , Vẽ (C₂ ) là đường thẳng y = -ax - b lấy phần đồ thị sao cho x < (-b)/a. Khi đó (C) là hợp của hai đồ thị (C₁ ) và (C₂ ).

Cách 2: Vẽ đường thẳng y = ax + b và y = -ax - b rồi xóa đi phần đường thẳng nằm dưới trục hoành. Phần đường thẳng nằm trên trục hoành chính là (C).

Chú ý:

+ Biết trước đồ thị (C): y = f(x) khi đó đồ thị (C₁ ): y = f(|x|) là gồm phần :

    - Giữ nguyên đồ thị (C) ở bên phải trục tung;

    - Lấy đối xứng đồ thị (C) ở bên phải trục tung qua trục tung.

+ Biết trước đồ thị (C): y = f(x) khi đó đồ thị (C₂ ): y = |f(x)| là gồm phần:

    - Giữ nguyên đồ thị (C) ở phía trên trục hoành

    - Lấy đối xứng đồ thị (C) ở trên dưới trục hoành và lấy đối xứng qua trục hoành.

2. Các ví dụ minh họa.

Ví dụ 1. Vẽ đồ thị của các hàm số sau:

a)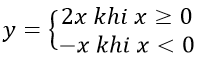

b) y = |-3x + 3|

Hướng dẫn:

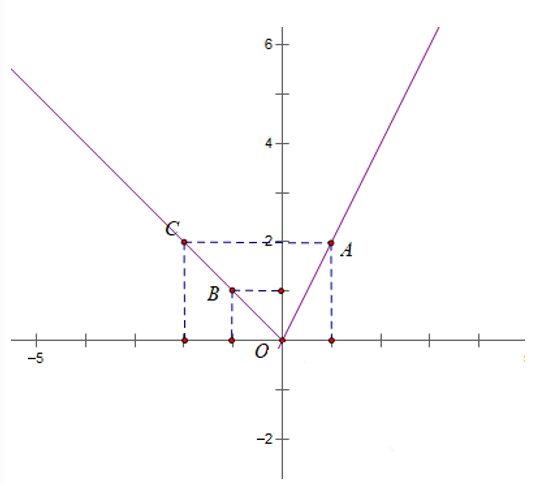
a) Với x ≥ 0 đồ thị hàm số y = 2x là phần đường thẳng đi qua hai điểm A (1; 2) và O(0; 0) nằm bên phải của đường thẳng trục tung.

Với x < 0 đồ thị hàm số y = - x là phần đường thẳng đi qua hai điểm B(-1; 1),

C (-2; 2) nằm bên trái của đường thẳng trục tung.

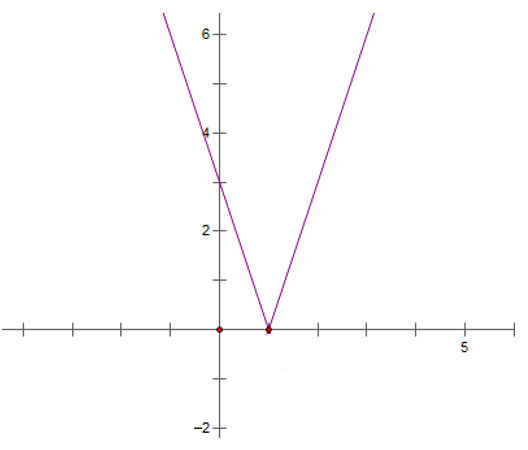
b) Vẽ hai đường thẳng y = -3x + 3 và y = 3x - 3 và lấy phần đường thẳng nằm trên trục hoành.

Ví dụ 2: Vẽ đồ thị của các hàm số sau:

a) y = |x| - 2

b) y = ||x| - 2|

Hướng dẫn:

a) Cách 1: Ta có

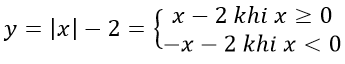
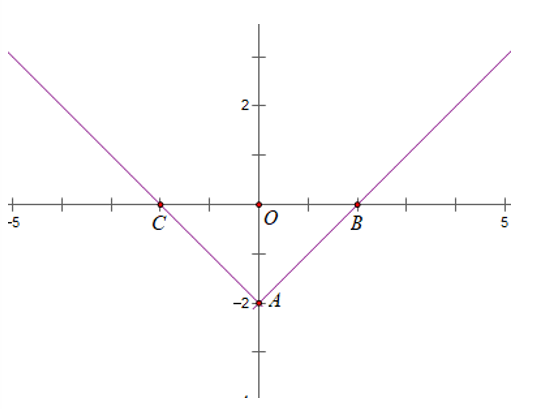
Vẽ đường thẳng y = x – 2 đi qua hai điểm A (0; -2), B (2; 0) và lấy phần đường thẳng bên phải của trục tung

Vẽ đường thẳng y = - x – 2 đi qua hai điểm A (0; -2), B (- 2; 0) và lấy phần đường thẳng bên trái của trục tung.

Cách 2: Đường thẳng d: y = x – 2 đi qua A (0; -2), B (2; 0).

Khi đó đồ thị của hàm số y = |x| - 2 là phần đường thẳng d nằm bên phải của trục tung và phần đối xứng của nó qua trục tung

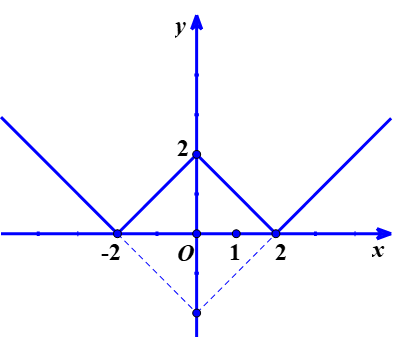
b) Đồ thị y = ||x| - 2| là gồm phần:

- Giữ nguyên đồ thị hàm số y = |x| - 2 ở phía trên trục hoành

- Lấy đối xứng phần đồ thị hàm số y= |x| - 2 ở phía dưới trục hoành.

Ví dụ 3: Lập bảng biến thiên của các hàm số sau:

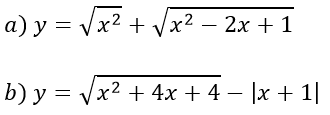
Từ đó tìm giá trị nhỏ nhất và lớn nhất của các hàm số đó trên [-2; 2]

Hướng dẫn:

a) Ta có:

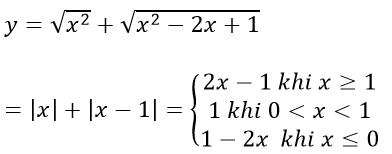
Bảng biến thiên

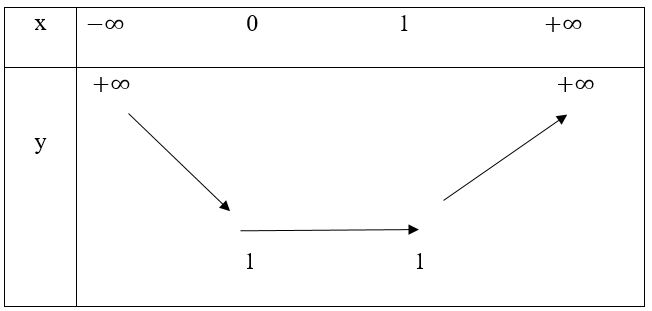
Ta có y(-2) = 5; y(2) = 3

Dựa vào bảng biến thiên ta có:

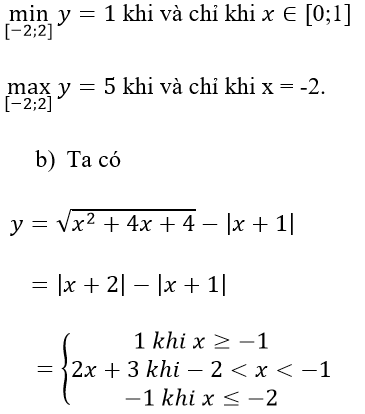
Bảng biến thiên:

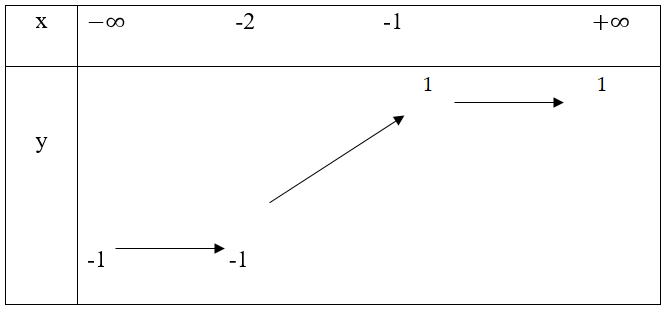
Ta có y(-2) = -1; y(2) = 1

Dựa vào bảng biến thiên ta có: