Ứng dụng của hàm số bậc nhất chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất - Toán lớp 10
Ứng dụng của hàm số bậc nhất chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất
Với Ứng dụng của hàm số bậc nhất chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Ứng dụng của hàm số bậc nhất chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất từ đó đạt điểm cao trong bài thi môn Toán lớp 10.
1. Phương pháp giải.
Cho hàm số f(x) = ax + b và đoạn [α; β] ⊂ R.Khi đó, đồ thị của hàm số y = f(x) trên [α; β] là một đoạn thẳng nên ta có một số tính chất:
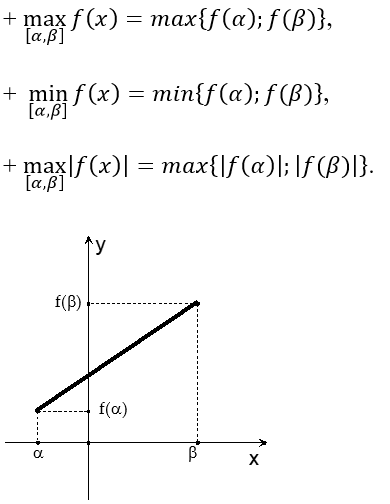
Áp dụng các tính chất đơn giản này cho chúng ta cách giải nhiều bài toán một cách thú vị, ngắn gọn, hiệu quả.
2. Các ví dụ minh họa.
Ví dụ 1: Cho hàm số f(x) = |2x - m|. Tìm m để giá trị lớn nhất của f(x) trên [1; 2] đạt giá trị nhỏ nhất.
Hướng dẫn:
Dựa vào các nhận xét trên ta thấy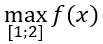
chỉ có thể đạt được tại x = 1 hoặc x = 2.
Như vậy nếu đặt
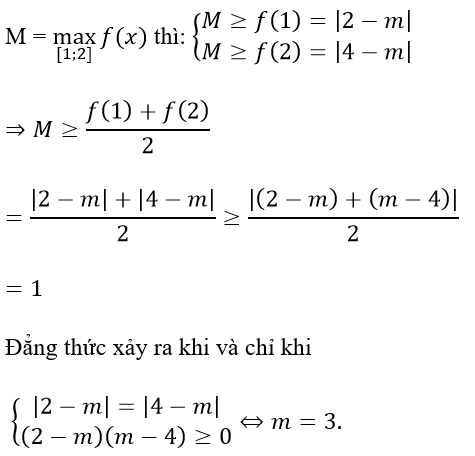
Vậy giá trị nhỏ nhất của M là 1, đạt được chỉ khi m = 3.
Ví dụ 2: Cho hàm số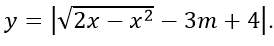
Tìm m để giá trị lớn nhất của hàm số y là nhỏ nhất.
Hướng dẫn:
Gọi A = maxy. Ta đặt
Vậy giá trị cần tìm là m = 3/2.
