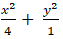Lập phương trình Elip đi qua 2 điểm hoặc qua 1 điểm thỏa mãn điều kiện - Toán lớp 10

---

Lập phương trình Elip đi qua 2 điểm hoặc qua 1 điểm thỏa mãn điều kiện

Với Lập phương trình Elip đi qua 2 điểm hoặc qua 1 điểm thỏa mãn điều kiện Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Lập phương trình Elip đi qua 2 điểm hoặc qua 1 điểm thỏa mãn điều kiện từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Phương pháp giải

+ Bài toán 1: Lập phương trình elip (E) đi qua hai điểm A và B :

- Bước 1: Gọi phương trình chính tắc của elip( E) : 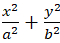= 1 (a > b > 0).

- Bước 2: Do hai điểm A và B thuộc elip (E) nên thạy tọa độ hai điểm này vào phương trình ( E) ta được hai phương trình ẩn a²; b².

Giải hệ phương trình ta được a²; b²...

⇒ Phương trình chính tắc của elip.

+ Bài toán 2: Lập phương trình chính tắc của elip ( E) đi qua điểm M và thỏa mãn điều kiện T ( về tiêu cự ; độ dài trục lớn- trục nhỏ; tâm sai....)

- Bước 1: Gọi phương trình chính tắc của elip( E) : 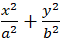= 1 (a > b > 0).

- Bước 2: Do điểm M thuộc elip (E) nên thạy tọa độ điểm này vào phương trình

( E) ta được một phương trình ẩn a²; b²

- Bước 3: Từ điều kiện T thiết lập một phương trình ẩn a ; b và c.

Mà a² – b² = c². Kết hợp ba phương trình trên để tìm a; b; c.

⇒ Phương trình chính tắc của elip ( E) .

B. Ví dụ minh họa

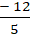
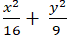
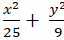
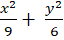
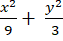
Ví dụ 1: Elip đi qua các điểm M ( 0; 3) và N( 3; ) có phương trình chính tắc là:

A. = 1     B. = 1

C. = 1     D. = 1

Lời giải

Gọi phương trình chính tắc của Elip là 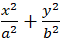= 1 (a > b > 0).

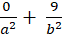
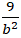
Elip đi qua điểm M( 0; 3) suy ra: = 1

⇔ = 1 ⇔ b² = 9 ( 1)

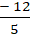
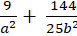
Elip đi qua điểm N N( 3; ) suy ra: = 1 ( 2)

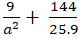
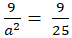
Thay( 1) vào ( 2) ta được: = 1

⇔ = 1 ⇔ a²= 25

Vậy phương trình cần tìm là: 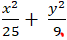= 1

Chọn B

Ví dụ 2: Tìm phương trình chính tắc của Elip có tiêu cự bằng 6 và đi qua điểm A( 0; 5).

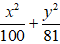
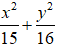
A. = 1     B. = 1

C. = 1     D. Đáp án khác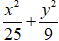

Lời giải

Gọi phương trình chính tắc của Elip có dạng 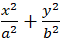= 1 (a > b > 0).

Ta có tiêu cự bằng 6 nên: 2c = 6 ⇒ c = 3 và a² - b² = c² = 9 ( 1)

Do điểm A(0; 5) thuộc ( E) nên:

= 1 ⇔ ⇔ b² = 25 mà b> 0 nên b= 5.

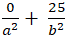
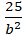
Thay vào (1) ta được : a² – 25 = 9 ⇔ a² = 34

⇒ Phương trình chính tắc của elip ( E) :     = 1

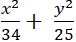
Chọn D

Ví dụ 3: Tìm phương trình chính tắc của Elip có trục lớn gấp đôi trục bé và đi qua điểm

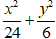
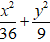
A. = 1     B. = 1

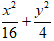
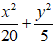
C. = 1     D. = 1

Lời giải

Gọi phương trình chính tắc của Elip có dạng 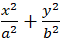= 1 (a > b > 0).

Theo đề ra: Trục lớn gấp đôi trục bé nên : 2a = 2.( 2b)

⇔ a = 2b ⇔ a² = 4b²

Điểm ( 2; -2) thuộc Elip : = 1 ⇔ = 1

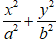
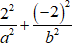
Ta được hệ: ⇒

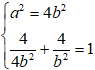
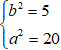
⇒ Phương trình elip ( E) :     = 1

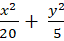
Chọn D

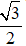
Ví dụ 4: Phương trình chính tắc của Elip có một tiêu điểm F₁(-√3; 0 ) và đi qua M(1; ) là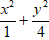

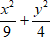
A. = 1     B. = 1

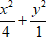
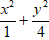
C. = 1     D. = 1

Lời giải

Do elip có một tiêu điểm là F1(- √3; 0) nên c = √3

Phương trình chính tắc của elip có dạng :

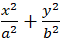
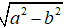
(E) : = 1 (a > b > 0) ⇒ c = = √3 ⇒ a² - b² = 3(1)

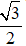
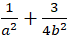
M(1; )∈ (E) ⇒ = 1 ⇔ 4b² + 3a² = 4a² b² (2)

Giải hệ (1) và (2)

⇔ ⇔ ⇔

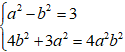
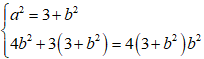
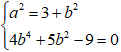
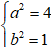
Vậy phương trình elip là:     = 1

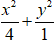
Chọn C

Ví dụ 5: Phương trình chính tắc của elip có hai tiêu điểm F1(- 2;0); F2(2; 0) và đi qua điểm M( 2; 3) là

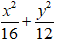
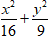
A. = 1     B. = 1

C. 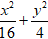= 1     D. Tất cả sai

Lời giải

+ Gọi phương trình chính tắc của elip cần tìm: 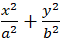= 1 (a > b > 0).

+ Ta có elip có hai tiêu điểm F1(- 2;0); F2(2; 0) nên c = 2

⇒ a²- b²=c² = 4 ⇒ a²= b² + 4 ( 1)

+ Do elip đi qua điểm M( 2; 3) nên :

= 1 ( 2)

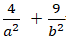
+ Từ (1) và (2) ta có hệ phương trình :

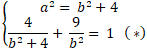
+ Giải phương trình ( *) ⇔ 4b² + 9( b²+ 4) = b² ( b² + 4)

⇔ 4b² + 9b²+ 36 = b⁴ + 4b²

⇔ b⁴ – 9b² -36 = 0 ⇔ b² = 12

⇒ a² = b² + 4 = 16

⇒ Phương trình chính tắc của elip ( E) :     = 1

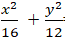
Chọn A

Ví dụ 6: Lập phương trình chính tắc của elip có tâm O; hai trục đối xứng là hai trục toạ độ và qua hai điểm ,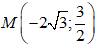

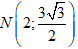
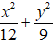
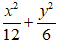
A. = 1     B. = 1

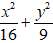
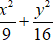
C. = 1     D. = 1

Lời giải

Gọi phương trình chính tắc elip cần tìm là 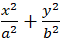= 1 (a > b > 0).

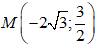
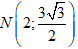
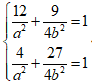
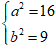
Do elip đi qua , nên ta có hệ :

⇔

Vậy elip cần tìm là     = 1

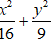
Chọn C

Ví dụ 7: Tìm phương trình chính tắc của elip nếu nó có chiều rộng hình chữ nhật cơ sở là 8 và đi qua A(5; 0) ?

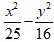
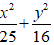
A. = 1     B. = 1

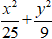
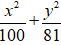
C. = 1     D. = 1

Lời giải

Gọi phương trình chính tắc của elip 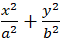= 1 (a > b > 0).

Do chiều rộng hình chữ nhật cơ sở là 8 nên 2b = 8 ⇔ b = 4

Do elip đi qua điểm A( 5;0) nên: 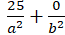= 1

⇔ a² = 25

Phương trình chính tắc của elip :     = 1

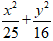
Chọn B

Ví dụ 8: Tìm phương trình chính tắc của elip nếu nó đi qua điểm A(6; 0) và tỉ số của tiêu cự với độ dài trục lớn bằng .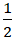

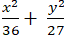
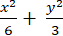
A. = 1     B. = 1

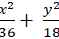
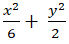
C. = 1     D. = 1

Lời giải

Gọi phương trình chính tắc của Elip là: 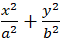= 1 (a > b > 0).

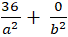
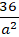
Elip đi qua điểm A( 6;0) suy ra: =1

⇔ =1 ⇔ a² = 36 mà a > 0 nên a = 6.

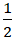
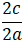
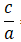
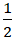
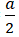
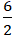
Tỉ số của tiêu cực với độ dài trục lớn bằng suy ra :

= = ⇒ c = = = 3

⇒ b² = a² – c² = 62 – 32= 27

Vậy phương trình cần tìm là ( E) :     = 1

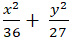
Chọn A

C. Bài tập vận dụng

Câu 1: Tìm phương trình chính tắc của elip nếu nó đi qua điểm A(2; 1) và có tiêu cự bằng 2√3 ?

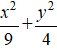
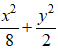
A. = 1     B. = 1

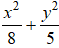
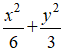
C. = 1     D. = 1

Lời giải:

Đáp án: D

Trả lời:

Giả sử elip có phương trình tổng quát là 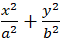= 1 (a > b > 0).

Do elip có tiêu cự là 2√3 nên 2c= 2√3 ⇔ c= √3.

Do ( E) đi qua điểm A(2; 1) và có tiêu cự bằng nên ta có

⇔

⇔ ⇔ ⇒

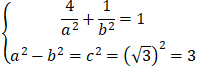
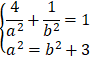
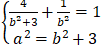
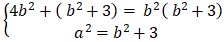
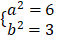
Vậy phương trình (E):    = 1

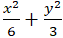
Câu 2: Tìm phương trình chính tắc của elip nếu nó đi qua điểm A( 6;0) và có tâm sai bằng 1/2

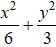
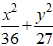
A. = 1     B. = 1

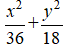
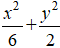
C. = 1     D. = 1

Lời giải:

Đáp án: B

Trả lời:

Giả sử elip có phương trình tổng quát là 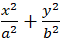= 1 (a > b > 0).

Do ( E) đi qua điểm A(6; 0) và có tâm sai bằng 1/2 nên ta có:

⇔

⇔ ⇔ ⇒ ( E ) : = 1

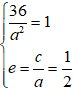
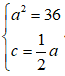
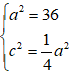
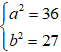
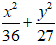
Câu 3: Lập phương trình chính tắc của elip có tiêu cự bằng 8 và đi qua M(√15 ; -1)

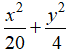
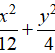
A. = 1     B. = 1

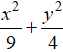
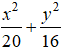
C. = 1     D. = 1

Lời giải:

Đáp án: A

Trả lời:

Giả sử elip có phương trình tổng quát là 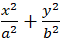= 1 (a > b > 0).

Do ( E) có tiêu cự bằng 8 và đi qua M(√15 ; -1) nên:

⇔

⇔ ⇔ ⇒

⇔ ⇒

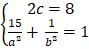
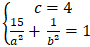
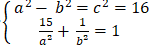
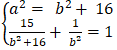
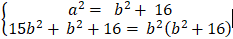
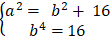
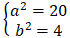
⇒ Phương trình chính tắc của elip(E):     = 1

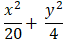
Câu 4: Tìm phương trình chính tắc của elip, biết elip có chiều dài hình chữ nhật cơ sở bằng 4√5 và đi qua điểm M( 0; -1)?

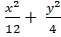
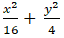
A. = 1     B. = 1

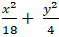
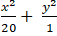
C. = 1     D. = 1

Lời giải:

Đáp án: D

Trả lời:

Gọi phương trình chính tắc của Elip là: 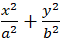= 1 (a > b > 0).

Elip có chiều dài hình chữ nhật cơ sở bằng 4√5 suy ra:

2a= 4 √5 nên a= 2√5 và a²= 20

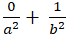
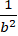
Elip đi qua điểm M(0; -1) suy ra: = 1 ( 2)

⇒ = 1 ⇒ b² = 1

Vậy phương trình cần tìm là:     = 1

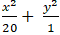
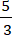
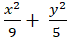
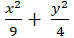
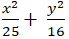
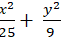
Câu 5: Elip qua điểm M(2; ) và có một tiêu điểm F( 2; 0) . Phương trình chính tắc của elip là:

A. = 1     B. = 1

C. = 1     D. = 1

Lời giải:

Đáp án: A

Trả lời:

Gọi phương trình chính tắc của Elip là: 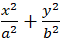= 1 (a > b > 0).

Elip có một tiêu điểm là F( 2; 0) suy ra c= 2 và c²= 4 ⇔ a²- b² = 4 (1).

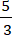
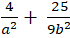
Elip đi qua điểm M(2; ) suy ra = 1 ( 2).

Từ (1) suy ra a²= b² + 4 thay vào (2) ta được :

= 1

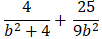
⇔ 36b² + 25( b² +4) = 9b² ( b² + 4)

⇔ 36b² + 25b² + 100 = 9b⁴ + 36b²

⇔ 9b⁴ – 25b² – 100 = 0

⇔ b² = 5 nên a² = b² + 4 = 9

Vậy phương trình cần tìm là ( E):     = 1

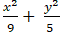
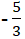
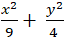
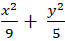
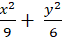
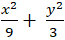
Câu 6: Tìm phương trình chính tắc của elip nếu nó đi qua điểm N(2; ) và tỉ số của tiêu cự với độ dài

A. = 1     B. = 1

C. = 1     D. = 1

Lời giải:

Đáp án: B

Trả lời:

Gọi phương trình chính tắc của Elip là: 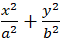= 1 (a > b > 0).

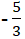
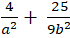
Elip đi qua điểm N( 2; ) suy ra: = 1 ( 1)

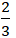
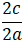
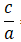
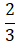
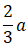
Tỉ số của tiêu cực với độ dài trục lớn bằng suy ra:

= = ⇒ c =

⇒ c²= .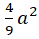

Kết hợp với điều kiện b² = a² – c² ta được :

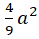
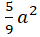
b² = a² - = hay 9b² = 5a² (2)

Thay ( 2) vào ( 1) ta được :

= 1 ⇔ = 1

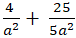
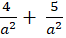
⇔a²= 9 ⇔ b² = 5

Vậy phương trình cần tìm là ( E):    = 1

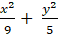
Câu 7: Tìm phương trình chính tắc của elip nếu nó đi qua điểm A(2; √3) và tỉ số của độ dài trục lớn với tiêu cự bằng .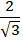

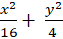
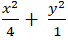
A. = 1     B. = 1

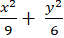
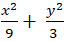
C. = 1     D. = 1

Lời giải:

Đáp án: A

Trả lời:

Gọi phương trình chính tắc của Elip là: 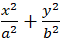= 1 (a > b > 0).

Elip đi qua điểm A( 2; √3) suy ra: 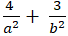=1 ( 1)

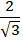
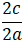
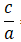
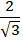
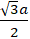
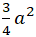
Tỉ số của độ dài trục lớn với tiêu cự bằng suy ra:

= = ⇒ c = và c² =

Kết hợp với điều kiện b² = a² - c² ta được :

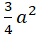
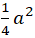
b² = a² - = nên a²= 4b² ( 2) .

Thay ( 2) vào (1) ta được : 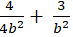= 1 ⇔ b² = 4

⇒ a² = 4b² = 16

Vậy phương trình cần tìm là:     = 1

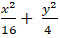
Câu 8: . Lập phương trình chính tắc của elip, biết elip đi qua hai điểm A( 7;0) và B(0; 3).

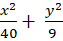
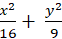
A. = 1     B. = 1

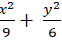
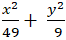
C. = 1     D. = 1

Lời giải:

Đáp án: D

Trả lời:

Gọi phương trình chính tắc của Elip là : 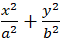= 1 (a > b > 0).

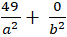
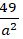
Elip đi qua điểm A( 7; 0) suy ra: = 1

⇔ = 1 ⇔ a²= 49.

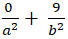
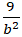
Elip đi qua điểm B(0; 3) suy ra: = 1

⇔ = 1 ⇔ b² = 9

Vậy phương trình cần tìm là :    = 1

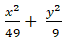
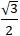
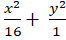
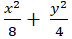
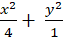
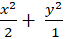
Câu 9: Elip đi qua các điểm A( 0; 1) và N( 1; ) có phương trình chính tắc là:

A. = 1     B. = 1

C. = 1     D. = 1

Lời giải:

Đáp án: C

Trả lời:

Gọi phương trình chính tắc của Elip là : 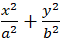= 1 (a > b > 0).

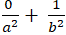
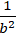
Elip đi qua điểm A( 0; 1) suy ra: = 1

⇔ =1 ⇔ b² = 1 ( 1)

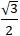
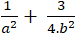
Elip đi qua điểm N( 1; ) suy ra: : = 1 ( 2)

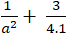
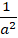
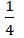
Thay( 1) vào ( 2) ta được: = 1

⇔ = ⇔ a²= 4

Vậy phương trình cần tìm là ( E) :    = 1