Cách tìm giao điểm của đường thẳng và Elip cực hay - Toán lớp 10

---

Cách tìm giao điểm của đường thẳng và Elip cực hay

Với Cách tìm giao điểm của đường thẳng và Elip cực hay Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm giao điểm của đường thẳng và Elip từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Phương pháp giải

+ Phương trình elip có dạng: 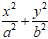= 1 và đường thẳng ∆: y = mx + n

+ Ta xét phương trình: 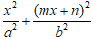= 1 (*) . Ta có 3 trường hợp:

TH1: (*) có 2 nghiệm thì số giao điểm là 2 (đường thẳng cắt elip).

TH2: (*) có 1 nghiệm thì số giao điểm là 1 (đường thẳng tiếp xúc elip).

TH3: (*) vô nghiệm thì số giao điểm là 0 (đường thẳng và elip không có điểm chung).

B. Ví dụ minh họa

Ví dụ 1: Cho elíp (E): 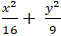= 1 và đường thẳng d: 3x + 4y - 12 = 0. Số giao điểm của đường thẳng d và elip (E) là:

A. 0    B. 1    C. 2    D. 3

Lời giải

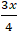
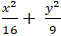
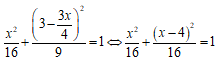
Ta có d: 3x + 4y - 12 = 0 nên y = 3 - , thay vào phương trình (E): = 1 ta được:

⇔ 2x² - 8x = 0

⇔

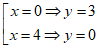
Vậy d luôn cắt (E) tại hai điểm phân biệt A(0; 3); B (4;0).

Chọn C.

Ví dụ 2: Cho elip (E): 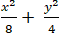= 1 và đường thẳng d: x - √2y + 2 = 0 . Số giao điểm của đường thẳng d và elip ( E) là:

A. 0    B. 1    C. 2    D. 3

Lời giải

Tọa độ giao điểm của elp (E) và d ( nếu có) là nghiệm của hệ:

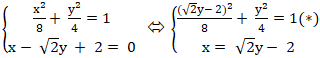
+ Giải (*) ta được: (√2 y - 2)² + 2y² = 8

⇔ 2y² - 4√2 y + 4 + 2y² = 8

⇔ 4y² - 4√2 y - 8 = 0

phương trình trên có hai nghiệm ⇒ cho ta 2 giá trị x tương ứng.

⇒ Số giao điểm của (E) và d là 2.

Chọn C.

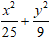
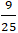
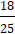
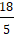
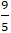
Ví dụ 3 : Cho Elip = 1 : . Đường thẳng (d): x = - 4 cắt (E) tại hai điểm M, N. Khi đó:

A. MN =    B. MN =    C. MN =    D. MN =

Hướng dẫn:

Elip (E) có a² = 25; b² = 9 ⇒ c² = 25 - 9 = 16 nên c = 4

Dể thấy (d): x = - 4 là đường thẳng đi qua tiêu điểm F1( - 4; 0) của ( E) .

Do đó MN = 2MF₁ =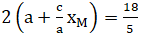

Chọn C.

Ví dụ 4: Đường thẳng y = kx cắt Elip 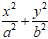= 1 (a > b > 0) tại hai điểm

A. đối xứng nhau qua trục Oy.    B. đối xứng nhau qua trục Ox.

C. đối xứng nhau qua gốc toạ độ O.    D. Các khẳng định trên đều sai.

Hướng dẫn

Vì (E) có tâm đối xứng là gốc tọa độ O và hàm số y = kx là hàm số lẻ nên đồ thị của nó cũng có tâm đối xứng là O(0; 0)

⇒ đường thẳng y = kx cắt elip tại hai điểm đối xứng với nhau qua gốc tọa độ O.

Chọn C.

Ví dụ 5: Cho elip 3x² + 4y² – 48 = 0 và đường thẳng d: x - 2y + 4 = 0. Giao điểm của d và Elip là :

A. (0; - 4); (-2; -3)    B. (4; 0); (3; 2)    C. (0; 4); (-2; 3)    D. (-4; 0); (2; 3)

Hướng dẫn giải

Xét hệ phương trình:

(*)

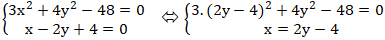
Giải (*): 3( 4y² – 16y + 16) + 4y² - 48 = 0

⇔ 12y² – 48y + 48 + 4y² - 48 = 0

⇔16y² – 48y = 0

⇔

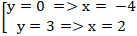
Vậy giao điểm của elip ( E) là ( - 4; 0) và ( 2; 3).

Chọn D.

Ví dụ 6: Tìm giao điểm của đường thẳng ( d): x - y - 3 = 0 và elip ( E): 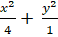= 1.

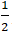
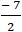
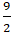
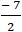
A. ( ; )    B. ( ; )    C. ( 10; 7)    D. ∅

Hướng dẫn giải

Xét hệ phương trình:

(*)

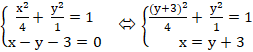
Giải ( *) ⇔ (y + 3)² + 4y² = 4 ⇔ y² + 9y + 9 + 4y² – 4 = 0

⇔ 5y² + 9y + 5 = 0 phương trình này vô nghiệm

Vậy đường thẳng d không cắt elip (E).

Chọn D.

Ví dụ 7: Tìm giao điểm của đường thẳng d: x + 2y - 5 = 0 và elip ( E): 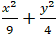= 1.

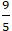
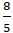
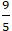
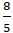
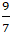
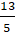
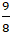
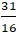
A. M( ; )    B. M( - ; - )    C. M( ; )    D. M( ; )

Lời giải

Xét hệ phương trình:

(*)

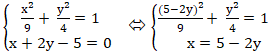
Giải phương trình ( *) ⇔ 4(5 - 2y)² + 9y² = 36

⇔ 100 - 80y + 16y² + 9y² = 36

⇔ 25y² – 80y + 64 = 0

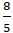
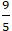
⇔ y = ⇒ x =

Vậy đường thẳng d cắt elip ( E) tại một điểm là M( ; )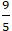

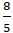
Chọn A.

C. Bài tập vận dụng

Câu 1: Tìm giao điểm ( nếu có ) của đường thẳng d: x - 2y = 0 và ( E): 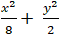= 1.

A. (2; 1)    B. ( - 2; -1) và ( -2; 1)    C. ( 2; 1) và ( -2; -1)    D. ( 2; -3) và ( 2; 1)

Lời giải:

Đáp án: C

Trả lời:

Xét hệ phương trình:

(*)

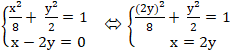
Giải phương trình ( *) ⇔ 4y² + 4y² = 8

⇔ 8y² = 8 ⇔ y² = 1

⇔

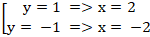
Vậy đường thẳng (d) cắt elip ( E) tại hai điểm A( 2; 1) và B( -2; -1).

Câu 2: Cho elip( E): 16x² + 25y² = 100. Tìm các giá trị của b để đường thẳng
(d): y = x + b có điểm chung với elip?

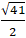
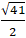
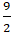
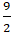
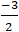
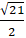
A. - ≤ b ≤    B. 2 < b < 3    C. - ≤ b ≤    D. ≤ b ≤

Lời giải:

Đáp án: A

Trả lời:

Đường thẳng (d): y = x + b có điểm chung với elip khi và chỉ khi hệ phương trình sau có nghiệm :

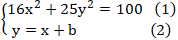
Thay ( 2) vào ( 1) ta được :

16x² + 25( x + b)² = 100 ⇔ 16x² + 25x² + 50bx + 25b² – 100 = 0

⇔ 41x² + 50bx + 25b² - 100 = 0 ( *)

Phương trình ( *) có nghiệm ⇔ ∆' ≥ 0

⇔ (25b)² – 41( 25b² - 100) ≥0

⇔ - 400b² + 4100 ≥0

⇔ - ≤ b ≤

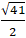
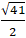
Câu 3: Cho elip ( E): 4x² + 9y² = 36 và M(1; 1). Lập phương trình đường thẳng qua M và cắt elip tại hai điểm A; B sao cho MA = MB?

A. x + 3y - 4 = 0    B. x - y = 0    C. 4x + 9y - 13 = 0    D. 2x - y - 1 = 0

Lời giải:

Đáp án: C

Trả lời:

+ Phương trình đường thẳng d: qua M(1; 1) ; hệ số góc k là:

(d): y = k( x - 1) + 1 ⇔ y = kx - k + 1

+ Tọa độ giao điểm của (d) và ( E) là nghiệm hệ phương trình :

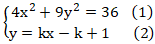
Thay ( 2) vào (1): 4x² + 9(kx - k + 1)² = 36

⇔ ( 4 + 9k²) x² – 18k( k - 1)x + 9k² - 18k - 27 = 0 ( *)

Để (d) cắt ( E) tại hai điểm thì phương trình (*) có hai nghiệm phân biệt ⇔ ∆' ≥ 0.

⇔ [ 9k(k - 1)]2 – (4 + 9k²) (9k² – 18k - 27) > 0

⇔ 9k² (k - 1)² – (4 + 9k²) ( k² - 2k - 3) > 0

⇔ 32k² + 8k + 12 > 0 luôn đúng với mọi k.

Vậy phương trình ( *) luôn có hai nghiệm phân biệt và x_A + x_B = 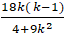( hệ thức Viet)

Theo giả thiết MA = MB ⇔ x_A + x_B = 2x_M

⇔ = 2 nên k =

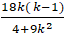
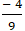
+ Thay k = 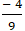vào (2) ta được: (d): 4x + 9y - 13 = 0

Câu 4: Cho elip 2x² + 3y² – 18 = 0 và đường thẳng d: 3x + y - 9 = 0. Giao điểm của d và Elip là :

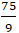
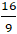
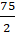
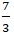
A. (-2; 9) và ( ; )    B. (4;- 9) và ( ; )

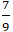
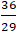
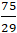
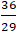
C. (0; 2) và ( ; )    D. (3; 0) và ( ; ) .

Lời giải:

Đáp án: D

Trả lời:

Xét hệ phương trình:

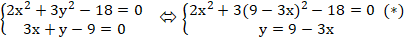
Giải (*): 2x² + 3( 81 - 54x + 9x²) – 18 = 0

⇔ 2x² + 243 - 162x + 27x² - 18 = 0

⇔ 29x² - 162x + 225 = 0

⇔

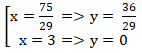
Vậy giao điểm của elip ( E) là (3; 0) và ( ; ) .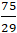

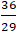
Câu 5: Tìm số giao điểm của đường thẳng ( d): x - 3y - 3 = 0 và elip ( E): 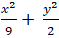= 1 có hoành độ nguyên?

A. 0    B. 1    C. 2    D. 3

Lời giải:

Đáp án: C

Trả lời:

Xét hệ phương trình:

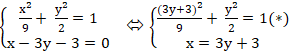
Giải ( *) ⇔ 2(3y + 3)² + 9y² = 18 ⇔ 18y² + 36y + 18 + 9y² – 18 = 0

⇔ 27y² + 36y = 0 ⇔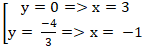

Vậy đường thẳng d cắt elip (E) tại hai điểm và hai điểm đó có hoành độ nguyên .

Câu 6: Tìm giao điểm của đường thẳng d: x + y - 10 = 0 và elip ( E): 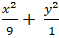= 1.

A. ∅    B. M( - ; - )    C. M( ; )    D. M( ; )

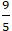
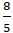
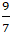
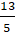
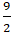
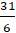
Lời giải:

Đáp án: A

Trả lời:

Xét hệ phương trình:

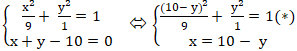
Giải phương trình ( *) ⇔ ( 10 - y)² + 9y² = 9

⇔ 100 – 20y + y² + 9y² = 9

⇔ 10y² - 20y + 91 = 0 phương trình vô nghiệm .

Vậy đường thẳng d không cắt elip ( E).

Câu 7: Đường thẳng d: x - 2y - 2 = 0 cắt elip ( E): 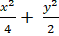= 1 tại hai điểm có hoành độ x₁; x₂. Tính x₁ + x₂

A. 0    B.    C. 2    D.

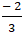
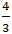
Lời giải:

Đáp án: D

Trả lời:

Xét hệ phương trình:

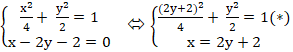
Giải phương trình ( *) ⇔ (2y + 2)² + 2y² = 4

⇔ 4y² + 8y + 4 + 2y² = 4 ⇔ 6y² + 8y = 0

⇔

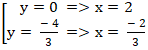
Vậy đường thẳng (d) cắt elip ( E) tại hai điểm A( 2; 0) và B( ; - ).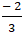

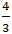
⇒ x₁ + x₂ = 2 + =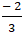

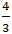
Câu 8: Cho elip( E): 4x² + 25y² = 100. Tìm các giá trị của b để đường thẳng
(d): y = 2x + b có điểm chung với elip?

A. -2√26 ≤ b ≤ 2√26    B. -√6 ≤ b ≤ √6

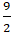
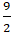
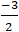
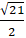
C. - ≤ b ≤    D. ≤ b ≤

Lời giải:

Đáp án: A

Trả lời:

Đường thẳng (d): y = 2x + b có điểm chung với elip khi và chỉ khi hệ phương trình sau có nghiệm :

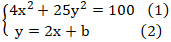
Thay ( 2) vào ( 1) ta được :

4x² + 25( 2x + b)² = 100 ⇔ 4x² + 100x² + 100bx + 25b² – 100 = 0

⇔ 104x² + 100bx + 25b² - 100 = 0 ( *)

Phương trình ( *) có nghiệm ⇔ ∆' ≥ 0

⇔ (50b)² – 104( 25b² - 100) ≥ 0

⇔ - 100b² + 10400 ≥ 0

⇔ - 2√26 ≤ b ≤ 2√26