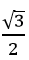Lý thuyết Giá trị lượng giác của một góc bất kì từ 0o đến 180o hay, chi tiết - Toán lớp 10

---

Lý thuyết Giá trị lượng giác của một góc bất kì từ 0o đến 180o hay, chi tiết

Tài liệu Lý thuyết Giá trị lượng giác của một góc bất kì từ 0o đến 180o hay, chi tiết Toán lớp 10 sẽ tóm tắt kiến thức trọng tâm về Giá trị lượng giác của một góc bất kì từ 0o đến 180o từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 10.

1. Định nghĩa

Với mỗi góc α (0^o ≤ α ≤ 180^o) ta xác định một điểm M trên nửa đường tròn đơn vị sao cho ∠ xOM = α và giả sử điểm M có tọa độ M(x^o, y^o).

Khi đó ta có định nghĩa:

sin của góc α là y^o, kí hiệu sinα = y^o;

cosin của góc α là x^o, kí hiệu cosα = x^o

tang của góc α là 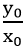(x^o ≠ 0),

kí hiệu tanα =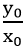

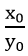
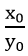
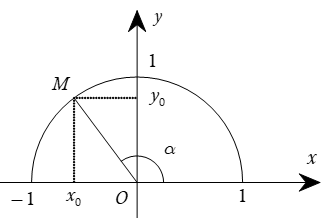
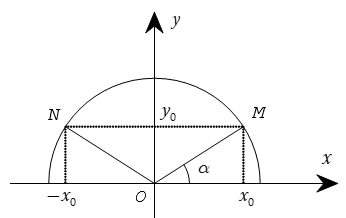
cotang của góc α là (y^o ≠ 0), kí hiệu cotα = .

2. Tính chất

Trên hình bên ta có dây cung NM song song với trục Ox và nếu ∠ xOM = α thì ∠xON = 180^o – α. Ta có yM = yN = y^o, xM = –xN = x^o. Do đó

sin α = sin(180^o – α)

cos α = –cos(180^o – α)

tan α = –tan(180^o – α)

cot α = –cot(180^o – α)

3. Giá trị lượng giác của các góc đặc biệt

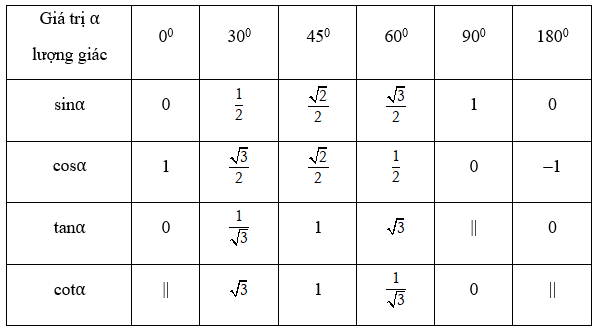
Trong bảng kí hiệu “||” để chỉ giá trị lượng giác không xác định.

Chú ý. Từ giá trị lượng giác của các góc đặc biệt đã cho trong bảng và tính chất trên, ta có thể suy ra giá trị lượng giác của một số góc đặc biệt khác.

Chẳng hạn:

sin 120^o = sin(180^o – 60^o) = sin60^o =

cos 135^o = cos(180^o – 45^o) = –cos45^o = -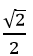

4. Góc giữa hai vectơ

a) Định nghĩa

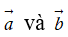
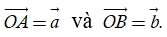
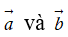
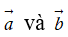
Cho hai vectơ đều khác vectơ 0 .Từ một điểm O bất kì ta vẽ Góc ∠AOB với số đo từ 0^o đến 180^o được gọi là góc giữa hai vectơ . Ta kí hiệu góc giữa hai vectơ là

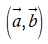
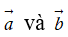
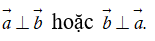
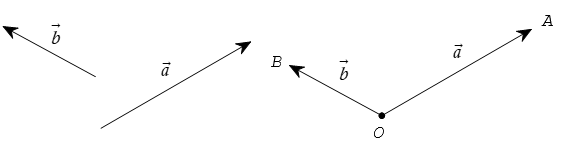
Nếu ( ) = 90^o thì ta nói rằng vuông góc với nhau, kí hiệu là

b) Chú ý. Từ định nghĩa ta có .