Xác định giá trị lượng giác của góc đặc biệt (bài tập + lời giải)

---

Haylamdo sưu tầm bài viết phương pháp giải bài tập Xác định giá trị lượng giác của góc đặc biệt lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Xác định giá trị lượng giác của góc đặc biệt.

Xác định giá trị lượng giác của góc đặc biệt (bài tập + lời giải)

1. Phương pháp giải

 +) Dựa vào định nghĩa, tìm tung độ y₀ và hoành độ x₀ của điểm M trên nửa đường tròn đơn vị với góc $\widehat{xOM}=\alpha$ và từ đó ta có các giá trị lượng giác:

$\sin \alpha =y_0; \cos \alpha =x_0; \tan \alpha =\frac{y_0}{x_0}; \cot \alpha =\frac{{\displaystyle x_0}}{{\displaystyle y_0}}$

+) Dựa vào tính chất: Hai góc bù nhau có sin bằng nhau và có côsin, tang, côtang đối nhau.

Với mọi góc α thỏa mãn 0° ≤ α ≤ 180°, ta luôn có:

sin(180° – α) = sinα;

cos(180° – α) = – cosα;

tan(180° – α) = – tanα (α ≠ 90°);

cot(180° – α) = – cotα (0° < α < 180°).

+) Sử dụng máy tính cầm tay.

2. Ví dụ minh họa

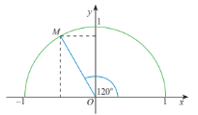
Ví dụ 1. Tìm các giá trị lượng giác của góc 120°.

Hướng dẫn giải:

Lấy điểm M trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=120°$.

Ta có: $\widehat{MOy}=120°-90°=30°$.

Ta tính được tọa độ điểm M: $\left\{\begin{array}{l}{x}_0=-\left(OM.\sin 30°\right)=-\left(1.\frac{1}{2}\right)=-\frac{1}{2}\\ y_0=OM.\cos 30°=1.\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}\end{array}\right.$.

Hay $M\left(-\frac{1}{2};\frac{\sqrt{3}}{2}\right)$.

Vậy theo định nghĩa ta có:

$\sin 120°=\frac{\sqrt{3}}{2};\cos 120°=-\frac{1}{2}$; $\tan 120°=-\sqrt{3};\cot 120°=-\frac{\sqrt{3}}{3}$.

Ví dụ 2. Cho góc α = 135°. Hãy tính sinα, cosα, tanα và cotα.

Hướng dẫn giải:

Ta có sin135° = sin(180° – 45°) = sin45° = $\frac{\sqrt{2}}{2}$;

cos135° = cos(180° – 45°) = – cos45° = -$\frac{\sqrt{2}}{2}$;

$\tan 135°=\frac{\sin 135°}{\cos 135°}=\frac{\frac{\sqrt{2}}{2}}{-\frac{\sqrt{2}}{2}}=-1$.

Do đó cot135° = $\frac{cos135°}{\sin 135°}=\frac{-\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}=-1$.

Ví dụ 3. Cho tam giác cân DEF có $\widehat{D}=\widehat{E}=15°$. Hãy tính các giá trị lượng giác của góc F.

Hướng dẫn giải:

Ta có $\widehat{F}=180°-\left(\widehat{D}+\widehat{E}\right)=180°-30°=150°$.

Do đó sinF = sin150° = sin(180° − 30°) = sin30° = $\frac{1}{2}$;

cosF = cos150° = cos(180° − 30°)= − cos30° = $-\frac{\sqrt{3}}{2}$;

tanF = $\frac{\sin 150°}{\cos 150°}=\frac{\frac{1}{2}}{-\frac{\sqrt{3}}{2}}=-\frac{\sqrt{3}}{3}$;

cotF = $\frac{cos150°}{\sin 150°}=\frac{-\frac{\sqrt{3}}{2}}{\frac{1}{2}}$= $-\sqrt{3}$.

3. Bài tập tự luyện

Bài 1. Cho góc α = 120°. Trong các khẳng định sau, khẳng định nào là SAI?

A. $\sin 120°=\frac{\sqrt{3}}{2}$;

B. $\cos 120°=-\frac{1}{2}$;

C. $\tan 120°=-\sqrt{3}$;

D. $\cot 120°=\sqrt{3}$.

Bài 2. Trong các đẳng thức sau đây, đẳng thức nào đúng?

A. sin60° = $\frac{\sqrt{3}}{2}$;

B. cos60° = $\frac{\sqrt{3}}{2}$;

C. tan60° = 1;

D. cot60° = −1.

Bài 3. Giá trị của tan135° bằng:

A. 1;

B. –1;

C. $\frac{1}{2}$;

D. -$\frac{1}{2}$.

Bài 4. Chọn phương án SAI trong các phương án dưới đây?

A. sin 0° = 0;

B. cos 90° = 0;

C. cos 0° = 1;

D. sin 90° = 0.

Bài 5. Cho $\widehat{A}=45°$, chọn đáp án SAI trong các đáp án dưới đây?

A. sin A = $\frac{\sqrt{3}}{2}$;

B. cos A = $\frac{\sqrt{2}}{2}$;

C. tan A = 1;

D. cot A = 1.

Bài 6. Cho biết sin α = $\frac{1}{2}$ và (180° – α) = $\frac{a}{b}$ (với $\frac{a}{b}$ là phân số tối giản). Tính a + b.

A. $\frac{1}{2}$;

B. -$\frac{1}{2}$;

C. 2;

D. 3.

Bài 7. Cho tam giác ABC vuông tại A có góc B bằng 60°. Tìm khẳng định đúng trong các khẳng định sau.

A. sin B = $\frac{1}{2}$;

B. cos B = $\frac{\sqrt{3}}{2}$;

C. cos C = $\frac{\sqrt{3}}{2}$;

D. sin C = $\frac{\sqrt{3}}{2}$.

Bài 8. Cho tam giác ABC cân tại A có $\widehat{A}=120°$. Khi đó sin B bằng:

A. $\frac{1}{2}$;

B. -$\frac{1}{2}$;

C. $\frac{\sqrt{3}}{2}$;

D. -$\frac{\sqrt{3}}{2}$.

Bài 9. Giá trị của biểu thức A = cos1°.cos2°.cos3°…cos89°.cos90° là:

A. 1;

B. 0;

C. –1;

D. 2.

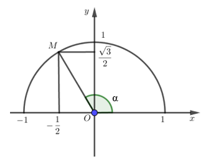
Bài 10. Cho góc α như hình vẽ, xác định giá trị của tan α.

A. tan α = $-\frac{\sqrt{3}}{3}$;

B. tan α = $-\frac{\sqrt{3}}{2}$;

C. tan α = $-\frac{2}{\sqrt{3}}$;

D. tan α = $-\sqrt{3}$.