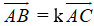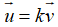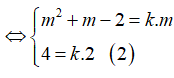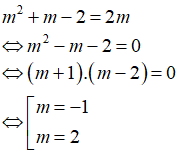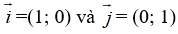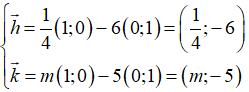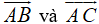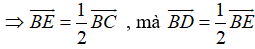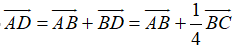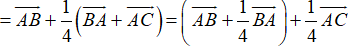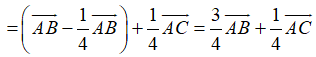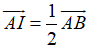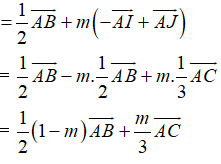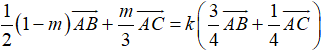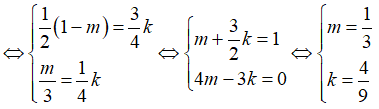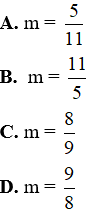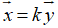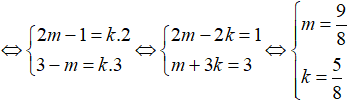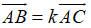Tìm m để hai vecto cùng phương cực hay, chi tiết - Toán lớp 10

---

Tìm m để hai vecto cùng phương cực hay, chi tiết

Với Tìm m để hai vecto cùng phương cực hay, chi tiết Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm m để hai vecto cùng phương từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Phương pháp giải

• Áp dụng điều kiện để hai vecto cùng phương để giải bài tập dạng này.

Điều kiện cần và đủ để hai vecto ( # 0) cùng phương là có một số k để .

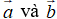
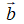
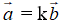
Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k khác 0 để

• Áp dụng trong hệ tọa độ:

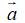
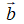
Cho = (a₁; a₂) và = (b₁; b₂), với b₁; b₂ # 0

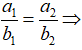
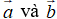
Khi đó nếu có: cùng phương.

B. Ví dụ minh họa

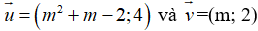
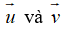
Ví dụ 1: Cho . Tìm m để hai vecto cùng phương.

Hướng dẫn giải:

Để hai vecto 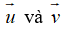cùng phương tồn tại số k thỏa mãn

Từ (2) suy ra k = 2 thay vào (1) ta được:

Vậy m = -1 và m = 2 thì hai vecto 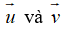cùng phương.

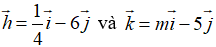
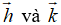
Ví dụ 2: Cho hai vecto . Tìm m để hai vecto cùng phương.

Hướng dẫn giải:

Ta có 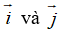là các vecto đơn vị với

Suy ra

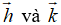
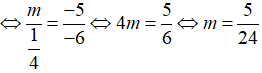
Hai vecto cùng phương

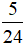
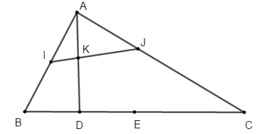
Vậy m = thì thỏa mãn yêu cầu bài toán.

Ví dụ 3: Cho tam giác ABC có E là trung điểm của BC, I là trung điểm của AB. Gọi D, J, K lần lượt là các điểm thỏa mãn 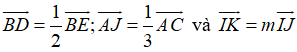. Tìm m để A, K, D thẳng hàng.

Hướng dẫn giải:

Ba điểm A, K, D thẳng hàng tồn tại k để (1)

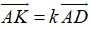
Ta phân tích các vecto 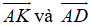theo hai vecto

+ E là trung điểm của BC

Suy ra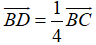

Ta có

Do đó 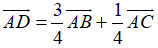(2)

+ Lại có: I là trung điểm AB

Ta có: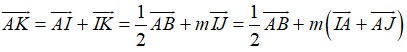

Do đó 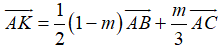(3)

Từ (1), (2) và (3) suy ra

Vậy m = 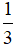thì ba điểm A, K, D thẳng hàng.

Ví dụ 4: Cho hai vecto 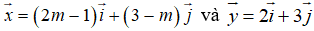. Giá trị của m để hai vecto cùng phương là:

Hướng dẫn giải:

Ta có và là các vecto đơn vị với

Suy ra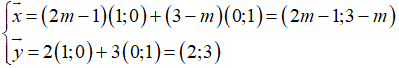

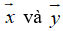
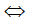
Hai vecto cùng phương tồn tại k để

Vậy m = .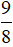

Đáp án D

Ví dụ 5: Trong mặt phẳng tọa độ Oxy, cho ba điểm A(m-1; 2); B(2; 5-2m) và C(m-3; 4). Giá trị của m để 3 điểm A, B, C thẳng hàng là

A. m = 3

B. m = 2

C. m = -2

D. m = 1

Hướng dẫn giải:

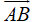
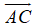
Ta có: = (2 - m + 1;5 -2m - 2) = (3 - m;3 - 2m)

= (m - 3 - m + 1;4 - 2) = (-2;2)

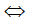
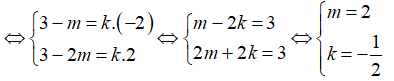
Ba điểm A, B, C thẳng hàng tồn tại k sao cho

Vậy m = 2 thì 3 điểm A, B, C thẳng hàng.

Đáp án B