Tìm tiêu điểm, tiêu cự, tâm sai, trục lớn, trục nhỏ của Elip - Toán lớp 10

---

Tìm tiêu điểm, tiêu cự, tâm sai, trục lớn, trục nhỏ của Elip

Với Tìm tiêu điểm, tiêu cự, tâm sai, trục lớn, trục nhỏ của Elip Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm tiêu điểm, tiêu cự, tâm sai, trục lớn, trục nhỏ của Elip từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Phương pháp giải

Cho elip (E): 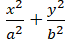= 1 ta có thể xác định được:

+ Các đỉnh : A₁(- a;0), A₂(a; 0), B₁( 0; - b), B₂(0; b)

+ Trục lớn : : A₁A₂ = 2a , trục nhỏ : B₁B₂ = 2b

+Hai tiêu điểm F₁(-c; 0); F₂(c; 0) với c² = a² - b²

+ Tâm sai e = 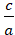< 1

+ Phương trình các đường thẳng chứa các cạnh của hình chữ nhật cơ sở là:

x = ± a; y = ±b.

B. Ví dụ minh họa

Ví dụ 1: Cho elip có phương trình: 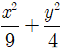= 1 Khi đó độ dài trục lớn, trục nhỏ lần lượt là.

A. 9; 4    B. 6; 4    C. 3; 2    D. 4; 6

Lời giải

Ta có: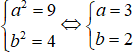

- Trục lớn: A₁ A₁ = 2a = 2.3 = 6

- Trục nhỏ: B₁ B₂ = 2b = 2.2 = 4

Chọn B

Ví dụ 2: Cho elip có phương trình: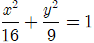 . Khi đó tọa độ tiêu điểm của elip là.

A. F₁ (-√7; 0), F₂ (√7; 0)     B. F₁ (-16; 0), F₂ (16; 0)

C. F₁ (-9; 0), F₂ (9; 0)     D. F₁ (-4; 0), F₂ (4; 0)

Lời giải

Ta có: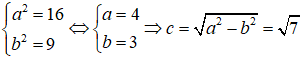

- Tiêu điểm là: F₁ (-√7;0), F₂ (√7;0)

Chọn A

Ví dụ 3: Cho elip có phương trình: 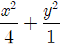= 1. Khi đó tọa độ hai đỉnh trên trục lớn của elip là.

A.A₁(-1; 0),A₁(1; 0)     B. A₁ (0; -1), A₁ (0; 1)

C.A₁(2; 0),A₁ (-1; 0)    D. A₁ (-2; 0), A₁ (2; 0)

Lời giải

Ta có: a² = 4 ⇔ a = 2

- Hai đỉnh trên trục lớn là: A₁ (-2; 0) , A₂ (2; 0)

Chọn D

Ví dụ 4: Cho elip có phương trình: 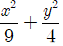= 1 . Khi đó tọa độ hai đỉnh trên trục nhỏ của elip là.

A. B₁(-2; 0), B₂(2; 0)     B. B₁( 0; 3) và B₂(0; 2).

C. B₁(-3; 0), B₂(-2; 0)     D. B₁( 0; -2) và B₂(0; 2).

Lời giải

Ta có: b² = 4 ⇔ b = 2

- Hai đỉnh trên trục nhỏ là: B₁( 0; -2) và    B₂(0; 2).

Chọn D

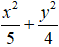
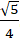
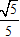
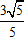
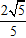
Ví dụ 5: Cho Elip = 1 . Tính tỉ số của tiêu cự với độ dài trục lớn của Elip.

A.           B.       C.       D.      

Hướng dẫn

Gọi phương trình chính tắc của Elip có dạng 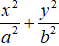= 1 ( a > b > 0 ).

Elip 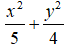= 1 có a² = 5, b² = 4 ⇒ c² = a²-b² = 1 ⇒ c = 1

Độ dài trục lớn: 2a = 2√5 ; tiêu cự 2c = 2.

Tỉ số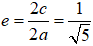

Chọn B.

Ví dụ 6: Đường Elip 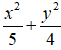= 1 có tiêu cự bằng

A. 2     B. 4     C. 9     D.1

Hướng dẫn giải

Ta có a² = 5; b² = 4

suy ra c = 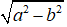= 1 .

Tiêu cự bằng: 2c = 2.

Chọn A.

Ví dụ 7: Cho Elip 9x² + 36y² – 144 = 0. Câu nào sau đây sai?

A. Trục lớn bằng 8.     B. Tiêu cự bằng 4√3

C. Tâm sai bằng 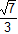    D. Trục nhỏ bằng 4

Hướng dẫn giải

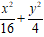
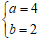
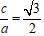
Ta có : 9x² + 36y² – 144 = 0 ⇔ = 1 ⇒ ⇒ x = 2√3 , e =

⇒ Trục lớn 2a = 8, trục nhỏ 2b = 4.

Tiêu cự 2c = 4√3 và tâm sai e = .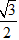

Chọn C.

Ví dụ 8: Cho Elip có phương trình : 9x² + 25y² = 225. Lúc đó hình chữ nhật cơ sở có diện tích bằng

A. 15;    B. 40    C. 60    D. 30

Hướng dẫn giải

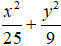
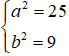
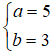
Ta có 9x² + 25y² = 225 ⇔ = 1 ⇒ ⇒

Độ dài trục lớn ( chiều dài hình chữ nhật cơ sở ): 2a = 10 .

Độ dài trục nhỏ ( chiều rộng hình chữ nhật cơ sở) 2b = 6 .

Diện tích hình chữ nhật cơ sở là: (2a). (2b) = 10.6 = 60

Chọn C.

Ví dụ 9 : Tâm sai của elip 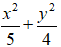= 1 bằng

A. 0,4;    B. 0, 2    C. D. 4

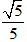
Hướng dẫn giải

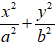
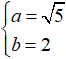
Từ dạng của elip = 1 ta có .

Từ công thức b² = a² - c² ⇒ c = 1 .

Tâm sai của elip e = c/a ⇒ e = = .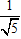

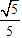
Chọn C.

Ví dụ 10: Cho elip ( E): 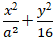= 1 với a> 0. Tìm a để elip (E) có tâm sai e= 3/5

A. 5     B. 6     C. 9     D. 4

Lời giải

+ Elip ( E): 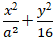= 1 có b²= 16 nên b= 4.

⇒ c²= a²- b² = a² - 16

⇒ c=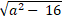

+ Tâm sai của elip ( E) là: e =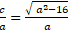

+ Theo đầu bài tâm sai e = 3/5 nên :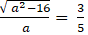

⇔ 5.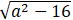 = 3a ⇔ 25( a² – 16) = 9a²

⇔ 25a² – 400 = 16a² ⇔ 16a² = 400

⇔ a² = 25 mà a> 0 nên a= 5.

Chọn A.

Ví dụ 11 : Cho elip ( E): 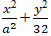= 1. Tìm b để elip (E) có chiều dài hình chữ nhật cơ sở là 20

A. 5     B. 6     C. 8     D. 10

Lời giải

+ Elip ( E): 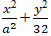= 1 có chiều dài hình chữ nhật cơ sở là 2a.

⇒Để chiều dài hình chữ nhật cơ sở là 20 thì: 2a= 20

⇔a= 10.

Chọn D.

Ví dụ 12 : Cho elip ( E): 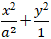= 1. Tìm a > 0 để tiêu cự của elip là 2√3?

A. 3    B. 4    C. 5       D. 2

Lời giải

+ Elip ( E): 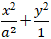= 1 có b²= 1

⇒ c²= a²- b² = a²- 1

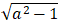
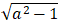
⇒ c = và tiêu cự của elip ( E) là: 2c= 2.

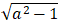
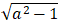
+ Để tiêu cự của elip là 2√3 thì: 2= 2√3

⇔ = √3 ⇔ a²- 1= 3

⇔ a²= 4 mà a> 0 nên a= 2

Chọn D.

Ví dụ 13: Cho elip ( E): 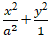= 1. Tìm a > 0 để diện tích hình chữ nhật cơ sở là 20.

A. 5     B. 4     C. 3        D. 10

Lời giải

Elip ( E) có b²= 1 nên b= 1.

Chiều dài hình chữ nhật cơ sở là : 2a.

Chiều rộng hình chữ nhật cơ sở là: 2b= 2.

⇒ Diện tích hình chữ nhật cơ sở là:

(2a) . ( 2b) = 2a. 2= 4a

Để diện tích hình chữ nhật cơ sở là 18 thì: 4a= 20 ⇔ a= 5.

Vậy a= 5.

Chọn A.

C. Bài tập vận dụng

Câu 1: Đường Elip 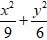= 1 có 1 tiêu điểm là

A. (0 ; 3)    B. (0 ; √6)    C. (-√3 ; 0)    D. (3 ; 0)

Lời giải:

Đáp án: C

Trả lời:

Ta có: a² = 9; b² = 6 nên c² = a² - b² = 3

⇒ c= √3

suy ra tiêu điểm F1(- √3;0) và F2(√3;0).

Câu 2: Đường Elip 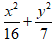= 1 có tiêu cự bằng

A. 18.    B. 6    C. 9    D. 3

Lời giải:

Đáp án: B

Trả lời:

Ta có: a² = 16; b² = 7 nên c² = a² – b² = 9

⇒ c = 3

suy ra tiêu cự là 2c = 6.

Câu 3: Cho Elip 4x² + 9y² - 36 = 0 . Khẳng định nào sau đây sai?

A. Trục nhỏ bằng 4    B. F₁(-√5; 0); F₂(-√5; 0)    C. e = 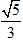   D. Trục lớn bằng 9

Lời giải:

Đáp án: D

Trả lời:

Ta đưa elip về dạng chính tắc 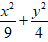= 1

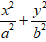
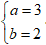
Từ dạng của elip = 1 ta có .

⇒ Độ dài trục lớn = 2a= 6 và độ dài trục bé 2b = 4.

Từ công thức b² = a² - c² ⇒ c = √5 ⇒ F₁(-√5 ; 0),F₂(-√5 ; 0) .

Tâm sai của elip e = ⇒ e =

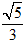
⇒ D sai.

Câu 4: Elip 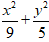= 1 có một tiêu điểm là

A. (0; √3).    B. (-2 ; 0)    C. (3 ; 0)    D. (0 ; 3)

Lời giải:

Đáp án: B

Trả lời:

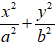
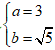
Từ dạng của elip = 1 ta có .

Từ công thức ⇒ c = 2 ⇒ F₁(-2 ; 0), F₂(0 ; 2) .

Câu 5:Elip 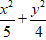= 1 có tiêu cự bằng

A. 2    B. 1    C. 4    D. 9

Lời giải:

Đáp án: A

Trả lời:

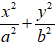
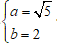
Từ dạng của elip = 1 ta có .

⇒ c² = a² - b² = 1 nên c = 1

⇒ Tiêu cự là 2c = 2;

Câu 6: Cho elip ( E): 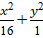= 1 có độ dài trục lớn là:

A. 2    B. 4    C. 8    D. 16

Lời giải:

Đáp án:C

Trả lời:

Elip ( E): 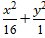= 1 có a² = 16 và b²= 1

⇒ a= 4 và b= 1

⇒ Độ dài trục bé là: 2a= 8

Câu 7:Cho elip ( E): 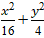= 1 có độ dài trục bé là:

A. 1    B. 2    C. 4    D. 8

Lời giải:

Đáp án: C

Trả lời:

Elip ( E): 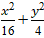= 1 có a² = 16 và b²= 4

⇒ a= 4 và b= 2

⇒ Độ dài trục bé là: 2b= 4

Câu 8:Elip 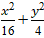= 1 có diện tích hình chữ nhật cơ sở là:

A. 16    B. 32    C. 9    D. 6

Lời giải:

Đáp án: B

Trả lời:

Từ dạng của elip 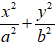= 1 ta có: a² = 16; b² = 4 .

⇒ a= 4 và b= 2

⇒ Chiều dài hình chữ nhật cơ sở là : 2a= 8

Chiều rộng hình chữ nhật cơ sở là: 2b = 4

⇒ Diện tích hình chữ nhật cơ sở là: 8.4 = 32.

Câu 9:Cho elip ( E): 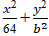= 1 với b> 0. Tìm b để elip (E) có diện tích hình chữ nhật cơ sở là 32.

A. 1    B. 2    C. 3    D. 4

Lời giải:

Đáp án: A

Trả lời:

Elip ( E): 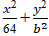= 1 có a²= 64 nên a= 8.

⇒ Chiều dài hình chữ nhật cơ sở là: 2a = 16.

Chiều rộng hình chữ nhật cơ sở là: 2b.

⇒ Diện tích hình chữ nhật cơ sở là: 16.2b = 32b.

Để diện tích hình chữ nhật cơ sở là 32 thì: 32b = 32 ⇔ b = 1.

Câu 10: : Elip 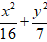= 1 có tâm sai bằng

A. 3    B. 1/2    C. 3/4    D. 1/8

Lời giải:

Đáp án: C

Trả lời:

Từ dạng của elip 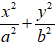= 1 ta có :

a² = 4; b² = 7 nên c² = 16- 7 = 9

⇒ a = 4; c = 3.

Tâm sai của elip .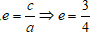

Câu 11:Cho Elip có phương trình : 4x²+ 9y² = 36 . Lúc đó hình chữ nhật cơ sở có diện tích bằng

A. 4    B. 6    C. 12    D. 24

Lời giải:

Đáp án: D

Trả lời:

Ta có 44x²+ 9y² = 36 ⇔ 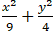= 1

⇒ a² = 9; b² = 4 nên a = 3; b = 2

Độ dài trục lớn ( chiều dài hình chữ nhật cơ sở ) : 2.a = 6

Độ dài trục nhỏ ( chiều rộng hình chữ nhật cơ sở): 2b = 4 .

Diện tích hình chữ nhật cơ sở là 6.4 = 24

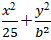
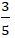
Câu 12: Cho elip ( E): = 1 với b > 0. Tìm b để elip (E) có tâm sai e = .

A. 1    B. 2    C. 3    D. 4

Lời giải:

Đáp án: D

Trả lời:

+ Elip ( E):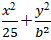

⇒ c²= a²- b² = 25- b²

⇒ c =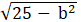

+ Tâm sai của elip ( E) là: e = =

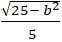
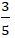
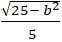
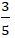
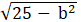
+ Theo đầu bài tâm sai e = nên : =

⇔ = 3 ⇔ 25 - b² = 9

⇔b² = 16 mà b > 0 nên b = 4.

Câu 13:Cho elip ( E): 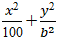= 1. Tìm b để elip (E) có chiều rộng hình chữ nhật cơ sở là 8

A. 1    B. 2    C. 3    D. 4

Lời giải:

Đáp án: D

Trả lời:

+ Elip ( E): 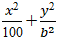= 1 có chiều rộng hình chữ nhật cơ sở là 2b

⇒Để chiều rộng hình chữ nhật cơ sở là 8 thì: 2b = 8

⇔ b = 4.

Câu 14:Cho elip ( E): 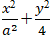= 1. Tìm a > 0 để tiêu cự của elip là 4√3?

A. 3    B. 4    C. 6    D. 8

Lời giải:

Đáp án: B

Trả lời:

+ Elip ( E): 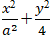= 1 có b² = 4

⇔ c² = a² - b² = a² - 4

⇔ c = √(a² -4) và tiêu cự của elip ( E) là: 2c = 2√(a² -4).

+ Để tiêu cự của elip là 4√3 thì: 2√(a² -4) = 4√3

⇔ √(a² -4) = 2√3 ⇔ a² - 4 = 12

⇔ a² = 16 mà a > 0 nên a = 4