Vị trí tương đối của hai đường tròn, của đường thẳng và đường tròn - Toán lớp 10

---

Vị trí tương đối của hai đường tròn, của đường thẳng và đường tròn

Với Vị trí tương đối của hai đường tròn, của đường thẳng và đường tròn Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Vị trí tương đối của hai đường tròn, của đường thẳng và đường tròn từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Phương pháp giải

+ Vị trí tương đối của hai đường tròn :

Cho hai đường tròn (C₁): tâm I₁; bán kính R₁ và đường tròn (C₂): Tâm I₂ bán kính R₂.

- Nếu I₁I₂ > R₁ + R₂ thì hai đường tròn không có điểm chung .

- Nếu I₁I₂ = R₁ + R₂ thì hai đường tròn tiếp xúc ngoài

- Nếu I₁I₂ = |R₁ - R₂ | thì hai đường tròn tiếp xúc trong.

- Nếu R₁ - R₂ < I₁I₂ < R₁ + R₂ thì hai đường tròn cắt nhau ( với R₁ > R₂) .

+ Vị trí tương đối của đường thẳng và đường tròn :

Cho đường thẳng d và đường tròn ( C): tâm I; bán kính R:

- Nếu d( I; d) = R thì đường thẳng tiếp xúc với đường tròn.

- Nếu d( I; d) > R thì đường thẳng và đường tròn không có điểm chung.

- Nếu d(I; d) < R thì đường thẳng và đường tròn cắt nhau tại hai điểm phân biệt.

B. Ví dụ minh họa

Ví dụ 1. Tìm giao điểm 2 đường tròn ( C₁) : x² + y² - 4 = 0 và
(C₂) : x² + y² - 4x - 4y + 4 = 0

A. (√2; √2) và (√2; - √2)    B. (0 ; 2) và (0 ; - 2)

C. (2 ; 0) và (0 ;2)    D. Đáp án khác

Hướng dẫn giải

Tọa độ giao điểm của 2đường tròn đã cho thỏa mãn hệ phương trình:

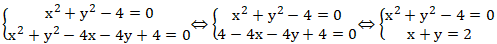
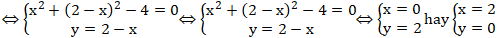
Vậy giao điểm A(0; 2) và B( 2; 0).

Chọn C.

Ví dụ 2 : Xác định vị trí tương đối giữa 2 đường tròn (C₁) : x² + y²= 4 và đường tròn
(C₂) : (x + 10)² + (y - 16)² = 1.

A. Cắt nhau.    B. Không cắt nhau.    C. Tiếp xúc ngoài.    D. Tiếp xúc trong.

Hướng dẫn giải

+ Đường tròn C₁ có tâm và bán kính: I₁ ( 0; 0) và R₁ = 2

+ Đường tròn ( C₂) có tâm và bán kính: I₂( - 10; 16) và R₂ = 1.

Khoảng cách giữa hai tâm I₁I₂ = = 2√89 > R₁ + R₂ .

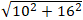
Vậy ( C₁) và ( C₂) không có điểm chung.

Chọn B.

Ví dụ 3: Tìm giao điểm 2 đường tròn (C₁) : x² + y² - 2 = 0 và (C₂) : x² + y² - 2x = 0

A. (2 ; 0) và (0 ; 2) .    B. (√2; 1) và (1; -√2) .

C. (1; - 1) và (1; 1)    D. ( - 1 ; 0) và (0 ; - 1) .

Hướng dẫn giải

Giao điểm nếu có của hai đường tròn đã cho là nghiệm hệ phương trình:

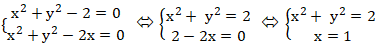
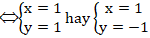
Vậy hai giao điểm là A( 1; 1) và B( 1; - 1) .

Chọn C.

Ví dụ 4: Tìm tọa độ giao điểm của đường thẳng ∆ : y = x và đường tròn
(C) : x² + y² - 2x = 0 .

A. ( 0; 0)    B. (0; 0) và (1;1) .    C. (2; 0)    D. (1;1)

Hướng dẫn giải

Giao điểm nếu có của đường thẳng ∆ và đường tròn ( C) là nghiệm hệ phương trình:

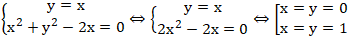
Vậy đường thẳng cắt đường tròn tại hai điểm là A( 0; 0) và B (1; 1).

Chọn B

Ví dụ 5 : Tọa độ giao điểm của đường tròn (C) : x² + y² - 2x - 2y + 1 = 0 và đường thẳng
∆ :

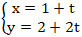
A. (1 ; 2) và ( 2 ;1)    B. (1 ;2) và ( ; ).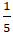

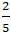
C. ( 2 ;5)    D. (1 ; 0) và (0 ;1)

Hướng dẫn giải

Thế 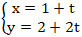vào (C) ta có:

( 1 + t)² + ( 2 + 2t)² - 2( 1 + t) - 2( 2 + 2t) + 1 = 0

⇔ 1 + 2t + t² + 4 + 8t + 4t² - 2 - 2t - 4 – 4t + 1 = 0

⇔ 5t² + 4t = 0

⇔

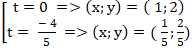
Chọn B

Ví dụ 6 : Xác định vị trí tương đối giữa 2 đường tròn ( C₁) : x² + y² = 4 và đường tròn
( C₂) : ( x - 3)² + ( y - 4)² = 25.

A. Không cắt nhau.    B. Cắt nhau.    C. Tiếp xúc ngoài.    D. Tiếp xúc trong.

Hướng dẫn giải

Đường tròn ( C₁) có tâm I₁( 0; 0) và bán kính R₁ = 2

Đường tròn ( C₂) có tâm I₂(3; 4) và bán kính R₂ = 5

Khoảng cách hai tâm I₁I₂ = 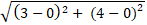= 5.

Ta có: R₂ - R₁ = 3 < I₁I₂ = 5 < R₂ + R₁ = 7 nên 2 đường tròn trên cắt nhau.

Chọn B.

Ví dụ 7 : Đường tròn x² + y² - 2x - 2y - 23 = 0 cắt đường thẳng d : x + y - 2 = 0 theo một dây cung có độ dài bằng bao nhiêu?

A. 10    B. 8    C. 6    D. 3√2.

Hướng dẫn giải

+ Đường tròn ( C) có tâm I( 1; 1) và bán kính R= 5.

+ Khoảng cách từ tâm I đến đường thẳng d là:

d(I,d) = 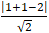= 0

⇒ điểm I thuộc đườngthẳng d nên đường thẳng ( d) cắt đường tròn ( C) tại hai điểm M và N trong đó MN là đường kính của đường tròn.

⇒ MN = 2R = 10

Vậy đường thẳng d cắt đường tròn( C) theo một dây cung có độ dài là 10.

Chọn A.

Ví dụ 8: Cho đương tròn C₁) có tâm I₁(1; 0); bán kính R₁ = 1 và đường tròn (C₂) có tâm I₂( - 5; 8), bán kính R₂ = 11. Xác định vị trí tương đối của hai đường tròn (C₁) và ( C₂)?

A. Tiếp xúc ngoài    B. Tiếp xúc trong

C. Cắt nhau    D. Không cắt nhau

Lời giải

+ Khoảng cách hai tâm là: I₁I₂ = = 10

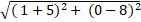
⇒ I₁I₂ = R₂ - R₁ = 10

⇒ Hai đương thẳng đã cho tiếp xúc trong.

Chọn B.

Ví dụ 9: Cho đương tròn C₁) có tâm I₁(2; - 3); bán kính R₁ = 3 và đường tròn (C₂) có tâm I₂(4; 7), bán kính R₂ = 6. Xác định vị trí tương đối của hai đường tròn (C₁) và ( C₂)?

A. Tiếp xúc ngoài    B. Tiếp xúc trong

C. Cắt nhau    D. Không cắt nhau

Lời giải

+ Khoảng cách hai tâm là: I₁I₂ = = √104

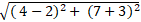
⇒ I₁I₂ > R₂ + R₁ = 9

⇒ Hai đường tròn đã cho không cắt nhau.

Chọn D.

Ví dụ 10. Cho đường tròn ( C): x² + y² – 2x + 4y = 0. Đường thẳng d: 2x - y + m = 0. Tìm m để đường thẳng d cắt đường tròn ?

A. – 7 < m < 1    B. - 9 ≤ m ≤ 1    C. - 9 < m < 1    D. - 9 < m ≤ 1

Lời giải

+ Đường tròn ( C) có tâm I ( 1; - 2) và bán kính R = = √5

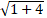
+ Khoảng cách từ tâm I đến đường thẳng d:

d(I; d) =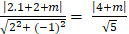

+ Để đường thẳng cắt đường tròn khi và chỉ khi đường thẳng và đường tròn tiếp xúc nhau hoặc cắt nhau nên:

d(I; d) ≤ R ⇔ 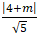≤ √5

⇔ |4 + m| ≤ 5

⇔ - 5 ≤ 4 + m ≤ 5 ⇔ - 9 ≤ m ≤ 1

Vậy để đường thẳng d cắt đường tròn khi - 9 ≤ m ≤ 1

Chọn B.

C. Bài tập vận dụng

Câu 1: Tìm giao điểm 2 đường tròn (C₁): x² + y² - 4 = 0 và
(C₂): x² + y² - 4x - 4y + 4 = 0

A. (√2; √2) và (√2; - √2) .    B. (0 ; 2) và (0 ; - 2)

C. (2 ; 0) và ( 0 ; 2)    D. (2 ; 0) và ( - 2 ;0)

Lời giải:

Đáp án: C

Trả lời:

Giao điểm của hai đường tròn đã cho là nghiệm hệ phương trình :

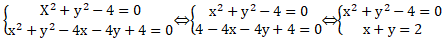
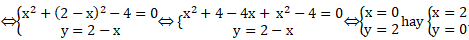
Vậy giao điểm A( 0; 2) và B( 2; 0)

Câu 2: Tìm toạ độ giao điểm hai đường tròn (C₁): x² + y² = 5 và
(C₂): x² + y² - 4x - 8y + 15 = 0

A. (1 ; 2) và (√2; √3) .    B. (1; 2) và ( - 2 ; 1)

C. (1 ; 2) và (√3; √2) .    D. (1;2).

Lời giải:

Đáp án: D

Trả lời:

Giao điểm nếu có của hai đường tròn đã cho là nghiệm hệ phương trình:

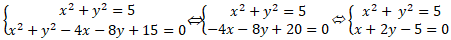
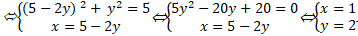
Vậy toạ độ giao điểm là ( 1; 2) .

Câu 3: Đường tròn ( C) : ( x - 2)² + ( y - 1)² = 25 không cắt đường thẳng nào trong các đường thẳng sau đây?

A. Đường thẳng đi qua điểm (2 ;6) và điểm ( - 1 ; 2)

B. Đường thẳng có phương trình y - 4 = 0.

C. Đường thẳng đi qua điểm ( 3 ; - 2) và điểm ( 19; 33) .

D. Đường thẳng có phương trình x - 8 = 0.

Lời giải:

Đáp án: D

Trả lời:

Đường tròn có tâm và bán kính là I( 2; 1) và bán kính R= 5.

Xét khoảng cách d từ tâm I đến từng đường thẳng và so sánh với R. Nếu d > R thì đường tròn không cắt đường thẳng

* Đường thẳng (a) đi qua điểm (2 ; 6) và điểm ( - 1 ;2) nhận u→( 3 ; 4) làm VTCP nên nhận n→( 4 ; - 3) làm VTPT

⇒ Phương trình ( a) : 4( x - 2) – 3( y - 6) = 0 hay 4x - 3y + 10 = 0

⇒ d( I ; a) = 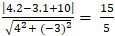= 3 < R

⇒ Đường tròn ( C) cắt đường thẳng này .

* ∆₂: y - 4 = 0 ⇒ khoảng cách d(I, ∆₂) = 3 < R ⇒ (C) cắt ∆₁

* Đường thẳng ( b) đi qua điểm (3 ; - 2) và điểm ( 19 ; 30) nhận VTCP u→(16 ; 32) nên nhận vTPT là n→( 2 ; - 1)

⇒ Phương trình ( b) : 2( x - 3) – 1(y + 2) = 0 hay 2x - y - 8 = 0

⇒ d( I ;b) = 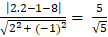= √5 < R

⇒ Đường tròn ( C) có căt đường thẳng (b).

*∆₄: x - 8 = 0 ⇒ khoảng cách d(I, ∆₄) = 6 < R ⇒ (C) không cắt ∆₄.

Câu 4: Tìm tọa độ giao điểm của đường thẳng ∆ : x - 2y + 3 = 0 và đường tròn
(C) : x² + y² - 2x - 4y = 0

A. (3; 3) và ( - 1; 1).    B. ( - 1; 1) và ( - 3; 3).    C. (3; 3) và (1; 2) .    D. (2 ; 1) và (2 ; - 1).

Lời giải:

Đáp án: A

Trả lời:

Tọa độ giao điểm là nghiệm của hệ phương trình sau

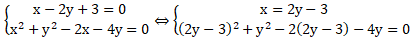
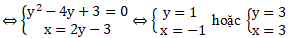
Vậy tọa độ giao điểm là (3; 3) và ( - 1 ; 1).

Câu 5: Xác định vị trí tương đối giữa 2 đường tròn (C₁) : x² + y² - 4x = 0 và
(C₂) : x² + y² + 8y = 0.

A. Tiếp xúc trong.    B. Không cắt nhau.    C. Cắt nhau.    D. Tiếp xúc ngoài.

Lời giải:

Đáp án: C

Trả lời:

Đường tròn (C₁): x² + y² - 4x = 0 có tâm I₁( 2; 0) và bán kính R₁ = 2.

Đường tròn (C₂) : x² + y² + 8y = 0 có tâm I₂( 0; - 4) , bán kính R₂ = 4.

Khoảng cách hai tâm : I₁I₂ = = 2√5

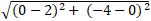
Ta có R₂ - R₁ < I₁I₂ = 2√5 < R₂ + R₁ nên hai đường tròn cắt nhau.

Câu 6: Tìm tọa độ giao điểm của đường thẳng ∆: x + y - 7 = 0 và đường tròn
(C): x² + y² - 25 = 0 .

A. (3 ;4) và ( - 4 ; 3).    B. (4 ; 3)    C. (3 ; 4)    D. (3; 4) và (4; 3).

Lời giải:

Đáp án: D

Trả lời:

Giao điểm nếu có của đường thẳng và đường tròn là nghiệm của hệ phương trình:

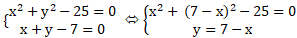
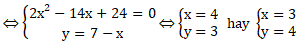
Vậy đường thẳng cắt đường tròn tại hai điểm là ( 4; 3) và ( 3; 4)

Câu 7: Đường tròn x² + y² - 4x + 6y - 12 = 0 cắt đường thẳng (d) : x - y - 3 = 0 theo một dây cung có độ dài bằng bao nhiêu?

A. 5    B. 2√23    C. 10    D. 5√2

Lời giải:

Đáp án: B

Trả lời:

+ Đường tròn ( C) có tâm I( 2; - 3) và bán kính R = 5.

+ Khoảng cách từ tâm I đến đường thẳng d là:

d(I, d) = 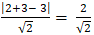= √2 < R

⇒ đường thẳng ( d) cắt đường tròn ( C) tại hai điểm M và N.

+ Gọi H là hình chiếu của I lên MN. Khi đó; H là trung điểm của MN ( quan hệ đường kính vuông góc với dây) .

+ Ta có IH = d(I, d) = √2

Áp dụng định lí Pytago vào tam giác MIH ta có

MI² = IH² + HM² ⇒ 5² = 2 + HM² ⇒ HM² = 23 nên HM= √23

Do H là trung điểm của MN nên MN = 2HM = 2√23

Câu 8: Đường tròn (C) : (x - 2)² + (y - 1)² = 25 không cắt đường thẳng nào trong các đường thẳng sau đây?

A. Đường thẳng đi qua điểm (2 ; 6) và điểm (45 ; 50) .

B. Đường thẳng có phương trình y - 4 = 0 .

C. Đường thẳng đi qua điểm (3 ; - 2) và điểm (19 ; 33)

D. Đường thẳng có phương trình x - 8 = 0.

Lời giải:

Đáp án: D

Trả lời:

Đường tròn có tâm và bán kính là: I(2; 1) và R = 5.

Xét khoảng cách d từ tâm I đến từng đường thẳng và so sánh với R:

* Đường thẳng đi qua điểm (2 ;6) và điểm (45 ; 50) : ∆₁: 44x - 43y + 170 = 0

⇒ khoảng cách d(I; ∆₁) = 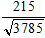< R nên (C) cắt ∆₁

* ∆₂ : y - 4 = 0 ⇒ khoảng cách d(I; ∆₂) = 3 < R nên (C) cắt ∆₂

* Đường thẳng đi qua điểm (3 ; - 2) và điểm (19 ; 33): ∆₃ : 35x - 16y - 137 = 0

⇒ khoảng cách d(I; ∆₁) = 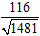< R ⇒ (C) cắt ∆₃

* ∆₄ : x - 8 = 0 ⇒ khoảng cách d(I; ∆₄) = 6 > R nên (C) không cắt ∆₄

Câu 9: Xác định vị trí tương đối giữa 2 đường tròn (C₁) : x² + y² = 4 và
(C₂) : (x + 10)² + (y - 16)² = 1.

A. Cắt nhau.    B. Không cắt nhau.    C. Tiếp xúc ngoài.    D. Tiếp xúc trong.

Lời giải:

Đáp án: B

Trả lời:

Đường tròn (C₁) có tâm và bán kính: I₁ = (0; 0) , và R₁ = 2; (C₂) có tâm I₂ ( - 10; 16) và bán kính R₂ = 1; khoảng cách giữa hai tâm I₁I₂ = = 2√89 > R₁ + R₂ .

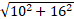
Vậy 2 đường tròn đã cho không có điểm chung.

Câu 10: Đường tròn nào dưới đây đi qua điểm A( 4; - 2)

A. x² + y² - 2x + 6y = 0.    B. x² + y² - 4x + 7y - 8 = 0.

C. x² + y² - 6x – 2y + 9 = 0.    D. x² + y² + 2x - 20 = 0.

Lời giải:

Đáp án: A

Trả lời:

Thế tọa độ của điểm A vào phương trình đường tròn x² + y² - 2x + 6y = 0. ta có:

4² + ( - 2)² - 2.4 + 6.( - 2) = 0

⇒ điểm A thuộc đường tròn.

Câu 11: Cho đương tròn C₁) có tâm I₁(3; 4); bán kính R₁ = 5 và đường tròn (C₂) có tâm I₂(7; 1), bán kính R₂ = 10. Xác định vị trí tương đối của hai đường tròn (C₁) và ( C₂)?

A. Tiếp xúc ngoài    B. Tiếp xúc trong

C. Cắt nhau    D. Không cắt nhau

Lời giải:

Đáp án: B

Trả lời:

+ Khoảng cách hai tâm là: I₁I₂ = 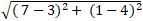= 5

⇒ I₁I₂ = R₂ - R₁ = 5

⇒ Hai đường thẳng đã cho tiếp xúc trong.