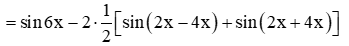Áp dụng công thức biến đổi tổng thành tích lớp 11 (bài tập + lời giải)

---

Haylamdo biên soan và sưu tầm trọn bộ chuyên đề phương pháp giải bài tập Áp dụng công thức biến đổi tổng thành tích lớp 11 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Áp dụng công thức biến đổi tổng thành tích.

Áp dụng công thức biến đổi tổng thành tích lớp 11 (bài tập + lời giải)

1. Phương pháp giải

Để làm tốt dạng bài này, ta cần nắm vững các công thức lượng giác đã học, đặc biệt là công thức biến đổi tổng thành tích.

Các công thức biến đổi tổng thành tích

$\cos a+\cos b=2\cos \frac{a+b}{2}.\cos \frac{a-b}{2}$

$\cos a-\cos b=-2\sin \frac{a+b}{2}.\sin \frac{a-b}{2}$

$\sin a+\sin b=2\sin \frac{a+b}{2}.\cos \frac{a-b}{2}$

$\sin a-\sin b=2\cos \frac{a+b}{2}.\sin \frac{a-b}{2}$

$\tan a+\tan b=\frac{\sin (a+b)}{\cos a.\cos b}$

$\tan a-\tan b=\frac{\sin (a-b)}{\cos a.\cos b}$

$\cot a+\cot b=\frac{\sin (a+b)}{\sin a.\sin b}$

$\cot a-\cot b=\frac{\sin (b-a)}{\sin a.\sin b}$.

2. Ví dụ minh họa

Ví dụ 1. Tính cos(−15°) + cos255°.

Hướng dẫn giải:

cos(−15°) + cos255° = $2\cos \frac{-15°+255°}{2}\cos \frac{-15°-255°}{2}$

$=2\cos 120°\cos \left(-135°\right)$

$=2\cdot \left(\frac{-1}{2}\right)\cdot \left(\frac{-\sqrt{2}}{2}\right)=\frac{\sqrt{2}}{2}$.

Ví dụ 2. Rút gọn biểu thức E = sin6x – 2sinx(cos3x + cos5x).

Hướng dẫn giải:

E = sin6x – 2sinx(cos3x + cos5x)

= $\sin 6x-2\sin x\left(2\cos \frac{3x+5x}{2}\cos \frac{3x-5x}{2}\right)$

= sin6x – 4sinxcos4xcosx

= sin6x – 2sin2xcos4x

= sin6x – (−sin2x + sin6x)

= sin2x.

3. Bài tập tự luyện

Bài 1. Trong các hệ thức sau, hệ thức nào sai?

A. sin10° + sin11° + sin15° + sin16° = 4sin13°cos2°30'cos0°30';

B. $\sin a+\sin 2a+\sin 3a+\sin 4a=4\sin a\sin \frac{5a}{2}cos\frac{a}{2}$;

C. $cosa+cos2a+cos3a+cos4a=4cosacos\frac{5a}{2}cos\frac{a}{2}$;

D. $1+\sin a+\cos a+\tan a=\frac{2\sqrt{2}{\text{cos}}^2\frac{a}{2}\sin \left(a+\frac{\pi }{4}\right)}{\cos a}$.

Bài 2. Viết biểu thức sin70° − sin20° + sin50° dưới dạng tích ta được kết quả là

A. 4cos10°cos35°cos65°;

B. 2cos10°cos35°cos65°;

C. 4cos10°sin35°cos65°;

D. 2cos10°sin35°cos65°.

Bài 3. Viết biểu thức cosa – cos5a dưới dạng tích ta được kết quả

A. 2sin6acos4a;

B. 2sin3acos2a;

C. 2sin3asin2a;

D. −2sin3asin2a.

Bài 4. Biến đổi thành tích biểu thức $\frac{\sin 7\alpha -\sin 5\alpha }{\sin 7\alpha +\sin 5\alpha }$ta được

A. tan5atana;

B. cosasina;

C. cos2asin3a;

D. cot6atana.

Bài 5. Biết $\tan x=\frac{1}{3}$. Tính giá trị của biểu thức $I=\frac{cos5x+cos3x}{\sin 5x-\sin 3x}$

A. $I=\frac{1}{3}$;

B. $I=-\frac{1}{3}$;

C. I = 3;

D. I = −3.

Bài 6. Rút gọn biểu thức $cos\left(x+\frac{\pi }{4}\right)-cos\left(x-\frac{\pi }{4}\right)$ta được

A. $\sqrt{2}\text{sinx}$;

B. $-\sqrt{2}\text{sinx}$;

C. $\sqrt{2}\text{cosx}$;

D. $-\sqrt{2}\text{cosx}$.

Bài 7. Rút gọn biểu thức P = cos(120° + x) + cos(120° − x) – cosx ta được kết quả là:

A. 0;

B. −cosx;

C. −2cosx;

D. sinx – cosx.

Bài 8. Biểu thức $\frac{\sin 10°+\sin 20°}{cos10°+cos20°}$bằng

A. tan10° + tan20°;

B. tan30°;

C. cot10° + cot20°;

D. tan15°.

Bài 9. Cho cos18° = cos78° + cosa°, giá trị dương nhỏ nhất của a là

A. 62;

B. 28;

C. 32;

D. 42.

Bài 10. Giá trị của $\frac{1}{\sin 18°}-\frac{1}{\sin 54°}$bằng

A. $\frac{1+\sqrt{2}}{2}$;

B.$\frac{1-\sqrt{2}}{2}$;

C. 2;

D. −2.