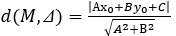Cách tìm ảnh của 1 đường thẳng qua phép tịnh tiến cực hay - Toán lớp 11

Cách tìm ảnh của 1 đường thẳng qua phép tịnh tiến cực hay

Với Cách tìm ảnh của 1 đường thẳng qua phép tịnh tiến cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm ảnh của 1 đường thẳng qua phép tịnh tiến từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

+) Sử dụng tính chất: d' là ảnh của d qua phép thì d' song song hoặc trùng với d

Nếu: d: Ax + By + C = 0; d'//d ⇒ d': Ax + By + C' = 0 (C' ≠ C)

+) Sử dụng biểu thức tọa độ

+) Chú ý: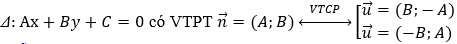

B. Ví dụ minh họa

Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho = (1;-3) và đường thẳng d có phương trình 2x - 3y + 5 = 0. Viết phương trình đường thẳng d' là ảnh của d qua phép tịnh tiến .

Hướng dẫn giải:

Cách 1. Sử dụng biểu thức tọa độ của phép tịnh tiến.

Lấy điểm M(x;y) tùy ý thuộc d, ta có 2x - 3y + 5 = 0 (*)

Cách 2. Sử dụng tính chất của phép tịnh tiến

Do d' = (d) nên d' song song hoặc trùng với d, vì vậy phương trình đường thẳng d' có dạng 2x - 3y + c = 0.(**)

Lấy điểm M(-1;1) ∈ d. Khi đó M' = (M) = (-1 + 1;1 - 3) = (0;-2).

Do M' ∈ d' ⇒ 2.0 - 3.(-2) + c = 0 ⇔ c = -6

Vậy ảnh của d là đường thẳng d': 2x - 3y - 6 = 0.

Cách 3. Để viết phương trình d' ta lấy hai điểm phân biệt M,N thuộc d, tìm tọa độ các ảnh M', N' tương ứng của chúng qua . Khi đó d' đi qua hai điểm M' và N'.

Cụ thể: Lấy M(-1;1), N(2;3) thuộc d, khi đó tọa độ các ảnh tương ứng là M'(0;-2), N'(3;0). Do d' đi qua hai điểm M', N' nên có phương trình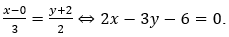

Ví dụ 2: Tìm PT đt d qua phép tịnh tiến theo : d biến thành d’, biết: d’: 2x + 3y – 1 = 0 với = (-2;-1)

Hướng dẫn giải:

* Cách 1: Gọi (d) = d'. Khi đó d // d’ nên PT đt d có dạng: 2x + 3y + C = 0

Chọn A’(2;-1) ∈ d’. Khi đó: (A) = A' ⇒ A(4; 0) ∈ d nên 8 + 0 + C = 0 ⇔ C = -8

Vậy: d: 2x + 3y – 8 = 0

* Cách 2: Chọn A’(2; -1) ∈ d’, (A) = A' ⇒ A(4; 0) ∈ d và chọn B’(-1;1) ∈ d’, (B) = B' ⇒ B(1;2) ∈ d

Đt d đi qua 2 điểm A, B nên PT đt d là:

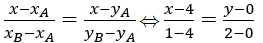
⇔ 2x – 8 = -3y

⇔ 2x + 3y – 8 = 0

* Cách 3: Gọi M’(x’;y’) ∈ d’, (M) = M'

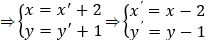
Ta có: M’ ∈ d’

⇔ 2x’ + 3y’ – 1 = 0

⇔ 2x – 4 + 3y – 3 – 1 = 0

⇔ 2x + 3y – 8 = 0

⇔ M ∈ d: 2x + 3y – 8 = 0

Ví dụ 3: Tìm tọa độ vectơ sao cho (d) = d' với d: 3x – y + 1 = 0 và d’: 3x – y – 7 = 0

Hướng dẫn giải:

d' là ảnh của d qua phép thì d' song song hoặc trùng với d

Nhận thấy d//d’ nên với mỗi điểm A ∈ d; B ∈ d' ta có:

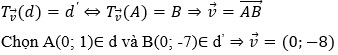
Ví dụ 4: Phép tịnh tiến theo vectơ = (3;m). Tìm m để đt d: 4x + 6y – 1 = 0 biến thành chính nó qua phép tịnh tiến theo vectơ

Hướng dẫn giải:

C. Bài tập trắc nghiệm

Câu 1. Trong mặt phẳng tọa độ Oxy cho đường thẳng Δ có phương trình 4x - y + 3 = 0. Ảnh của đường thẳng Δ qua phép tịnh tiến T theo vectơ = (2;-1) có phương trình là:

A. 4x - y + 5 = 0.

B. 4x - y + 10 = 0.

C. 4x - y - 6 = 0.

D. x - 4y - 6 = 0.

Lời giải:

.

Cách 1. Gọi Δ' là ảnh của Δ qua phép . Khi đó Δ' song song hoặc trùng với Δ nên Δ' có phương trình dạng 4x - y + c = 0.

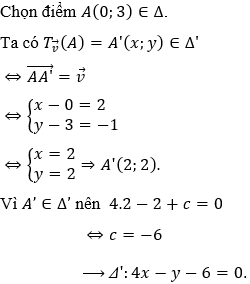
Chọn C.

Cách 2. Gọi M(x;y) là điểm bất kì thuộc đường thẳng Δ.

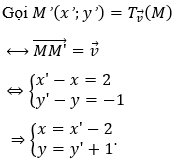
Thay x = x' - 2 và y = y' + 1 vào phương trình Δ ta được 4(x' - 2) - (y' + 1) + 3 = 0 ⇔ 4x' - y' - 6 = 0.

Câu 2. Trong mặt phẳng tọa độ Oxy nếu phép tịnh tiến biến điểm A(2;-1) thành điểm A'(1;2) thì nó biến đường thẳng d có phương trình 2x - y + 1 = 0 thành đường thẳng d' có phương trình nào sau đây?

A. d': 2x - y = 0.

B. d': 2x - y + 1 = 0.

C. d': 2x - y + 6 = 0.

D. d': 2x - y - 1 = 0.

Lời giải:

.

Gọi là vectơ thỏa mãn

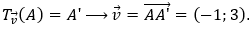
Ta có (d) = d' → d' song song hoặc trùng với d. Suy ra d': 2x - y + c = 0.

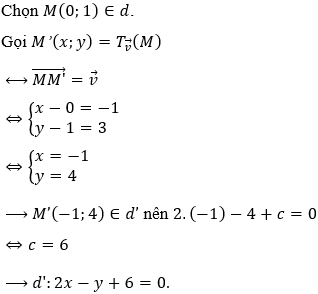
Chọn C.

Câu 3. Trong mặt phẳng tọa độ Oxy nếu phép tịnh tiến biến điểm A(2;-1) thành điểm A'(2018;2015) thì nó biến đường thẳng nào sau đây thành chính nó?

A. x + y - 1 = 0.

B. x - y - 100 = 0.

C. 2x + y - 4 = 0.

D. 2x - y - 1 = 0.

Lời giải:

.

• Gọi là vectơ thỏa mãn

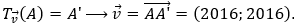
• Vì 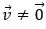nên qua phép tịnh tiến đường thẳng biến thành chính nó khi nó có vectơ chỉ phương cùng phương với

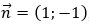
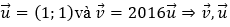
• Xét B, đường thẳng: x - y - 100 = 0 có một vectơ pháp tuyến , suy ra vectơ chỉ phương cùng phương.

Chọn B.

Câu 4. Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình 2x - y + 1 = 0. Để phép tịnh tiến theo vectơ biến d thành chính nó thì phải là vectơ nào trong các vectơ sau?

A. = (2;1).

B. = (2;-1).

C. = (1;2).

D. = (-1;2).

Lời giải:

.

Để d biến thành chính nó khi và chỉ khi vectơ cùng phương với vectơ chỉ phương của d.

Đường thẳng d có VTPT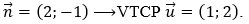

Chọn C.

Câu 5. Trong mặt phẳng tọa độ Oxy cho hai đường thẳng song song d và d' lần lượt có phương trình 2x - 3y - 1 = 0 và 2x - 3y + 5 = 0. Phép tịnh tiến nào sau đây không biến đường thẳng d thành đường thẳng d'?

A. = (0;2).

B. = (-3;0).

C. = (3;4).

D. = (-1;1).

Lời giải:

.

• Gọi = (a;b) là vectơ tịnh tiến biến đường d thành d'.

• Lấy M(x;y) ∈ d.

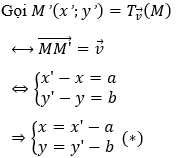
Thay (*) vào phương trình của d ta được 2(x' - a) - 3(y' - b) - 1 = 0 hay 2x' - 3y' - 2a + 3b - 1 = 0

suy ra phương trình d': 2x - 3y - 2a + 3b - 1 = 0

Mặt khác, theo giả thiết d': 2x - 3y + 5 = 0 ⇒ -2a + 3b - 1 = 5 (1)

Nhận thấy, = (-1;1) không thỏa mãn (1).

Chọn D.

Câu 6. Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng: d: 2x - y + 4 = 0 và d': 2x - y -1 = 0. Tìm giá trị thực của tham số m để phép tịnh tiến theo vectơ = (m;-3) biến đường thẳng d thành đường thẳng d’.

A. m = 1.

B. m = 2.

C. m = 3.

D. m = 4.

Lời giải:

.

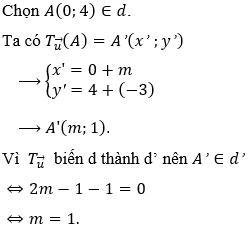
Chọn A.

Câu 7. Trong mặt phẳng tọa độ Oxy cho đường thẳng Δ có phương trình y = -3x + 2. Thực hiện liên tiếp hai phép tịnh tiến theo các vectơ 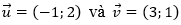thì đường thẳng Δ biến thành đường thẳng d có phương trình là:

A. y = - 3x + 1.

B. y = - 3x - 5.

C. y = - 3x + 9.

D. y = - 3x + 11.

Lời giải:

.

Từ giả thiết suy ra d là ảnh của Δ qua phép tịnh tiến theo vectơ .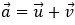

Ta có 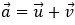= (2;3).

Biểu thức tọa độ của phép 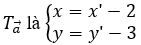thay vào Δ ta được:

y' - 3 = -3(x' - 2) + 2

↔ y' = -3x' + 11.

Chọn D.

Lưu ý: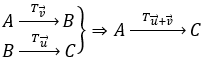

Câu 8. Trong mặt phẳng tọa độ Oxy cho đường thẳng Δ có phương trình 5x - y + 1 = 0. Thực hiện phép tịnh tiến theo phương của trục hoành về phía trái 2 đơn vị, sau đó tiếp tục thực hiện phép tịnh tiến theo phương của trục tung về phía trên 3 đơn vị, đường thẳng Δ biến thành đường thẳng Δ' có phương trình là

A. 5x - y + 14 = 0.

B. 5x - y - 7 = 0.

C. 5x - y + 5 = 0.

D. 5x - y - 12 = 0.

Lời giải:

.

+) Tịnh tiến theo phương trục hoành về phía trái 2 đơn vị tức là tịnh tiến theo vectơ .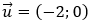

+) Tịnh tiến theo phương của trục tung về phía trên 3 đơn vị tức là tịnh tiến theo vectơ = (0;3).

+) Khi đó, ta thực hiện phép tịnh tiến theo vectơ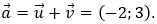

Ta có: 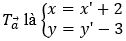thay vào Δ ta được 5(x' + 2) - (y' - 3) + 1 = 0 ⇔ 5x' - y' + 14 = 0.

Chọn A.

Câu 9. Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d: 2x - 3y + 3 = 0 và d': 2x - 3y - 5 = 0. Tìm tọa độ có phương vuông góc với d để .

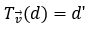
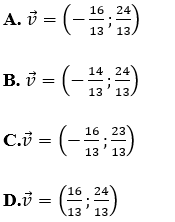
Lời giải:

.

Chọn A

Đặt = (a;b), lấy điểm M(x;y) tùy ý thuộc d, ta có d: 2x - 3y + 3 = 0 (*)

Gỉa sử M'(x';y') = (M). Ta có thay vào (*) ta được phương trình 2x' - 3y' - 2a + 3b + 3 = 0.

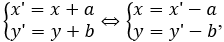
Từ giả thiết suy ra -2a + 3b + 3 = -5 ⇔ 2a - 3b = -8.

Vectơ pháp tuyến của đường thẳng d là .

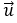
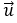
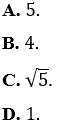
Câu 10. Trong mặt phẳng tọa độ Oxy cho hai đường thẳng có phương trình d: 3x - 4y + 5 = 0 và d’: 3x - 4y = 0. Phép tịnh tiến theo vectơ biến đường thẳng d thành đường thẳng d’. Khi đó, độ dài bé nhất của vectơ bằng bao nhiêu?

Lời giải:

.

+) Độ dài bé nhất của vectơ 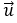bằng khoảng cách giữa hai đường d và d'.

+) Nhận thấy d//d’. Nên khoảng cách từ d đến d; bằng khoảng cách từ 1 điểm bất kì trên d đến d’ (hoặc từ 1 điểm bất kì trên d’ đến d)

+) Chọn A(0;0) ∈ d'. Ta có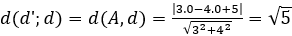

Chọn C.

Chú ý: Trong mặt phẳng Oxy cho M(x₀;y₀) và Δ: Ax + By + C = 0. Khi đó, khoảng cách từ M đến ∆ là: