Dạng bài Tính chất đối xứng trục hay, chi tiết - Toán lớp 11
Dạng bài Tính chất đối xứng trục hay, chi tiết
Với Dạng bài Tính chất đối xứng trục hay, chi tiết Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tính chất đối xứng trục từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải
[1]. Định nghĩa phép đối xứng trục.
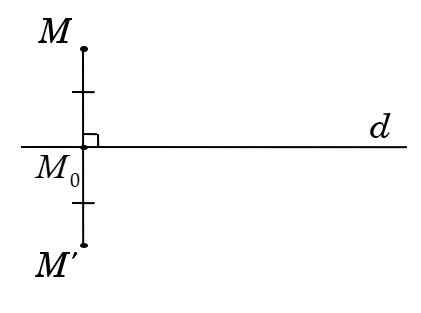
Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành M'sao cho d là đường trung trực của đoạn thẳng MM'được gọi là phép đối xứng qua đường thẳng d hay phép đối xứng trục d.
Đường thẳng d được gọi là trục của phép đối xứng hoặc đơn giản gọi là trục đối xứng.
Phép đối xứng trục d thường được kí hiệu là Dd.
Đường thẳng d được gọi là trục của phép đối xứng hoặc đơn giản gọi là trục đối xứng.
Phép đối xứng trục d thường được kí hiệu là Dd.
Nếu hình H' là ảnh của hình H qua phép đối xứng trục d thì ta còn nói H đối xứng với H' qua d, hay H và H' đối xứng với nhau qua d.
Nhận xét:
• Cho đường thẳng d. Với mỗi điểm M, gọi M0 là hình chiếu vuông góc của M trên đường thẳng d. Khi đó 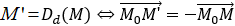
• 
[2]. Tính chất
Tính chất 1
Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.
Tính chất 2
Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
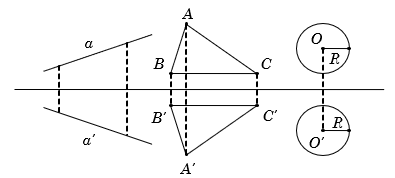
[3].Trục đối xứng của một hình
Định nghĩa
Đường thẳng d gọi là trục đối xứng của hình H nếu phép đối xứng qua d biến hình H thành chính nó.
Khi đó ta nói H là hình có trục đối xứng.
B. Ví dụ minh họa
Ví dụ 1: Cho góc nhọn xOy và điểm A thuộc miền trong của góc đó, điểm B thuộc cạnh Ox (B khác O). Tìm C thuộc Oy sao cho chu vi tam giác ABC nhỏ nhất?
Hướng dẫn giải:
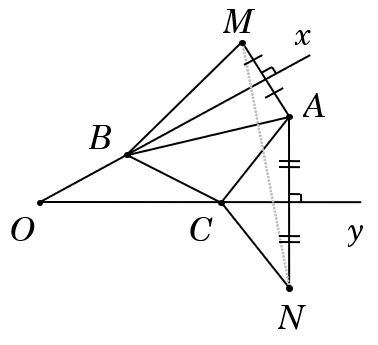
Gọi M là điểm đối xứng với A qua Ox. Vì B ∈ Ox nên suy ra BA = BM.
Gọi N là điểm đối xứng với A qua Oy Vì C ∈ Oy nên suy ra CA = CN.
Chu vi tam giác: PΔABC = AB + BC + CA = BM + BC + CN. (*)
Theo bất đẳng thức tam giác mở rộng, ta có
MB + BC ≥ MC và MC + CN ≥ MN.
Kết hợp với (*), suy ra
PΔABC = (MB + BC) + CN ≥ MC + CN ≥ MN.
Dấu "=" xảy ra khi và chỉ khi B, C, M, N thẳng hàng hay C là giao điểm của BM với trục Oy.
Ví dụ 2: Cho đường thẳng d và hai điểm A,B nằm cùng phía với d. Tìm điểm M trên d sao cho MA+MB đạt giá trị nhỏ nhất ?
Hướng dẫn giải:
- Tìm điểm A’ đối xứng với A qua d
- Nối A’B cắt d tại M. M chính là điểm cần tìm.
- Thật vậy: Vì A’ đối xứng với A qua d cho nên MA = MA’ (1). Do đó: MA + MB = MA’ + MB = A’B .
- Giả sử tồn tại M’ khác M thuộc d thì: M’A + M’B = M’A’ + M’B ≥ A'B. Dấu bằng chỉ xảy ra khi A’; M’; B thẳng hàng. Nghĩa là M trùng với M’.
Ví dụ 3: Cho đường thẳng d và hai điểm A,B (nằm về hai phía của d). Tìm điểm M trên d sao cho |MA - MB| đạt GTLN .
Hướng dẫn giải:
- Gọi A’ là điểm đối xứng với A qua d
- Nối A’B cắt d tại M. M chính là điểm cần tìm.
- Thật vậy: |MA - MB| = |MA' - MB| = A'B.
Giả sử tồn tại một điểm M’ khác với M trên d, khi đó: |M'A - M'B| = |M'A' - M'B| ≤ A'B. Dấu bằng chỉ xảy ra khi M’; A’; B thẳng hàng, nghĩa là M trùng với M’.

C. Bài tập trắc nghiệm
Câu 1. Tam giác đều có bao nhiêu trục đối xứng?
A. 0.
B. 1.
C. 3.
D. Vô số.
Lời giải:
.
Tam giác đều có 3 trục đối xứng (đường thẳng đi qua đỉnh tam giác và trung điểm cạnh đối diện).
Chọn C.
Câu 2. Trong các hình sau đây, hình nào có bốn trục đối xứng?
A. Hình bình hành.
B. Hình chữ nhật.
C. Hình thoi.
D. Hình vuông.
Lời giải:
.
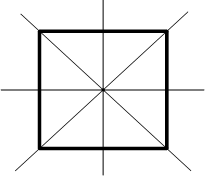
Hình vuông có bốn 4 trục đối xứng. (đường chéo và đường thẳng đi qua trung điểm của cặp cạnh đối diện).
Chọn D.
Câu 3. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Tam giác có trục đối xứng.
B. Tứ giác có trục đối xứng.
C. Hình thang có trục đối xứng.
D. Hình thang cân có trục đối xứng.
Lời giải:
.

Hình thang cân có trục đối xứng (đường thẳng đi qua trung điểm của hai cạnh đáy).
Chọn D.
Câu 4. Hình gồm hai đường tròn có tâm và bán kính khác nhau có bao nhiêu trục đối xứng?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
.
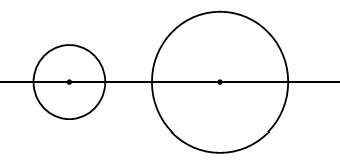
Có duy nhất một trục đối xứng đi qua tâm của hai đường tròn.
Chọn B.
Câu 5. Cho ba đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình H. Hỏi H có mấy trục đối xứng?
A. 0.
B. 1.
C. 2.
D. 3.
Lời giải:
.
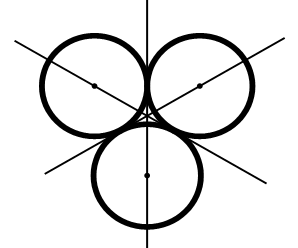
Có 3 trục đối xứng như hình vẽ.
Chọn D.
Câu 6. Có bao nhiêu phép đối xứng trục biến một đường thẳng d cho trước thành chính nó?
A. Không có phép nào.
B. Có một phép duy nhất.
C. Chỉ có hai phép.
D. Có vô số phép.
Lời giải:
.
Gọi Δ là đường thẳng vuông góc với đường thẳng d.
Khi đó, phép đối xứng trục Δ biến d thành chính nó.
Có vô số đường thẳng Δ vuông góc với d.
Chọn D.

Câu 7. Cho hai đường thẳng cắt nhau d và d'. Có bao nhiêu phép đối xứng trục biến d thành d'?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
.
Hai đường thẳng cắt nhau tạo ra 4 góc (2 cặp góc đối đỉnh bằng nhau).
Đường phân giác của 2 cặp góc đối đỉnh chính là 2 trục đối xứng biến d thành d'.
Chọn C.
Câu 8. Cho hai đường thẳng vuông góc với nhau a và b. Có bao nhiêu phép đối xứng trục biến a thành a và biến b thành b?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
.
Qua trục đối xứng là đường thẳng a sẽ biến a thành a và biến b thành b.
Qua trục đối xứng là đường thẳng b sẽ biến a thành a và biến b thành b.
Chọn C.
Câu 9. Hình gồm hai đường thẳng d và d' vuông góc với nhau có mấy trục đối xứng?
A. 0.
B. 2.
C. 4.
D. Vô số.
Lời giải:
.
Đây là trường hợp đặc biệt của Câu 7 và 8
Có 2 trục đối xứng là 2 đường phân giác của 2 cặp góc tạo bởi d và d'. Trường hợp này trục đối xứng biến d thành d' và d' thành d.
Có 2 trục đối xứng chính là d và d'. Trường hợp này, qua phép đối xứng trục biến d thành chính nó và d' thành chính nó.
Chọn C.
Câu 10. Cho hai đường thẳng a và b cắt nhau và góc ở giữa chúng bằng 60°. Có bao nhiêu phép đối xứng trục biến a thành a và biến b thành b?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
.
Để biến a thành a thì trục đối xứng trùng với a hoặc vuông góc với a.
TH1: Trục đối xứng trùng với a, mà a tạo với b góc 60° → a không là trục đối xứng để biến b thành b.
TH2: Trục đối xứng vuông góc với a, mà a tạo với b góc 60° → đường thẳng đó không là trục đối xứng để biến b thành b.
Chọn A.
Câu 11. Cho hai đường thẳng song song d và d'. Có bao nhiêu phép đối xứng trục biến mỗi đường thẳng thành chính nó ?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
.
Đường thẳng Δ vuông góc với d và d' sẽ biến d và d' thành chính nó.
Có vô số đường thẳng Δ vuông góc với d và d'.
Chọn D.
Trục đối xứng là đường thẳng song song và cách đều d và d'.
Câu 12. Cho hai đường thẳng song song a và b, một đường thẳng c vuông góc với chúng. Có bao nhiêu phép đối xứng trục biến mỗi đường thẳng đó thành chính nó?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
.
Để biến đường thẳng c thành chính nó thì trục đối xứng có dạng trùng với c hoặc vuông góc với c.
TH1: Trục đối xứng trùng với c → trục đối xứng vuông góc với a và b
⇒ trục đối xứng biến a và b thành chính nó. Do đó trường hợp này thỏa mãn.
TH2: Trục đối xứng vuông góc với c, tức là trục đối xứng song song (hoặc trùng) với a và b. Khi đó, trục đối xứng không thể biến a và b thành chính nó.
Vậy có duy nhất một phép đối xứng trục thỏa mãn bài toán.
Chọn B.
Câu 13. Cho hai đường thẳng song song a và b, một đường thẳng c vuông góc với chúng. Có bao nhiêu phép đối xứng trục biến a thành b và c thành chính nó?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
.
Để biến đường thẳng c thành chính nó thì trục đối xứng có dạng trùng với c hoặc vuông góc với c.
TH1: Trục đối xứng trùng với c → trục đối xứng vuông góc với a và b
⇒ trục đối xứng biến a và b thành chính nó. Do đó trường hợp này không thỏa mãn.
TH2: Trục đối xứng vuông góc với c, tức là trục đối xứng song song (hoặc trùng) với a và b. Khi đó, để trục đối xứng biến a thành b thì trục đối xứng phải cách đều a và b. Do đó trường hợp này có 1 trục đối xứng thỏa mãn.
Chọn B.

