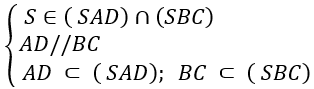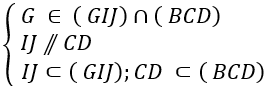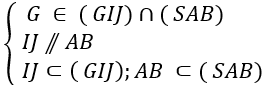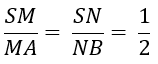Cách tìm giao tuyến của 2 mặt phẳng chứa 2 đường thẳng song song - Toán lớp 11

---

Cách tìm giao tuyến của 2 mặt phẳng chứa 2 đường thẳng song song

Với Cách tìm giao tuyến của 2 mặt phẳng chứa 2 đường thẳng song song Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm giao tuyến của 2 mặt phẳng chứa 2 đường thẳng song song từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

Hai mặt phẳng chứa hai đường thẳng song song thì giao tuyến của chúng song song với 2 đường thẳng đó:

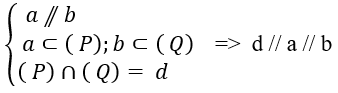
B. Ví dụ minh họa

Ví dụ 1: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của mp (SAD) và (SBC). Tìm mệnh đề đúng

A. d qua S và song song với BC

B. d qua S và song song với DC

C. d qua S và song song với AB

D. d qua S và song song với BD

Lời giải

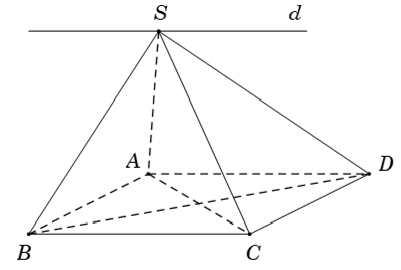
Ta có:

⇒ (SAD) ∩ (SBC) = Sx // AD // BC

Khi đó; đường thẳng d cần tìm chính là đường thẳng Sx.

Chọn A.

Ví dụ 2: Cho tứ diện ABCD. Gọi I và J theo thứ tự là trung điểm của AD và AC. Gọi G là trọng tâm tam giác BCD. Giao tuyến của 2 mặt phẳng (GIJ) và (BCD) là đường thẳng:

A. Qua I và song song với AB

B. Qua J và song song với BD

C. Qua G và song song với CD

D. Qua G và song song với BC

Lời giải

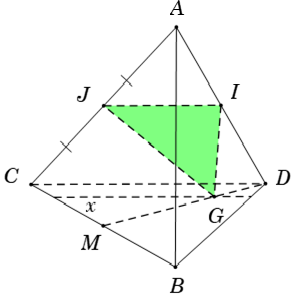
Ta có:

⇒ (GIJ) ∩ (BCD) = Gx // IJ // CD

Chọn C

Ví dụ 3: Cho hình chóp S. ABCD có đáy là hình thang với các cạnh đáy là AB và CD. Gọi I và J lần lượt là trung điểm AD và BC. Gọi G là trọng tâm tam giác SAB. Giao tuyến của mp(SAB) và mp(IJG) là:

A. SC

B. Đường thẳng qua S và song song với AB

C. Đường thẳng qua G và song song với CD

D. Đường thẳng qua G và cắt BC.

Lời giải

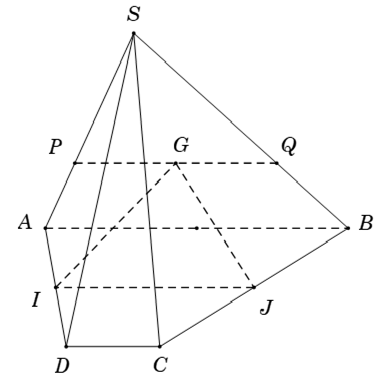
   + Xét hình thang ABCD có: I và J lần lượt là trung điểm của AD và BC

⇒ IJ là đường trunh bình của hình thang

⇒ IJ // AB // CD

Ta có:

⇒ (GIJ) ∩ (SAB) = Gx // IJ // AB

Chọn C

Ví dụ 4: Cho hình chóp S. ABCD có đáy ABCD là hình thang với đáy lớn AB đáy nhỏ CD. Gọi M; N lần lượt là trung điểm của SA và SB. Gọi P là giao điểm của SC và mp(AND). Gọi I là giao điểm của AM và DP. Hỏi tứ giác SABI là hình gì?

A. Hình bình hành

B. Hình chữ nhật

C. Hình vuông

D. Hình thoi

Lời giải

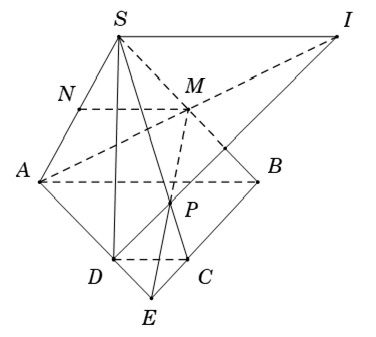
   + Gọi E là giao điềm của AD và BC; P là giao điểm của NE và SC

Suy ra: P = SC ∩ (AND)

   + Ta có

S là điểm chung thứ nhất của hai mặt phẳng (SAB) và (SCD)

Gọi I là giao điểm của DP và AN nên I là điểm chugn thứ hai của hai mặt phẳng (SAB) và (SCD)

Suy ra: SI = (SAB) ∩ (SCD)

Mà AB // CD nên SI // AB // CD

   + Vì MN là đường trung bình của tam giác SAB và chứng minh được cũng là đường trung bình của tam giác SAI nên suy ra: SI = AB (= 2 MN)

   + Tứ giác SABI có 2 cạnh đối SI và AB song song và bằng nhau nên SABI là hình bình hành.

Chọn A

Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của mặt phẳng (MCD) và (SAB) với M là một điểm bất kì thuộc cạnh SA.

A. Qua M và song song với AD

B. Qua M và song song với AB

C. Qua M và song song với AC

D. Qua M và song song với BD

Lời giải

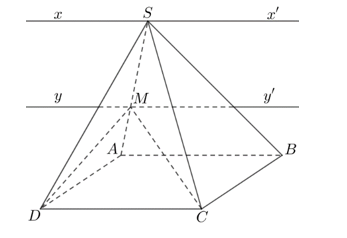
Ta có: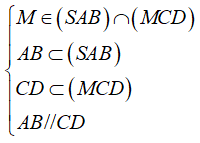

⇒ (SAB) ∩ (SCD) = yy', với yy' // AB // CD và M ∈ yy'

Chọn B

Ví dụ 6: Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Gọi O là giao điểm của AC và BD. Gọi H và M lần lượt là trung điểm của CD và AH. Tìm giao tuyến của (SMO) và (SCD)

A. Qua A và song song HC

B. Qua H và song song MO

C. Qua S và song song MO

D. Qua O và song song HC

Lời giải

   + Xét mp (ABCD) có M và O lần lượt là trung điểm của AH và AC

⇒ MO là đường trung bình của tam giác ACH.

⇒ MO // HC

   + Xét giao tuyến của hai mp (SMO) và (SHC) có:

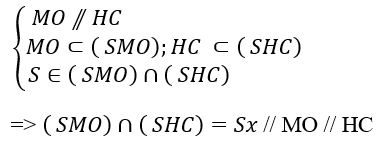
Chọn C

Ví dụ 7: Cho tứ diện ABCD. Gọi H là điểm bất kì trong mp (BCD); giao điểm của BH và CD là K. Trên cạnh BC lấy điểm M sao cho: BM/MC = BH/HK. Tìm giao tuyến của 2 mp (MHC) và (AKC)?

A. Qua A và song song MH

B. Qua C và song song HK

C. Qua C và song song MK

D. Qua C và song song MH

Lời giải

   + Xét tam giác ABK có: BM/MC = BH/HK

⇒ MH // AK (định lí Ta-let đảo)

   + Xét giao tuyến của hai mp(MHC) và (AKC) có:

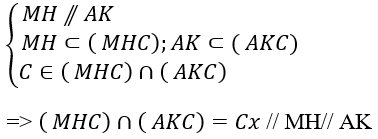
Chọn D

Ví dụ 8: Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Trên đoạn SA lấy điểm M sao cho 2SM = MA; trên đoạn SB lấy điểm N sao cho 2SN = NB. Điểm P nằm trên cạnh SC không trùng với S. Tìm giao tuyến của hai mp(MNP) và mp(SCD)?

A. Qua A và song song AB

B. Qua N và song song CD.

C. Qua P và song song CD.

D. Đáp án khác

Lời giải

   + Ta có: 2SM = MA và 2SN = NB nên:

⇒ MN // AB ( định lí Ta-let đảo)   (1)

   + Lại có ABCD là hình thoi nên AB // CD     (2)

Từ (1) và (2) suy ra: MN // CD.

   + Giao tuyến của mp(MNP) và (SCD):

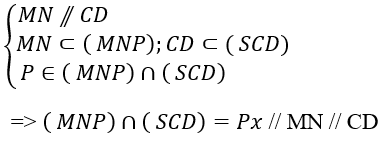
Chọn C

Ví dụ 9: Cho tứ diện ABCD và ba điểm P; Q: R lần lượt trên cạnh AB; CD và BC. Biết rằng PR // AC. Xác định giao điểm S của mp(PQR) và cạnh AD.

A. Là giao điểm của đường thẳng Qx và AD với Qx // AC

B. Là giao điểm của đường thẳng Px và AD với Px // BD

C. Là giao điểm của đường thẳng Rx và AD với Rx // BD

D. Là giao điểm của đường thẳng Qx và AD với Qx // BD

Lời giải

   + Chọn mặt phẳng phụ chứa AD là mp(ACD).

   + Xét giao tuyến của (ACD) và mp(PQR):

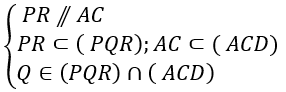
⇒ (PQR) ∩ (ACD) = Qx // PR // AC

   + Trong mp (ACD); Qx cắt AD tại S ta được điểm S cần tìm.

C. Bài tập trắc nghiệm

Câu 1: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)

A. là đường thẳng đi qua S song song với AB, CD

B. là đường thẳng đi qua S

C. là điểm S

D. là mặt phẳng (SAD)

Lời giải:

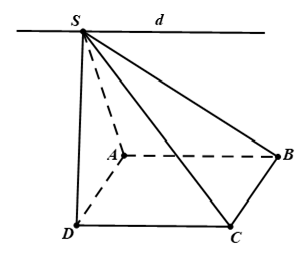
Ta có

⇒ (SAB) ∩ (SCD) = d // AB // CD, S ∈ d

Chọn A

Câu 2: Cho hình bình hành ABCD và một điểm S không nằm trong mặt phẳng (ABCD). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là một đường thẳng song song với đường thẳng nào sau đây?

A. AB       B. AC      C. BC      D. SA

Lời giải:

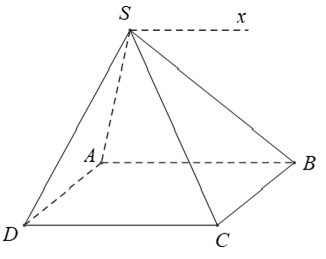
Chọn A

Xét (SAB) và (SCD) có S là điềm chung và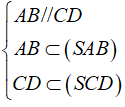

⇒ (SAB) ∩ (SCD) = Sx // AB // CD

Câu 3: Cho tứ diện ABCD. Gọi I và J theo thứ tự là trung điểm của AD và AC, G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GIJ) và (BCD) là đường thẳng

A. qua I và song song với AB

B. qua J và song song với BD

C. qua G và song song với CD

D. qua G và song song với BC

Lời giải:

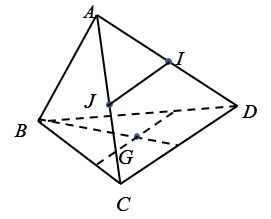
Chọn C

Gọi d là giao tuyến của (GIJ) và (BCD)

   + Do I và J lần lượt là trung điểm của AD và AC nên IJ là đường trung bình của tam giác ACD

⇒ IJ // CD.

   + Xét hai mp(GIJ) và mp (BCD):

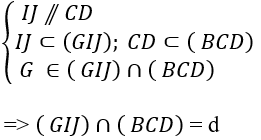
trong đó d qua G và d // CD // IJ

Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M là điểm bất kì thuộc đoạn thẳng SD. Chọn mệnh đề sai?

A. Giao tuyến của (SAB) và (SCD) là đường thẳng qua S và song song với AB

B. Giao tuyến của (SCD) và (MAB) là đường thẳng qua M và song song với CD.

D. Giao tuyến của (SCD) và (MAB) song song với giao tuyến của (SAB) và (SCD)

D. A và B đúng ; C sai.

Lời giải:

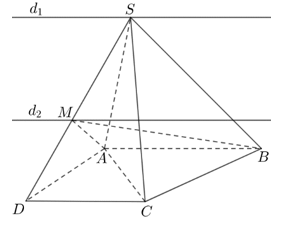
   + Ta tìm giao tuyến của mp (SAB) và (SCD):

Ta có: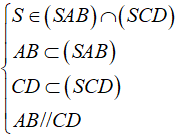

⇒ (SAB) ∩ (SCD) = d₁, với S ∈ d₁ và d₁ // AB // CD   (1)

   + Ta tìm giao tuyến của mp(MAB) và (SCD):

Ta có: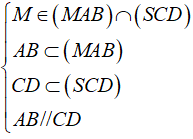

⇒ (MAB) ∩ (SCD) = d₂ ,với M ∈ d₂ và d₂ // AB // CD   (2)

   + Từ (1) và (2) suy ra: d₁ // d₂

Chọn D

Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O , I là trung điểm cạnh SC. Khẳng định nào sau đây SAI?

A. IO // SA

B. 4 điểm I, O, S và A đồng phẳng

C. giao tuyến của mp (SAB) và mp(IBD) là Bx trong đó Bx // SA // IO

D. (IBD) ∩ (SAC) = ID

Lời giải:

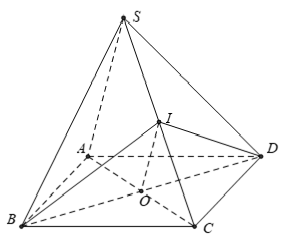
   + Xét tam giác SAC có I và O lần lượt là trung điểm của SC và AC nên OI là đường trung bình của tam giác.

⇒ SA // IO và 4 điểm S; A, I, O đồng phẳng

⇒ A và B đúng.

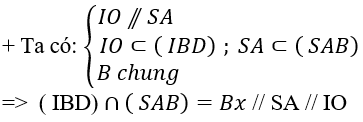
=> C đúng

nên D sai

Đáp án D

Câu 6: Cho tứ diện ABCD và M là điểm ở trên cạnh AC. Mặt phẳng (α) qua và M song song với AB và CD. Tìm giao tuyến của mp (α) và (ABD)

A. Px // MN      B. Px // AD       C. Px // AC       D. Px // BC

Lời giải:

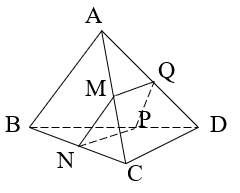
Chọn A

   + Trên mp(ABC) kẻ MN // AB, N ∈ BC

Trên mp(BCD) kẻ NP // CD, P ∈ BD

⇒ (α) chính là mặt phẳng (MNP)

   + Ta tìm giao tuyến của mp(MNP) và (ABD)

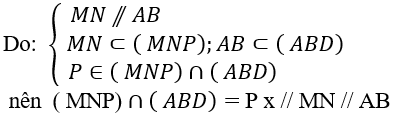
Câu 7: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm SA. Chọn mệnh đề sai

A. (IBC) ∩ (SAD) = Ix // AB // CD

B. Giao tuyến của (IBC) và (SAD) là đường trung bình của tam giác SAD.

C. A và B cùng đúng hoặc cùng sai.

D. A đúng, B sai

Lời giải:

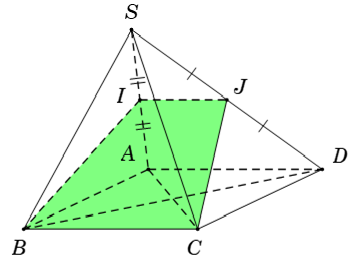
   + Ta tìm giao tuyến của mp (IBC) và (SAD) .

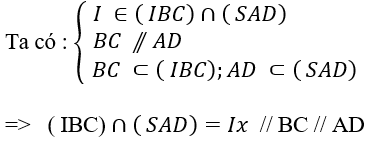
   + Trong mặt phẳng (SAD) , gọi giao điểm của Ix và SD là J.

⇒ IJ // BC

Lại có; I là trung điểm của SA nên J là trung điểm của SD.

⇒ A và B đều đúng.

Chọn D

Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M là trung điểm của SA. Gọi (P) là mặt phẳng qua điểm M và song song với SC; AD. Chọn mệnh đề sai?

A. Giao tuyến của mp(P) và mp(SAD) là đường thẳng song song với AD

B. Giao tuyến của mp(P) và mp(ABC) là đường thẳng song song với AD.

C. Giao tuyến của mp(P) và mp(SCD) là đường thẳng song song với SC.

D. Giao tuyến của mp(P) và mp(SAB) là đường thẳng song song với SC.

Lời giải:

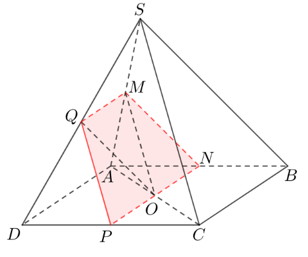
   + Qua M kẻ các đường thẳng MQ // AD và MO // SC .(với Q ∈ Sd; O ∈ AC)

Ta có: SC và AD lần lượt song song với mặt phẳng (OMQ) nên (OMQ) ≡ (P).

   + Ta có giao tuyến của (OMQ) và (SAD) là MQ và MQ //AD (theo cách dựng)

⇒ A đúng.

   + Ta tìm giao tuyến của (OMQ) và (ABCD) ta có:

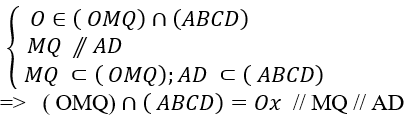
Gọi Ox cắt CD và AB lần lượt tại P và N. Khi đó; MN // AD // QM

⇒ B đúng

   + Ta tìm giao tuyến của (OMQ) và (SCD) có:

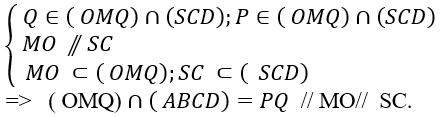
⇒ C đúng

Chọn D

Câu 9: Cho tứ diện ABCD. Gọi G và J lần lượt là trọng tâm tam giác BCD; tam giác ACD. Gọi K là trung điểm của CD. Tìm giao tuyến của hai mp(ABD) và mp(GJD)

A. Qua D và song song GJ

B. Qua A và song song AB

C. Qua D và song song GA

D. Qua J và song song AB

Lời giải:

   + Do G và J lần lượt là trọng tâm tam giác BCD; tam giác ACD nên:

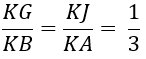
⇒ GJ // AB

   + Xét giao tuyến của hai mp(ABD) và mp(GJD):

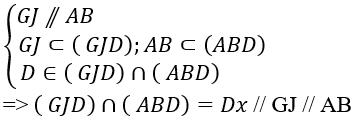
Vậy giao tuyến của mp( ABD) và mp(GJD) là đường thẳng qua D và song song AB // GJ

Chọn A