Bài tập trắc nghiệm lý thuyết về đường thẳng song song với mặt phẳng cực hay - Toán lớp 11
Bài tập trắc nghiệm lý thuyết về đường thẳng song song với mặt phẳng cực hay
Với Bài tập trắc nghiệm lý thuyết về đường thẳng song song với mặt phẳng cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập đường thẳng song song với mặt phẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Ví dụ minh họa
Ví dụ 1: Cho đường thẳng a và mặt phẳng (P) trong không gian. Có bao nhiêu vị trí tương đối của a và (P) ?
A. 2 B. 3 C. 1 D. 4
Lời giải
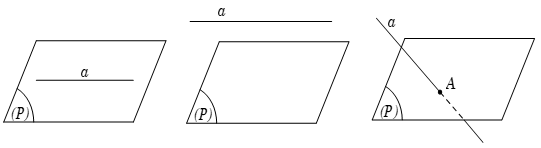
Có 3 vị trí tương đối của đường thẳng a và mp(P), đó là: a nằm trong (P), a song song với (P) và a cắt (P)
Chọn B
Ví dụ 2: Cho hai đường thẳng phân biệt a và b; mặt phẳng (α). Giả sử a // b và b // mp(α). Khi đó:
A. a // mp (α) B. a ⊂ (α) C. a cắt (α) D. a // mp(α) hoặc a ⊂ (α)
Lời giải
Chọn D
+ Trường hợp 1: Nếu a không nằm trong mp(α)
Do b // mp(α) nên tồn tại đường thẳng c ⊂ mp(α) sao cho: b // c
Lại có: a // b
Suy ra: a // c nên a // mp(α)
+ Trường hợp 2: nếu a ⊂ mp(α)
Mà a // b nên b // mp(α)
Vậy nếu a// b và b// mp(α) thì. a // mp(α) hoặc a ⊂ (α)
Ví dụ 3: Cho hai đường thẳng phân biệt a; b và mặt phẳng (α). Giả sử a // (α) và b ⊂ (α). Khi đó:
A. a // b
B. a và b chéo nhau
C. a // b hoặc a; b chéo nhau
D. a và b cắt nhau
Lời giải
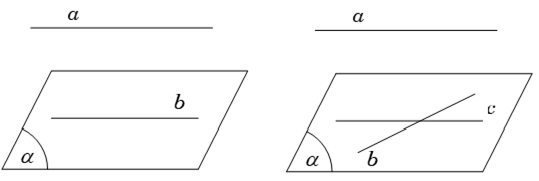
Vì a // (α) nên tồn tại đường thẳng c ⊂ (α) thỏa mãn a // c
Suy ra ; b và c đồng phẳng và xảy ra các trường hợp sau:
- Nếu b song song hoặc trùng với c thì a // b.
- Nếu b cắt c thì b cắt (β) = (a; c) nên a; b không đồng phẳng
Do đó a; b chéo nhau
Chọn C
Ví dụ 4: Cho đường thẳng a nằm trong mặt phẳng (α). Giả sử b ⊄ (α). Mệnh đề nào sau đây đúng?
A. Nếu b // (α) thì b // a
B. Nếu b cắt (α) thì b cắt a
C. Nếu b // a thì b // (α)
D. Nếu b cắt (α) và (β) chứa b thì giao tuyến của (β) và (α) là đường thẳng cắt cả a và b
Lời giải
Chọn C
- A sai. Nếu b // (α) thì b // a hoặc a; b chéo nhau
- B sai. Nếu b cắt (α) thì b cắt a hoặc a; b chéo nhau
- D sai. Nếu b cắt (α) và (β) chứa b thì giao tuyến của (α) và (β) là đường thẳng cắt a hoặc song song với a

Ví dụ 5: Cho hai đường thẳng phân biệt a; b và mặt phẳng (α). Giả sử a // (α) và b // (α). Mệnh đề nào sau đây đúng?
A. a và b không có điểm chung
B. a và b hoặc song song hoặc chéo nhau
C. a và b hoặc song song hoặc chéo nhau hoặc cắt nhau
D. a và b chéo nhau
Lời giải
Chọn C
Ví dụ 6: Cho mặt phẳng (P) và hai đường thẳng song song a và b. Khẳng định nào sau đây đúng?
A. Nếu (P) song song với a thì (P) cũng song song với b
B. Nếu (P) cắt a thì (P) cũng cắt b
C. Nếu (P) chứa a thì (P) cũng chứa b
D. Các khẳng định A, B, C đều sai.
Lời giải
Gọi mp (Q) = mp(a; b)
- A sai. Khi b = (P) ∩ (Q) ⇒ b ⊂ (P)
- C sai. Khi (P) khác (Q) thì b // (P)
- Xét khẳng định B, giả sử (P) không cắt b khi đó b ⊂ (P) hoặc b // (P)
Khi đó, vì b // a nên a ⊂ (P) hoặc a cắt (P) (mâu thuẫn với giả thiết (P) cắt a)
Vậy khẳng định B đúng
Chọn B
Ví dụ 7: Cho d // mp(α), mặt phẳng (β) qua d cắt mp(α) theo giao tuyến d’. Khi đó:
A. d // d’ B. d cắt d’ C. d và d’ cắt nhau D. d ≡ d'
Lời giải
Ta có: d’ = (α) ∩ (β)
+ Do d và d’ cùng thuộc (β) nên d cắt d’ hoặc d // d’
+ Nếu d cắt d’ . Khi đó, d cắt (α) (mâu thuẫn với giả thiết)
Vậy d // d’
Chọn A
Ví dụ 8: Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng song song với cả 2 đường thẳng.
A. 1 B. 2 C. 3 D. Vô số
Lời giải
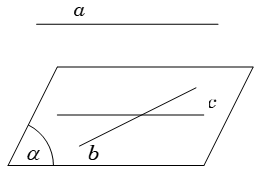
Gọi c là đường thẳng song song với a và cắt b
Gọi mp(b; c) = mp(α). Do a // c nên a // (α)
Giả sử có mp(β) // mp(α). Mà b ⊂ mp(α) nên b // mp(β)
Mặt khác, a // mp(α) nên a // mp (β)
Có vô số mặt phẳng (β) // mp(α)
Vậy có vô số mặt phẳng song song với 2 đường thẳng chéo nhau.
Chọn D.
B. Bài tập trắc nghiệm
Câu 1: Cho hai đường thẳng chéo nhau a và b. Khẳng định nào sau đây sai?
A. Có duy nhất một mặt phẳng song song với a và b
B. Có duy nhất một mặt phẳng qua a và song song với b
C. Có duy nhất một mặt phẳng qua điểm M, song song với a và b (với M là điểm cho trước).
D. Có vô số đường thẳng song song với a và cắt b.
Lời giải:
Có có vô số mặt phẳng song song với 2 đường thẳng chéo nhau.
Do đó A sai.
Chọn A
Câu 2: Cho ba đường thẳng đôi một chéo nhau a; b; c. Gọi mp (P) là mặt phẳng qua a, mp(Q) là mặt phẳng qua b sao cho giao tuyến của (P) và (Q) song song với c. Có nhiều nhất bao nhiêu mặt phẳng (P) và (Q) thỏa mãn yêu cầu trên?
A. Một mặt phẳng (P), một mặt phẳng (Q)
B. Một mặt phẳng (P), vô số mặt phẳng (Q)
C. Một mặt phẳng (Q), vô số mặt phẳng (P)
D. Vô số mặt phẳng (P) và (Q)
Lời giải:
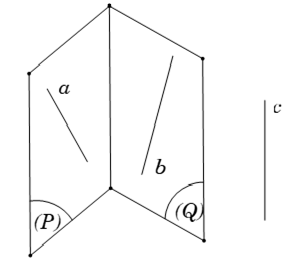
Vì c song song với giao tuyến của (P) và (Q) nên c // mp(P) và c // mp(Q)
Khi đó, (P) là mặt phẳng chứa a và song song với c; mà a và c chéo nhau nên chỉ có một mặt phẳng như vậy
Tương tự cũng chỉ có một mặt phẳng (Q) chứa b và song song với c
Vậy có nhiều nhất một mặt phẳng (P) và một mặt phẳng (Q) thỏa yêu cầu bài toán
Chọn A

Câu 3: Cho hai đường thẳng phân biệt a; b và mặt phẳng (α) . Giả sử a // mp(α); b ⊂ (α). Khi đó:
A. a // b
B. a; b chéo nhau
C. a // b hoặc a; b chéo nhau
D. a; b cắt nhau
Lời giải:
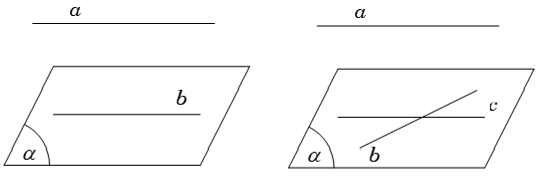
Vì a // (α) nên tồn tại đường thẳng c ⊂ (α) thỏa mãn a // c
Suy ra b, c đồng phẳng và xảy ra các trường hợp sau:
- Nếu b song song hoặc trùng với c thì a // b
- Nếu b cắt c thì b cắt (β) = (a; c) nên a; b không đồng phẳng. Do đó a; b chéo nhau.
Chọn C
Câu 4: Cho hai đường thẳng chéo nhau a và b. Khẳng định nào sau đây sai?
A. Có duy nhất một mặt phẳng song song với a và b
B. Có duy nhất một mặt phẳng qua a và song song với b
C. Có duy nhất một mặt phẳng qua điểm M , song song với a và b (với M là điểm cho trước)
D. Có vô số đường thẳng song song với a và cắt b
Lời giải:
Có có vô số mặt phẳng song song với 2 đường thẳng chéo nhau.
Do đó A sai.
Chọn A
Câu 5: Tìm mệnh đề sai
A. Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nào đó trong (P) thì a song song với (P).
B. Nếu đường thẳng a song song với mặt phẳng (P) thì mọi mặt phẳng (Q) chứa a mà cắt (P) thì sẽ cắt theo một giao tuyến song song với a
C. Nếu một đường thẳng song song với một mặt phẳng thì nó song song với một đường thẳng nào đó trong mặt phẳng.
D. Nếu a và b là hai đường thẳng chéo nhau thì qua a có vô số mặt phẳng song song với b.
Lời giải:
Chọn D
+ A; B và C đúng (là các định lí; hệ quả)
+ D sai: Nếu a và b là hai đường thẳng chéo nhau thì qua a có một và chỉ một mặt phẳng song song với b
Câu 6: Cho đường thẳng d; đường thẳng c ⊂ mp(α) và hai đường thẳng d và c chéo nhau. Tìm mệnh đề đúng về vị trí tương đối của d và mp(α)
A. Cắt nhau
B. Song song
C. cắt nhau hoặc song song
D. d ⊂ mp(α) hoặc cắt nhau
Lời giải:
+ Hai đường thẳng d và c chéo nhau
⇒ Hai đường thẳng d và c không đồng phẳng
Mà đường thẳng c ⊂ mp(α) nên đường thẳng d không thuộc mp(α)
⇒ đường thẳng d và mp(α) cắt nhau hoặc song song
⇒ C đúng
Chọn C
Câu 7: Cho hai đường thẳng a và b cắt nhau. Đường thẳng b // mp(α). Xác định vị trí tương đối của đường thẳng a và mp(α).
A. Cắt nhau
B. Song song
C. cắt nhau hoặc song song
D. d ⊂ mp(α) hoặc cắt nhau.
Lời giải:
+ Đường thẳng a và mp(α) có thể cắt nhau: Ví dụ hình chóp S.ABCD có M và N lần lượt là trung điểm của SA và SD
⇒ MN // AD (MN là đường trung bình của tam giác SAD)
Hai đường thẳng MN và SA cắt nhau tại M có MN // mp( ABCD) và SA cắt mp(ABCD) tại A
+ Đường thẳng a và mp(α) có thể song song. Ví dụ: Hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M; N; P và Q lần lượt là trung điểm của SA; SB; SC và SD. Hai đường thẳng MP và NQ cắt nhau
MP // AC nên MP // (ABCD)
NQ // BD nên NQ // (ABCD)
+ Đường thẳng a không thể nằm trong mp(α)
Vì giả sử đường thẳng a ⊂ mp(α). Gọi giao điểm của hai đường thẳng a và b là điểm M
Mà a ⊂ mp(α) nên điểm M ∈ (α)
Như vậy đường thẳng b và mp(α) có điểm chung là M nên đường thẳng b cắt mp
(α) (mâu thuẫn với b // mp(α))
Vậy đường thẳng a không thể nằm trong mp(α)
⇒ Đường thẳng a và mp(α) có thể cắt nhau hoặc song song
Chọn C
Câu 8: Cho đường thẳng a và mp(α). Đường thẳng c ⊂ mp(α). Có bao nhiêu vị trí tương đối giữa đường thẳng a và mp(α)? Biết hai đường thẳng a và c chéo nhau?
A. 2 B. 1 C. 3 D. tất cả sai
Lời giải:
+ Do hai đường thẳng a và c chéo nhau
Mà đường thẳng c ⊂ mp(α)
⇒ Đường thẳng a không nằm trong mp(α).
⇒ Đường thẳng a và mp(α) có thể song song hoặc cắt nhau.
Vậy có 2 vị trí tương đối giữa đường thẳng a và mp(α)
Chọn A

