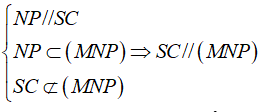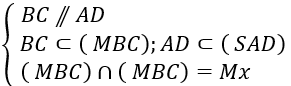Tìm thiết diện của hình chóp cắt bởi mặt phẳng chứa đường thẳng song song với đường thẳng khác - Toán lớp 11

---

Tìm thiết diện của hình chóp cắt bởi mặt phẳng chứa đường thẳng song song với đường thẳng khác

Với Tìm thiết diện của hình chóp cắt bởi mặt phẳng chứa đường thẳng song song với đường thẳng khác Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập thiết diện của hình chóp cắt bởi mặt phẳng chứa đường thẳng song song với đường thẳng khác từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

Xác định lần lượt các giao tuyến của (P) với các mặt của hình chóp theo các bước sau:

- Từ điểm chung có sẵn , xác định giao tuyến đầu tiên của (P) với một mặt của hình chóp (Có thể là mặt trung gian)

- Cho giao tuyến này cắt các cạnh của mặt đó của hình chóp ta sẽ được các điểm chung mới của (P) với các mặt khác . Từ đó xác định được các giao tuyến mới với các mặt này

- Tiếp tục như thế cho tới khi các giao tuyến khép kín ta được thiết diện .

Sử dụng định lí: Hai mặt phẳng chứa hai đường thẳng song song thì giao tuyến của chúng song song với 2 đường thẳng đó:

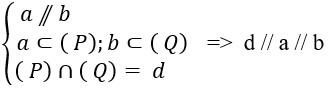
B. Ví dụ minh họa

Ví dụ 1: Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và AC; gọi E là điểm thuộc CD sao cho ED = 3EC. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD là:

A. Tam giác MNE

B. Tứ giác MNEF với F là trung điểm BD

C. Hình bình hành MNEF với F là điểm trên cạnh BD mà EF // BC

D. Hình thang MNEF với F là điểm trên cạnh BD mà EF // BC

Lời giải

   + Tam giác ABC có M; N lần lượt là trung điểm của AB; AC

Suy ra MN là đường trung bình của tam giác ABC nên MN // BC.

   + Ta tìm giao tuyến của mp (MNE) và mp(BCD) :

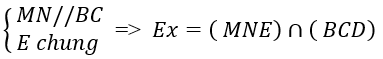
Gọi giao điểm của tia Ex và BD là F

Do đó: MN // EF suy ra bốn điểm M; N; E; F đồng phẳng và MNEF là hình thang

Vậy hình thang MNEF là thiết diện cần tìm

Chọn D

Ví dụ 2: Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng a. Các điểm M; N; P lần lượt là trung điểm của SA; SB; SC. Mặt phẳng (MNP) cắt hình chóp theo một thiết diện có diện tích bằng:

Lời giải

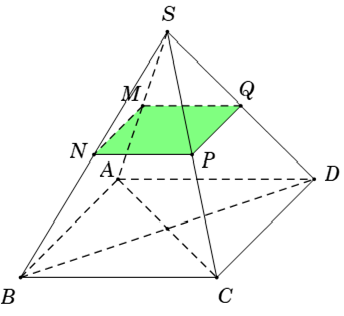
   + Do N; P lần lượt là trung điểm của SB; SC

⇒ NP là đường trung bình của tam giác SBC nên NP // BC // AD

   + Ta tìm giao tuyến của (MNP) và (SAD) có:

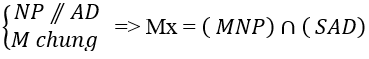
   + Trong mp ( SAD) ; gọi Mx cắt SD tại Q

⇒ Thiết diện của hình chóp là tứ giác MNPQ.

   + Tam giác SAD có M; Q lần lượt là trung điểm của SA; SD suy ra MQ // AD

   + Tam giác SBC có N; P lần lượt là trung điểm của SB; SC suy ra NP // BC

Mặt khác AD // BC suy ra MQ // NP và MQ = NP = (1/2)BC = (1/2)AD

⇒ MNPQ là hình bình hành .

   + Mà AB = AC và AB vuông góc với BC (do đây là hình chóp tứ giác đều)

⇒ MN = NP và MN vuông góc NP

⇒ MNPQ là hình vuông cạnh MN = a/2

   + Diện tích hình vuông MNPQ là S = (a/2)² = a²/4

Chọn C

Ví dụ 3: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm SA. Thiết diện của hình chóp S. ABCD cắt bởi mặt phẳng ( IBC) là:

A. Tam giác IBC

B. Hình thang IBCJ với J là trung điểm SD

C. Hình thang IGBC với G là trung điểm SB

D. Tứ giác IBCD

Lời giải

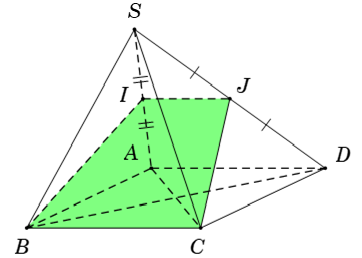
   + Ta tìm giao tuyến của mp (IBC) và (SAD)

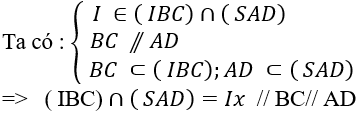
   + Trong mặt phẳng (SAD) có: Ix // AD

Gọi giao điểm của Ix và SD là J

⇒ IJ // BC

⇒ thiết diện của hình chóp S. ABCD cắt bởi mặt phẳng (IBC) là hình thang IBCJ.

Chọn B

Ví dụ 4: Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm AB và AC. Mặt phẳng (α) qua MN cắt tứ diện ABCD theo thiết diện là một đa giác. Khẳng định nào sau đây đúng?

A. Thiết diện là hình chữ nhật

B. Thiết diện là tam giác

C. Thiết diện là hình thoi

D. Thiết diện là tam giác hoặc hình thang

Lời giải

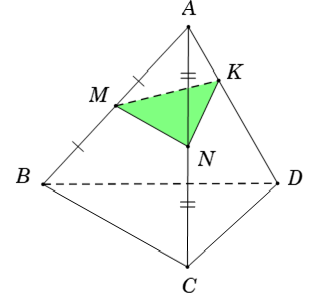
   + Trường hợp: mp (α) ∩ AD = K

⇒ Thiết diện là tam giác MNK. Do đó A và C sai.

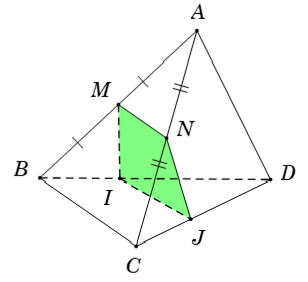
   + Trường hợp: (α) ∩ (BCD) = IJ với I ∈ BD; J ∈ CD và I; J không trùng D.

⇒ Thiết diện là tứ giác MNJI. Hơn nữa; tứ giác MNJI là hình thang

Thật vậy, do MN là đường trung bình của tam giác ABC nên MN // BC.

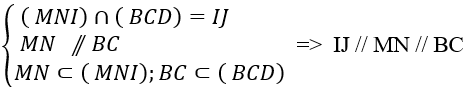
⇒ Tứ giác MNJI là hình thang

Chọn D

Ví dụ 5: Cho hai hình vuông ABCD và CDIS không thuộc một mặt phẳng và cạnh bằng 4. Biết tam giác SAC cân tại S; SB = 8. Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (ACI) có diện tích bằng:

A. 8          B. 8√2         C. 8√3         D. 10

Lời giải

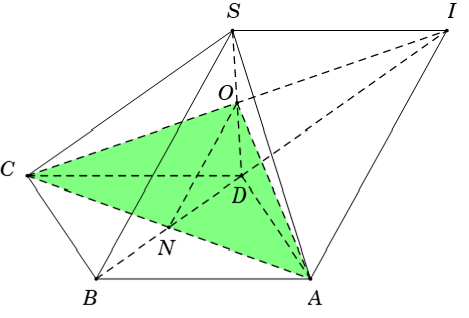
   + Gọi O là giao điềm của SD và CI; N là giao điểm của AC và BD

⇒ O; N lần lượt là trung điểm của DS và DB (do ABCD và CDSI là hình vuông)

⇒ ON là đường trung bình của tam giác SBD và ON = (1/2)SB = 4

   + Thiết diện của hình chóp S.ABCD cắt bởi mp (ACI) là tam giác OCA.

Tam giác SAC cân tại S nên SC = SA

⇒ ΔSDC = ΔSDA (c.c.c)

⇒ CO = AO (cùng là đường trung tuyến của 2 định tương ứng)

⇒ tam giác OCA cân tại O

⇒ ON là đường trung tuyến nên đồng thời là đường cao

Khi đó; diện tích tam giác OCA là:

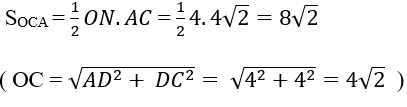
Chọn B.

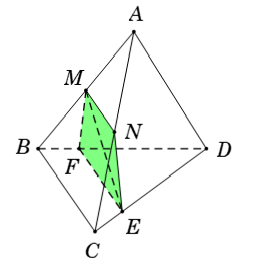
Ví dụ 6: Cho hình chóp S.ABCD có đáy hình vuông cạnh a; mặt bên SAB là tam giác đều. Cho SC = SD = a√3. Gọi H và K lần lượt là trung điểm của SA; SB. M là mộtđiềm trên cạnh AD. Thiết diện của hình chóp cắt bởi (HKM) là:

A. Tam giác

B. Tứ giác

C. Hình thanh cân

D. Hình bình hành

Lời giải

   + xét tam giác SAB có H và K lần lượt là trung điểm của SA; SB

⇒ HK là đường trung bình của tam giác SAB và HK // AB

   + xác định giao tuyến của mp(HKM) và (ABCD) có;

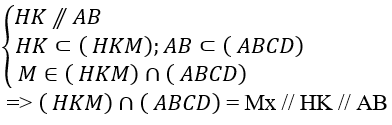
   + Trong mp ( ABCD) gọi Mx cắt BC tại N

⇒ Thiết diện của hình chóp cắt bởi mp(HKM) là hình thang KHMN

   + Xét tam giác SAD và SBC có:

⇒ Tứ giác KHMN là hình thang cân

Chọn C

Ví dụ 7: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I và J lần lượt là trọng tâm tam giác SAB và SAD. M là trung điểm của CD. Xác định thiết diện của hình chóp với mp(IJM)

A. Tứ giác          B. Ngũ giác         C. Hình thang         D. Hình thang cân

Lời giải

   + Gọi H và K lần lượt là trung điểm của AD; AB

   + Do I và J là trọng tâm tam giác SAB và SAD nên: SJ/SH = SI/SK = 2/3

⇒ IJ // HK

   + Xác định giao tuyến của (IJM) và (ABCD):

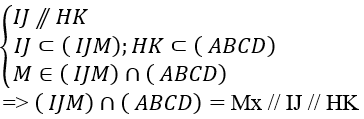
   + Trong mp (ABCD); Mx cắt BC tại N

⇒ Thiết diện của hình chóp với mp(IJM) là tứ giác IJMN

   + Lại có: IJ // MN

⇒ Tứ giác IJMN là hình thang

Chọn C

Ví dụ 8: Cho hình chóp S.ABCD đáy là hình thang, đáy lớn AB. Gọi M là điểm trên cạnh SB sao cho SM/SB = 1/4. Gọi H; K lần lượt là trung điểm của AD và BC. Tìm mối liên hệ giữa AB và CD để thiết diện của hình chóp cắt bởi (HKM) là hình bình hành?

A. AB = 2CD

B. AB = 3CD

C. AB = 4CD

D. Thiết diện không thể là hình bình hành

Lời giải

   + Xét hình thang ABCD có H và K lần lượt là trung điểm của AD và BC.

⇒ HK là đường trung bình của hình thang.

⇒ HK // AB // CD.

   + Xác định giao tuyến của mp(HKM) và (SAB):

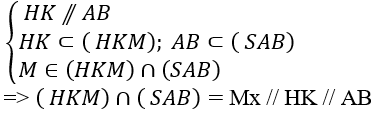
   + Trong mp(SAB); Mx cắt SA tại N

⇒ Thiết diện là tứ giác HKMN.

   + Để thiết diện là hình bình hành khi : MN = HK.

   + Lại có: HK = (AB + CD)/2 ( tính chất đường trung bình của hình thang )    (1)

   + Do MN // AB nên áp dụng hệ quả định lí Ta-let:

SM/SB = MN/AB = 1/4. ⇔ MN = (AB)/4   (2)

Từ ( 1) và (2) suy ra: (AB + CD)/2 = (AB)/4

⇔ 4( AB + CD) = 2AB ⇔ 2AB + 4CD = 0

Vô lí vì AB > 0 và CD > 0

⇒ Thiết diện của hình chóp cắt bởi (HKM) không thể là hình bình hành.

Chọn D

C. Bài tập trắc nghiệm

Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M là trung điểm của SA. Thiết diện của mặt phẳng (P) với hình chóp S.ABCD là hình gì? biết (P) là mặt phẳng qua điểm M và song song với SC; AD.

A. Tam giác         B. Tam giác cân          C. tứ giác         D. Hình thang

Lời giải:

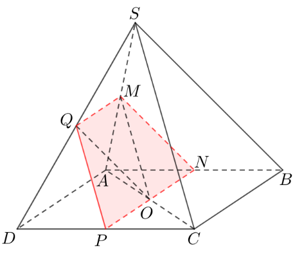
   + Qua M kẻ các đường thẳng MQ // AD và MO // SC

Ta có: SC và AD lần lượt song song với mặt phẳng (OMQ) nên (OMQ) ≡ (P)

   + Dễ dàng tìm được: (OMQ) ∩ (ABCD) = NP, với NP // MQ // BC và O ∈ NP. Từ đó ta có:

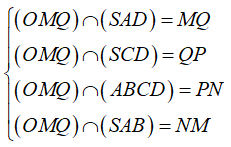
vậy thiết diện tạo bởi (P) và hình chóp là hình thang MNPQ

Câu 2: Cho hình chóp S.ABCD. Gọi M; N là hai điểm trên SB; CD và (P) là mặt phẳng qua MN và song song với SC. Thiết diện của hình chóp và mặt phẳng (P) là?

A. Tam giác cân      B. Tứ giác       C. Hình thang         D. Tam giác hoặc tứ giác

Lời giải:

Chọn C

   + Ta xác định mp ( P) và tìm giao tuyến của mp(P) với các mặt của hình chóp.

- Qua N kẻ NP // SC

Ta có:

Từ đó ta có: (MNP) là mặt phẳng qua MN và song song với SC

Vậy P ≡ (MNP)

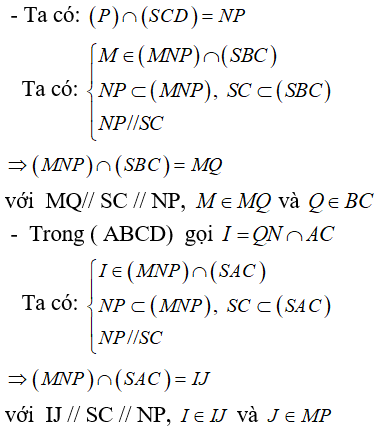
⇒ Thiết diện tạo bởi (P) và hình chóp là tứ giác MPNQ

- theo cách dựng ta có; MP // NQ (cùng // SC)

⇒ MPNQ là hình thang.

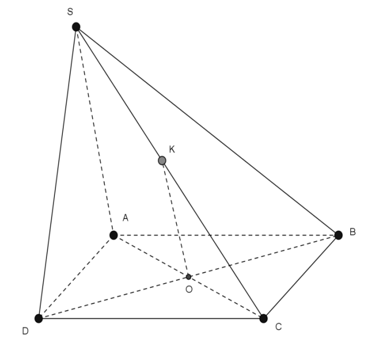
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng (α) qua BD và song song với SA, mặt phẳng (α) cắt SC tại K. Khẳng định nào sau đây là khẳng định đúng ?

A. SK = 2KC

B. SK = KC

C. Thiết diện của hình chóp cắt bởi mp(α) là tứ giác

D. Tất cả sai

Lời giải:

Chọn B

   + Gọi O là giao điểm của AC và BD. Do mặt phẳng (α) qua BD nên O ∈ (α)

   + Trong tam giác SAC, kẻ OK song song SA (K ∈ SC)

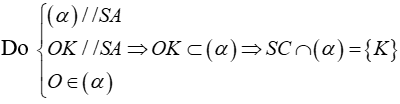
   + Trong tam giác SAC ta có

là đường trung bình của ΔSAC

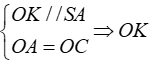
Vậy SK = KC

   + Mp(α) ≡ mp(KBD) nên thiết diện của hình chóp cắt bởi mp(KBD) là tam giác KBD.

Câu 4: Cho hình chóp S. ABCD có đáy ABCD là hình thang, AD // BC và AD = 2 BC, M là trung điểm SA. Mặt phẳng (MBC) cắt hình chóp theo thiết diện là

A. tam giác    B. hình bình hành.     C. hình thang vuông.     D. hình chữ nhật.

Lời giải:

Chọn B

   + Ta có:

⇒ Mx // BC // AD; gọi Mx cắt SD tại N

⇒ Thiết diện của hình chóp cắt bởi mp( MBC) là tứ giác MNCB

   + Ta có: MN // AD // BC nên MNCB là hình thang

Lại có MN // AD và M là trung điểm SA

⇒ MN là đường trung bình của tam giác SAD và MN = (1/2)AD = BC

⇒ thiết diện MNCB là hình bình hành.

Câu 5: Cho tứ diện ABCD và M là điểm ở trên cạnh AC. Mặt phẳng (α) qua và M song song với AB và CD. Thiết diện của tứ diện cắt bởi (α) là

A. hình bình hành    B. hình chữ nhật    C. hình thang    D. hình thoi.

Lời giải:

Chọn A

   + Trên mp(ABC) kẻ MN // AB; N ∈ BC

Trên mp(BCD) kẻ NP // CD; P ∈ BD

⇒ (α) chính là mặt phẳng (MNP)

Gọi giao điểm của Px và AD là Q. Vậy MN // PQ // AB   (1)

Khi đó, thiết diện của hình chóp cắt bởi mp( MNP) là tứ giác MNPQ.

   + Ta có; 3 mp(MNP); mp(ACD) và mp(BCD) đôi một cắt nhau theo 3 giao tuyến là MQ; NP và CD

⇒ MQ // NP // CD (định lí giao tuyến 3 mặt phẳng)   (2)

Từ (1) và (2) suy ra thiết diện MNPQ là hình bình hành

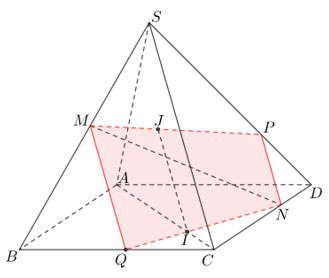
Câu 6: Cho hình chóp S. ABCD có đáy ABCD là hình thang với các cạnh đáy là AB và CD. Gọi I; J lần lượt là trung điểm của các cạnh AD và BC và G là trọng tâm của tam giác SAB.

Tìm điều kiện của AB và CD để thiết diện của (IJG) và hình chóp là một hình bình hành.

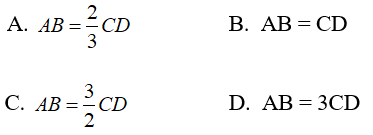
Lời giải:

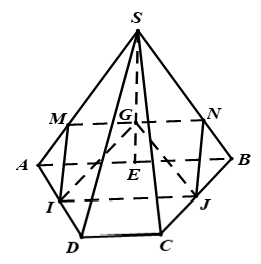
   + Tìm thiết diện của hình chóp cắt bởi mp(IJG):

Ta có ABCD là hình thang và I; J là trung điểm của AD; BC

⇒ IJ là đường trung bình của hình thang ABCD và IJ // AB.

Giao tuyến của mp (IJG) và mp (SAB):

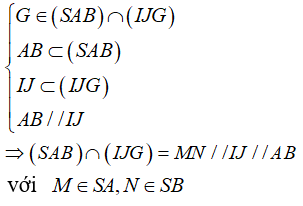
   + Dễ thấy thiết diện là tứ giác MNIJ

Do G là trọng tâm tam giác SAB và MN // AB nên theo hệ quả định lí Ta-let ta có: MN/AB = SG/SE = 2/3 (với E là trung điểm của AB)

⇒ MN = (2/3)AB

   + Lại có IJ là đường trung bình của hình thang ABCD nên IJ = (1/2)(AB + CD)

Vì MN // IJ nên MNIJ là hình thang

Do đó MNIJ là hình bình hành khi MN = IJ

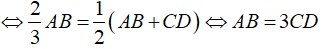
Vậy thết diện là hình bình hành khi AB = 3CD

Chọn D

Câu 7: Cho tứ diện ABCD các cạnh bằng nhau. Gọi I và J lần lượt là trung điểm của AC và BC. Gọi K là một điểm trên cạnh BD với KB = 2KD. Hỏi thiết diện của tứ diện với mp(IJK) là hình gì?

A. Tam giác

B. Tứ giác

C. Hình thang

D. Hình thang cân

Lời giải:

   + Xét tam giác ABC có I và J lần lượt là trung điểm của AC và BC nên

IJ là đường trung bình của tam giác ABC

⇒ IJ // AB

   + Ta tìm giao tuyến của mp(IJK) và (ABD):

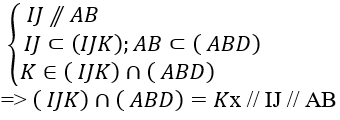
   + Trong mp(ABD); kẻ Kx // IJ // AB và Kx cắt AD tại H

⇒ Thiết diện của hình chóp cắt bởi mp( IJK) là hình thang IJKH.

   + Lại có; tứ diện ABCD có các cạnh bằng nhau nên :

ΔACD = ΔBCD (c.c.c)

⇒ IH = JK

Vậy thiết diện IJKH là hình thang cân

Chọn D