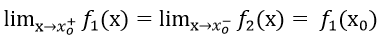Các dạng bài tập Hàm số liên tục chọn lọc, có lời giải - Toán lớp 11

---

Các dạng bài tập Hàm số liên tục chọn lọc, có lời giải

Với Các dạng bài tập Hàm số liên tục chọn lọc, có lời giải Toán lớp 11 tổng hợp các dạng bài tập, 100 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Hàm số liên tục từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

• Dạng 1: Xét tính liên tục của hàm số Xem chi tiết
• Dạng 2: Tìm m để hàm số liên tục Xem chi tiết
• 40 bài tập trắc nghiệm Hàm số liên tục có đáp án Xem chi tiết

Cách xét tính liên tục của hàm số

A. Phương pháp giải & Ví dụ

Vấn đề 1: Xét tính liên tục của hàm số tại một điểm

- Cho hàm số y = f(x) có tập xác định D và điểm x₀ ∈ D. Để xét tính liên tục của hàm số trên tại điểm x = x₀ ta làm như sau:

       + Tìm giới hạn của hàm số y = f(x) khi x → x₀ và tính f(x₀)

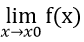
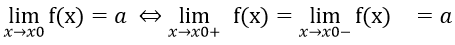
       + Nếu tồn tại thì ta so sánh

với f(x₀).

Nếu 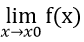=     f(x₀) thì hàm số liên tục tại x₀

Chú ý:

1. Nếu hàm số liên tục tại x₀ thì trước hết hàm số phải xác định tại điểm đó.

2.

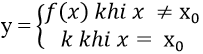
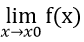
3. Hàm số liên tục tại x = x₀ ⇔ = k

4. Hàm số 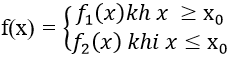liên tục tại điểm x = x₀ khi và chỉ khi

Vấn đề 2: Xét tính liên tục của hàm số trên một tập

Ta sử dụng các định lí về tính liên tục của hàm đa thức, lương giác, phân thức hữu tỉ …

Nếu hàm số cho dưới dạng nhiều công thức thì ta xét tính liên tục trên mỗi khoảng đã chia và tại các điểm chia của các khoảng đó.

Ví dụ minh họa

Bài 1: Xét tính liên tục của hàm số sau tại x = 3

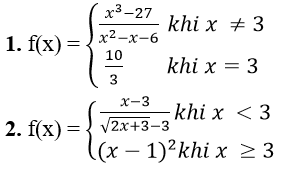
Hướng dẫn:

1. Hàm số xác định trên R

Ta có f(3) = 10/3 và

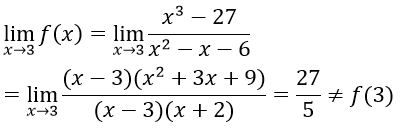
Vậy hàm số không liên tục tại x = 3

2. Ta có f(3) = 4 và

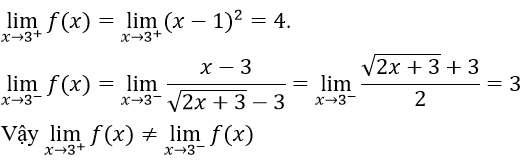
Vậy hàm số gián đoạn tại x = 3

Bài 2: Xét tính liên tục của các hàm số sau trên toàn trục số

1. f(x) = tan2x + cosx

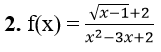
Hướng dẫn:

1. TXĐ: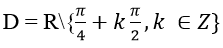

Vậy hàm số liên tục trên D

2. Điều kiện xác định:

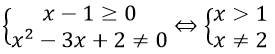
Vậy hàm số liên tục trên (1;2) ∪ (2,+∞)

Bài 3: Xét tính liên tục của hàm số sau tại điểm chỉ ra

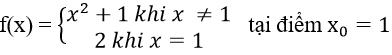
Hướng dẫn:

Ta có

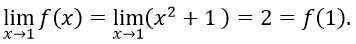
Vậy hàm số liên tục tại x = 1

Cách tìm m để hàm số liên tục

A. Phương pháp giải & Ví dụ

Ta sử dụng điều kiện để hàm số liên tục và điều kiện để phương trình có nghiệm để làm các bài toán dạng này.

- Điệu kiện để hàm số liên tục tại x₀:

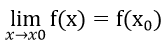
- Điều kiện để hàm số liên tục trên một tập D là f(x) liên tục tại mọi điểm thuộc D.

- Phương trình f(x) = 0 có ít nhất một nghiệm trên D nếu hàm số y = f(x) liên tục trên D và có hai số a, b thuộc D sao cho f(a).f(b) < 0.

Phương trình f(x) = 0 có k nghiệm trên D nếu hàm số y = f(x) liên tục trên D và tồn tại k khoảng rời nhau (a_i ; a_i+1) (i = 1,2,…,k) nằm trong D sao cho f(a_i).f(a_i+1) < 0.

Ví dụ minh họa

Bài 1: Xác định a để hàm số 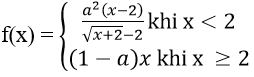liên tục trên R.

Hướng dẫn:

Hàm số xác định trên R

Với x < 2 ⇒ hàm số liên tục

Với x > 2 ⇒ hàm số liên tục

Với x = 2 ta có

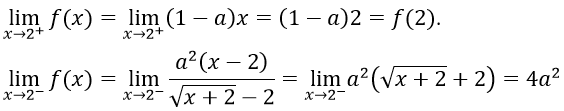
Hàm số liên tục trên R ⇔ hàm số liên tục tại x = 2

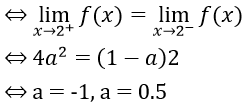
Vậy a = -1, a = 0.5 là những giá trị cần tìm.

Bài 2: Cho hàm số f(x) = x³ – 1000x² + 0,01 . phương trình f(x) = 0 có nghiệm thuộc khoảng nào trong các khoảng sau đây ?

I. (–1; 0)            II. (0; 1)            III. (1; 2)

Hướng dẫn:

Ta có hàm số y = f(x) = x³ – 1000x² + 0,01 là hàm liên tục trên R

f(0) = 0.01 và f(-1) = - 1001 + 0.01 < 0. Nên f(0).(-1) < 0.

Vậy hàm số có nghiệm trong khoảng I

Bài 3: Tìm m để các hàm số sau liên tục trên R

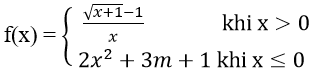
Hướng dẫn:

Với x < 0 ⇒ hàm số liên tục

Với x > 0 ⇒ hàm số liên tục

Với x = 0 ta có

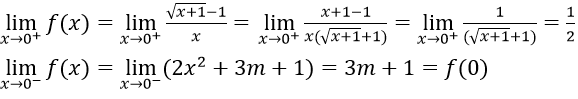
Hàm số liên tục trên R ⇔ hàm số liên tục tại x = 0