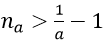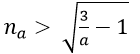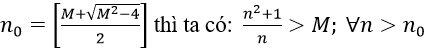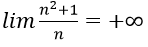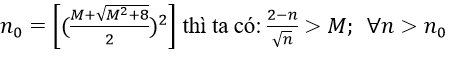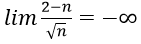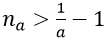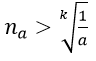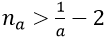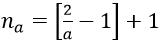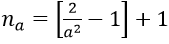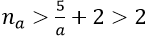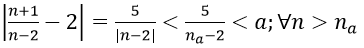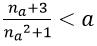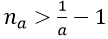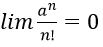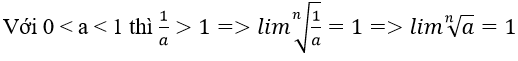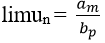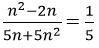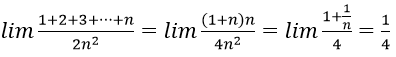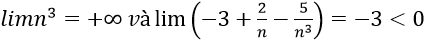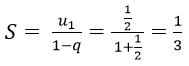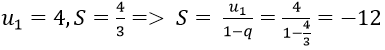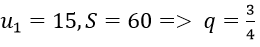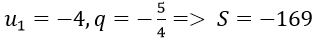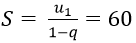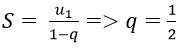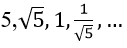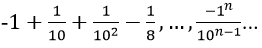Các dạng bài tập Giới hạn của dãy số chọn lọc, có lời giải - Toán lớp 11

---

Các dạng bài tập Giới hạn của dãy số chọn lọc, có lời giải

Với Các dạng bài tập Giới hạn của dãy số chọn lọc, có lời giải Toán lớp 11 tổng hợp các dạng bài tập, 100 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Giới hạn của dãy số từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

• Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa Xem chi tiết
• Dạng 2: Tổng của cấp số nhân lùi vô hạn Xem chi tiết
• Dạng 3: Tính giới hạn của dãy số Xem chi tiết
• Cách tính giới hạn của dãy số có chứa căn thức cực hay, chi tiết Xem chi tiết
• 60 bài tập trắc nghiệm Giới hạn của dãy số có đáp án Xem chi tiết

Cách tìm giới hạn của dãy số bằng định nghĩa

A. Phương pháp giải & Ví dụ

- Để chứng minh limu_n = 0 ta chứng minh với mọi số a > 0 nhỏ tùy ý luôn tồn tại một số n_a sao cho |u_n|<a ∀n > n_a.

- Để chứng minh limu_n = 1 ta chứng minh lim(u_n-1) = 0.

- Để chứng minh limu_n = +∞ ta chứng minh với mọi số M > 0 lớn tùy ý, luôn tồn tại số tự nhiên n_M sao cho u_n > M ∀n > n_M.

- Để chứng minh limu_n = -∞ ta chứng minh lim(-u_n) = +∞

- Một dãy số nếu có giới hạn thì giới hạn đó là duy nhất.

Ví dụ minh họa

Bài 1: Chứng minh rằng:

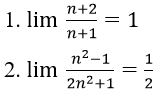
Hướng dẫn:

1. Với a > 0 nhỏ tùy ý, ta chọn

Ta có:

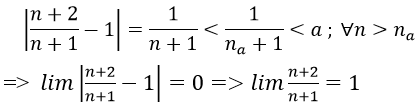
2. Với a > 0 nhỏ tùy ý, ta chọn

Ta có:

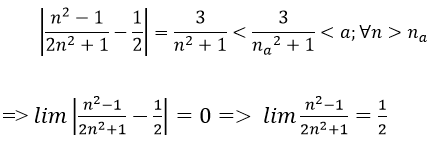
Bài 2: Chứng minh rằng dãy số (u_n ) : u_n = (-1)ⁿ không có giới hạn.

Hướng dẫn:

Ta có: u_2n = 1 ⇒ limu_2n = 1; u_(2n+1) = -1 ⇒ limu_(2n+1) = -1

Vì giới hạn của dãy số nếu có là duy nhất nên ta suy ra dãy (u_n) không có giới hạn.

Bài 3: Chứng minh các giới hạn sau:

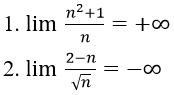
Hướng dẫn:

1. Với mọi số thực dương M lớn tùy ý, ta có:

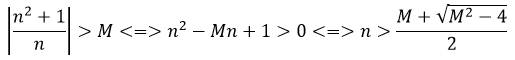
Ta chọn

Do đó:

2. Với mọi M > 0 lớn tùy ý, ta có:

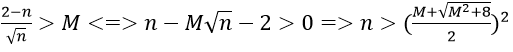
Ta chọn

Do đó:

Bài 4: Chứng minh rằng:

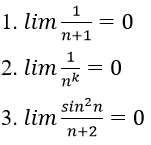
Hướng dẫn:

1. Với a > 0 nhỏ tùy ý, ta chọn

Ta có:

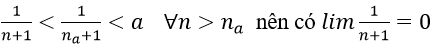
2. Với a > 0 nhỏ tùy ý, ta chọn

Ta có:

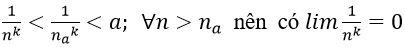
3. Với a > 0 nhỏ tùy ý, ta chọn

Ta có:

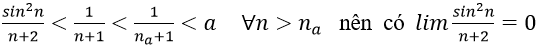
Bài 5: Chứng minh các giới hạn sau

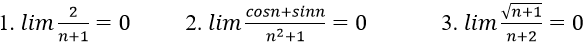
Hướng dẫn:

1. Với mọi a > 0 nhỏ tùy ý, ta chọn

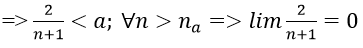
2. Ta có

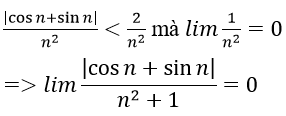
3. Với mọi số thực a > 0 nhỏ tùy ý, ta chọn

Ta có:

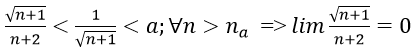
Bài 6: Dùng định nghĩa tìm các giới hạn sau :

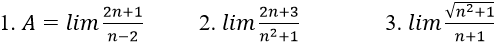
Hướng dẫn:

1. Với số thực a > 0 nhỏ tùy ý, ta chọn

Ta có:

Vậy A = 2

2. Với số thực a > 0 nhỏ tùy ý, ta chọn n_a thỏa mãn

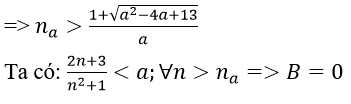
3. Với số thực a > 0 nhỏ tùy ý, ta chọn

Ta có:

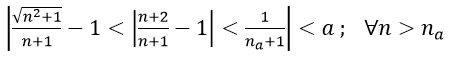
Vậy C = 1

Bài 7: Chứng minh rằng dãy số (u_n): u_n = (-1)ⁿ không có giới hạn.

Hướng dẫn:

Ta có: u_2n → +∞; u_(2n+1) = -(2n+1) → -∞

Do đó dãy số đã cho không có giới hạn.

Bài 8: Chứng minh các giới hạn sau:

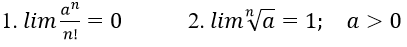
Hướng dẫn:

1. Gọi m là số tự nhiên thỏa: m+1 > |a|. Khi đó với mọi n > m+1

Ta có:

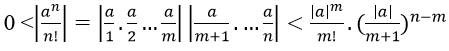
Mà 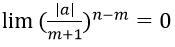Từ đó suy ra:

2. Nếu a = 1 thì ta có đpcm

+ Giả sử a > 1. Khi đó:

+

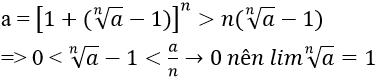
Tóm lại ta luôn có: 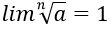với a > 0.

B. Bài tập vận dụng

Bài 1: Dãy số nào sau đây có giới hạn khác 0 ?

Lời giải:

Đáp án: C

Cách 1.

= lim⁡1 + lim(1/n) = 1 + 0 = 1

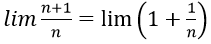
Đáp án C

Cách 2 (phương pháp loại trừ). Từ các định lí ta thấy:

Các dãy ở phương án A,B đều bằng 0, do đó loại phương án A,B

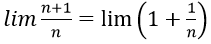
Do đó loại phương án D

Chọn đáp án C

Bài 2: Dãy số nào sau đây có giới hạn bằng 0 ?

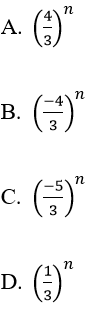
Lời giải:

Đáp án: D

Cách 1. Dãy (1/3)ⁿ có giới hạn 0 vì |q| < 1 thì limqⁿ = 0. Đáp án là D

Cách 2. Các dãy ở các phương án A,B,C đều có dạng limqn nhưng |q| > 1 nên không có giưới hạn 0, do đó loại phương án A,B,C. Chọn đáp án D

Bài 3: 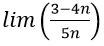có giá trị bằng:

Lời giải:

Đáp án: D

Cách 1. Chia tử và mẫu xủa phân tử cho n (n là luỹ thừa bậc cao nhất của n trong tử và mẫu của phân thức), ta được

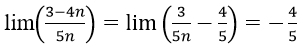
Đáp án là D

Cách 2. Sử dụng nhận xét:

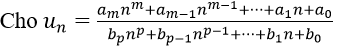
khi tính limu_n ta thường chia tử và mẫu của phân thức cho n^k (n^k là luỹ thừa bậc cao nhất của n trong tử và mẫu của phân thức), từ đó được kết quả:

Nếu m < p thì limu_n = 0. Nếu m = p thì

Nếu m > p thì limu_n = +∞ nếu a_m.b_p > 0; limu_n = -∞ nếu a_m.b_p < 0

Vì tử và mẫu của phân thức đã cho đều có bậc 1 nên kết quả

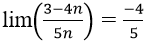
Do đó chọn đáp án là D

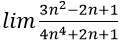
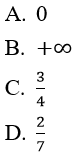
Bài 4: bằng:

Lời giải:

Đáp án: A

Cách 1. Sử dụng nhận xét trên, vì bậc của tử thức nhỏ hơn bậc của mẫu thức nên kết quả

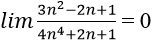
Đáp án là A

Cách 2. Chia tử và mẫu của phân thức cho n⁴(n⁴ là luỹ thừa bậc cao nhất của n trong tử và mẫu của phân thức) rồi tính. Đáp án A

Bài 5: 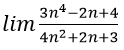bằng:

Lời giải:

Đáp án: B

Cách 1. Sử dụng nhận xét trên, vì bậc của tử thức lớn hơn bậc của mẫu thức, hệ số luỹ thừa bậc cao nhất của n cả tử và mẫu là số dương nên kết quả

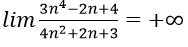
Đáp án là B

Cách 2. Chia tử và mẫu của phân thức cho n⁴(n⁴ là luỹ thừa bậc cao nhất của n trong tử và mẫu của phân thức) rồi tính. Đáp án B

Bài 6: Dãy số nào sau đây có giưới hạn bằng 1/5 ?

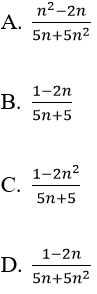
Lời giải:

Đáp án: A

Cách 1. Tính được

Suy ra đáp án là A

Cách 2. . Sử dụng nhận xét trên, vì bậc của tử thức lớn hơn bậc của mẫu thức, hệ số luỹ thừa bậc cao nhất của n cả tử và mẫu thức bằng nhau và tỉ số hệ số của cúng bằng 1/5. Chỉ có dãy ở phương án A thoả mãn. Vậy đáp án là A.

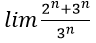
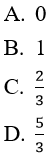
Bài 7: có giá trị bằng:

Lời giải:

Đáp án: B

Ta có:

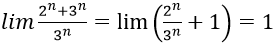
Đáp án B

Bài 8: 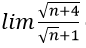có giá trị bằng:

Lời giải:

Đáp án: A

chia cả tử thức và mẫu thức cho √n

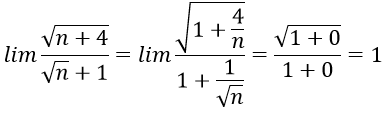
Đáp án A

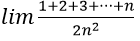
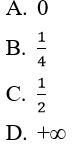
Bài 9: bằng:

Lời giải:

Đáp án: B

Trước hết tính

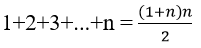
Do đó

Đáp án là B

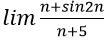
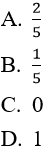
Bài 10: bằng:

Lời giải:

Đáp án: D

Chia cả tử thức mẫu thức cho n, ta có:

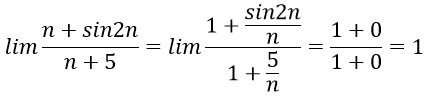
Đáp án D

Bài 11: lim⁡(-3n³ + 2n² - 5) bằng:

A. -3         B.0         C. -∞          D. +∞

Lời giải:

Đáp án: C

Ta có:

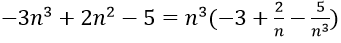
Vì

nên lim⁡(-3n³ + 2n² - 5) = -∞

Đáp án C

Bài 12: Lim( 2n⁴ + 5n² - 7n ) bằng:

A. -∞         B.0         C. 2          D. +∞

Lời giải:

Đáp án: D

Ta có:

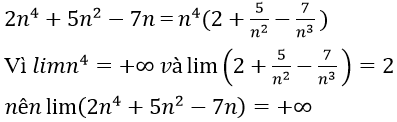
Đáp án D

Bài 13: Dãy số nào sau đây có giưới hạn là +∞ ?

A. u_n = 9n² - 2n⁵

B. u_n = n⁴ - 4n⁵

C. u_n = 4n² - 3n

D. u_n = n³ - 5n⁴

Lời giải:

Đáp án: C

Chỉ có dãy u_n = 4n² - 3n có giới hạn là +∞, các dãy còn lại đều có giới hạn là -∞.

Đáp án C

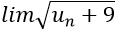
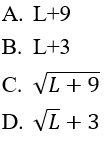
Bài 14: Nếu limu_n = L, u_n + 9 > 0 ∀n thì bằng số nào sau đây?

Lời giải:

Đáp án: C

vì limu_n = L nên lim⁡(u_n + 9) = L + 9 do đó

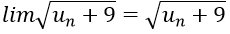
Đáp án là C

Bài 15: 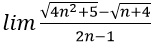bằng:

A. 0         B.1         C. 2          D. +∞

Lời giải:

Đáp án: B

Cách 1. Chia tử thức và mẫu thức cho n:

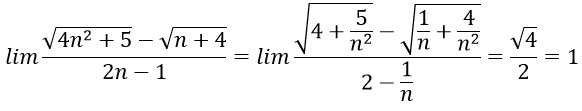
Đáp án là B

Cách 2. Thực chất có thể coi bậc cao nhất của tử thức và mẫu thức là 1, do đó chỉ cần để ý hệ số bậc 1 của tử thức là √4, của mẫu thức là 2, từ đó tính được kết quả bằng 1. Đáp án B

Cách tính tổng của cấp số nhân lùi vô hạn

A. Phương pháp giải & Ví dụ

Tổng của CSN lùi vô hạn

Cấp số nhân vô hạn u₁, u₂, u₃,..u_n,..có công bội q, với |q| < 1 gọi là cấp số nhân lùi vô hạn.

Tổng S của cấp số nhân đó là:

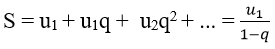
Ví dụ minh họa

Bài 1: Tìm tổng của cấp số nhân vô hạn sau:

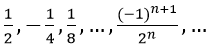
Hướng dẫn:

Đây là tổng của cấp số nhân vô hạn có

nên tổng là

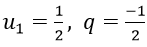
Bài 2: Tìm tổng của cấp số nhân lùi vô hạn (u_n) biết u_n = 1/(3ⁿ)

Hướng dẫn:

Vì

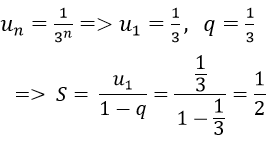
Bài 3: Tìm tổng của cấp số nhân vô hạn:

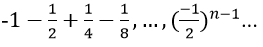
Hướng dẫn:

Vì các số của tổng lập thành cấp số nhân lùi vô hạn với u₁ = 1, q = -1/2

Vậy

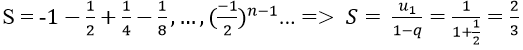
Bài 4: Tìm số hạng tổng quát của cấp số nhân lùi vô hạn có tổng bằng 3 và công bội q = 2/3

Hướng dẫn:

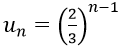
Bài 5: Tìm tổng của dãy số sau:

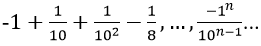
Hướng dẫn:

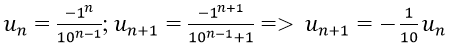
Vì vậy các số của tổng lập thành cấp số nhân lùi vô hạn với u₁ = -1, q = -1/10

Vậy

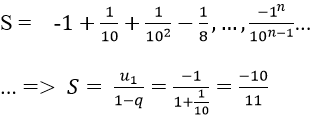
Bài 6: Tổng của một cấp số nhân lùi vô hạn là 5/3 tổng ba số hạng đầu tiên của nó là 39/25. Tìm số hạng đầu và công bội của cấp số đó.

Hướng dẫn:

Ta có

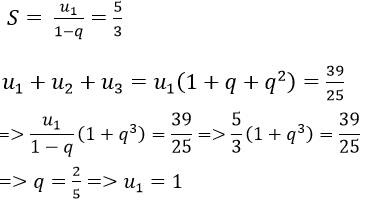
Bài 7: Cho dãy số (u_n) với 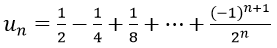. Tính tổng của dãy u_n

Hướng dẫn:

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 1/2 và q = (-1)/2.

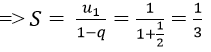
B. Bài tập vận dụng

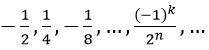
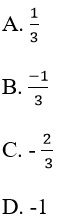
Bài 1: Tổng của cấp số nhân vô hạn: là:

Lời giải:

Đáp án: B

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = (-1)/2 và q = (-1)/2.

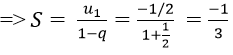
Chọn đáp án B

Bài 2: Tổng của cấp số nhân vô hạn: 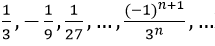là:

Lời giải:

Đáp án: A

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 1/3 và q = (-1)/3.

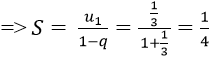
Chọn đáp án A

Bài 3: Tổng của cấp số nhân vô hạn 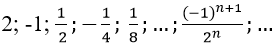là:

Lời giải:

Đáp án: A

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 2 và q = (-1)/2.

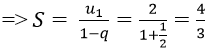
Chọn đáp án A

Bài 4: Tổng của cấp số nhân vô hạn 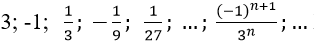là:

Lời giải:

Đáp án: C

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 3 và q = (-1)/3.

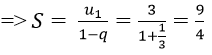
Chọn đáp án C

Bài 5: Tổng của cấp số nhân vô hạn: 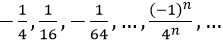là:

Lời giải:

Đáp án: A

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = (-1)/4 và q = (-1)/4.

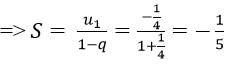
Chọn đáp án A

Bài 6: Kết quả nào sau đây là đúng:

A. Cấp số nhân lùi vô hạn (u_n) có công bội q thì tổng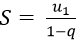

B. Cấp số nhân lùi vô hạn (u_n) có

C. Cấp số nhân lùi vô hạn (u_n) có

D. Cấp số nhân lùi vô hạn (u_n) có

Lời giải:

Đáp án: C

Vì q = (3/4) < 1 đây là cấp số nhân lùi vô hạn nên

Chọn C

Bài 7: Cấp số nhân lùi vô hạn (u_n) có u₁ = -50, S = 100. Tìm 5 số hạng đầu tiên của dãy:

A. 50; 25; 12,5; 6,5; 3,25

B. 50; 25,5; 12,5; 6,25; 3,125

C. 50; 25; 12,5; 6,25; 3,125

D. 50; 25; 12,25; 6,125; 3,0625

Lời giải:

Đáp án: C

Áp dụng công thức :

Suy ra 5 số hạng đầu tiên của dãy số: 50; 25; 12,5; 6,25; 3,125

Chọn C

Bài 8: Cấp số nhân lùi vô hạn (u_n) có u₁ = -1, q = x. Tìm tổng S và 3 số hạng đầu của cấp số này:

A.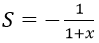 và -1, x, -x²

B.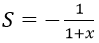 và -1, x, x²

C.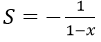 và -1, -x, -x²

D.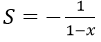 và -1, x, -x²

Lời giải:

Đáp án: C

số hạng đầu là -1, -x, -x²

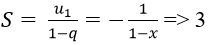
Chọn C

Bài 9: Cấp số nhân lùi vô hạn (u_n) có u₁ = -x, q = x². Tìm tổng S và 3 số hạng đầu của cấp số này:

A.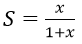 và -x, x³, x⁵

B.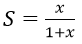 và -x, x³, x⁴

C.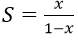 và -x, x³, x⁶

D.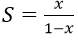 và -x, -x³, -x⁶

Lời giải:

Đáp án: D

số hạng đầu là - x, -x³, -x⁶

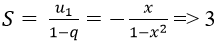
Chọn D

Bài 10: Tìm tổng của cấp số nhân vô hạn sau:

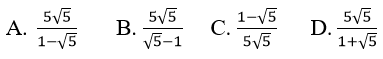
Lời giải:

Đáp án: D

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 5 và q = 1/√5.

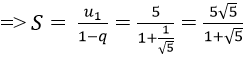
Chọn đáp án D

Bài 11: Tìm tổng của cấp số nhân vô hạn sau: -3; 0,3; -0,03; 0,003;...

Lời giải:

Đáp án: A

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = -3 và q = 0,1

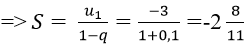
Chọn đáp án A

Bài 12: Tìm tổng

A. 4 + 2√2

B. 4 - 2√2

C. -4 + 2√2

D. -4 + 2√2

Lời giải:

Đáp án: B

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 2 và q = 1/√2

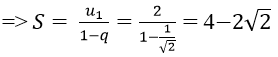
Chọn đáp án B

Bài 13: Cho cấp số nhân lùi vô hạn sau: 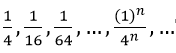Tìm q

Lời giải:

Đáp án: A

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân nên q = (1/4)

Chọn đáp án A

Bài 14: Tìm tổng của dãy số sau:

Lời giải:

Đáp án: D

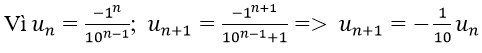
Vì vậy các số của tổng lập thành cấp số nhân lùi vô hạn với u₁ = -1, q = (-1)/10

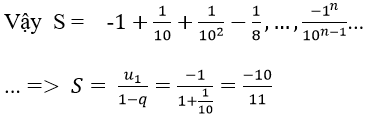
Chọn đáp án D

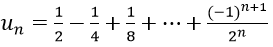
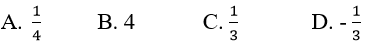
Bài 15: Cho dãy số (u_n) với . Tính tổng của dãy u_n

Lời giải:

Đáp án: C

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 1/2 và q = (-1)/2.

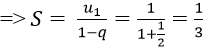
Chọn đáp án C