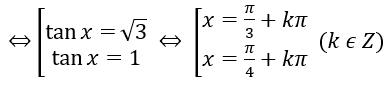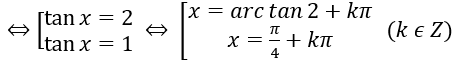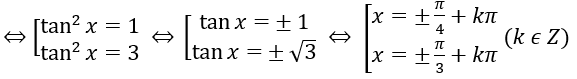Cách giải phương trình đẳng cấp bậc 2, bậc 3 lượng giác cực hay - Toán lớp 11

---

Cách giải phương trình đẳng cấp bậc 2, bậc 3 lượng giác cực hay

Với Cách giải phương trình đẳng cấp bậc 2, bậc 3 lượng giác cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập phương trình đẳng cấp bậc 2, bậc 3 lượng giác từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải & Ví dụ

Định nghĩa: Phương trình đẳng cấp đối với sinx và cosx là phương trình có dạng f(sinx, cosx) = 0 trong đó luỹ thừa của sinx và cosx cùng chẵn hoặc cùng lẻ.

Cách giải:

Xét cosx = 0 xem có là nghiệm của phương trình không?

Xét cosx ≠ 0. Chia hai vế phương trình cho cos^kx (k là số mũ cao nhất) ta được phương trình ẩn là tanx.

Giải và kết hợp nghiệm của cả hai trường hợp ta được nghiệm của phương trình đã cho.

Hoàn toàn tương tự ta có thể làm như trên đối với sinx.

Ví dụ minh họa

Bài 1: 3sin²x + 8sinx.cosx + (8√3-9) cos²x = 0 (1)

Xét cos⁡x = 0 ⇒ sin²x = 1. Ta có (1) ⇔ 3=0 (vô lý)

Xét cos⁡x≠0. Chia cả hai vế của pt cho cos²x. Ta được :

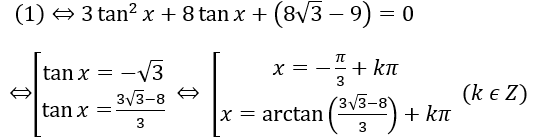
Bài 2: sin³x + 2sinx.cos²x + 3cos³x = 0 (2)

Xét cos⁡x = 0. Ta có (2) ⇔ sin⁡x = 0 (vô lí do sin²x + cos²x = 1)

Xét cos⁡x ≠ 0. Chia cả hai vế của pt cho cos³x. Ta được :

(2) ⇔ tan³⁡x + 2 tan⁡x + 3 = 0

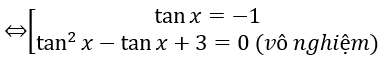
⇔ x = -π/4 + kπ (k ∈ Z)

B. Bài tập vận dụng

Bài 1: Giải phương trình sin² x-(√3+1)sinxcosx+√3 cos² x=0

Lời giải:

sin²⁡x - (√3+1) sin⁡x cos⁡x + √3 cos²⁡x = 0 (1)

Xét cos⁡x = 0. (1) sin²⁡x = 0 → vô lý

Xét cos⁡x≠0. Chia cả hai vế của pt cho cos²⁡x. Ta được :

(1) ⇔ tan²⁡x - (√3+1) tan⁡x + √3 = 0

Bài 2: Giải phương trình: 2 cos²x – 3sinxcosx + sin²x = 0

Lời giải:

Xét cos⁡x = 0. Ta có . sin²⁡x = 0 → vô lý

Xét cos⁡x ≠ 0. Chia cả hai vế của pt cho cos²⁡x. Ta được :

2 - 3 tan⁡x + tan²⁡x = 0

Bài 3: Giải phương trình: 3cos⁴x – 4cos²x sin²x + sin⁴x = 0

Lời giải:

Xét cos⁡x = 0: Ta có : sin⁴x = 0 (vô lý)

Xét cos⁡x ≠ 0. Chia cả hai vế của pt cho cos⁴x. Ta được :

3 - 4 tan²⁡x + tan⁴x = 0

Bài 4: Tìm m để phương trình (m + 1)sin²x – sin2x + 2cos²x = 0 có nghiệm.

Lời giải:

Xét cos⁡x = 0. Ta có : (m+1)sin²⁡x = 0 ⇔ m = -1

Xét cos⁡x ≠ 0. Chia cả hai vế của pt cho cos²⁡x. Ta được :

(m+1)tan²⁡x - 2 tan⁡x + 2 = 0

Δ' = 1-2m-2 = -2m-1

Để pt có nghiệm ⇔ Δ' ≥ 0 ⇔ - 2m-1 ≥ 0 ⇔ m ≤ -1/2

Vậy với m ≤ -1/2 thì pt đã cho có nghiệm

Bài 5: Tìm điều kiện để phương trình a.sin²x + a.sinxcosx + b.cos²x = 0 với a ≠ 0 có nghiệm.

Lời giải:

Xét cos⁡x ≠ 0. Chia cả hai vế của pt cho cos²⁡x. Ta được :

a tan²⁡x + atan⁡x + b = 0

Δ = a² - 4ab

Để pt có nghiệm ⇔ Δ' ≥ 0 ⇔a² - 4ab ≥ 0 ⇔ a-4b ≥ 0 ⇔ a ≥ 4b