Mở rộng phân số. Phân số bằng nhau lớp 6 (bài tập + lời giải)

---

Haylamdo biên soạn và sưu tầm chuyên đề phương pháp giải bài tập Mở rộng phân số. Phân số bằng nhau lớp 6 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Mở rộng phân số. Phân số bằng nhau.

Mở rộng phân số. Phân số bằng nhau lớp 6 (bài tập + lời giải)

Nhận biết phân số với tử số và mẫu số là các số nguyên

1. Phương pháp giải

- Với a, b ∈ ℤ, b ≠ 0, ta gọi $\frac{\text{a}}{\text{b}}$  là một phân số. Trong đó a là tử số (tử) và b là mẫu số (mẫu) của phân số.

- Mọi số nguyên đều viết được dưới dạng phân số với mẫu là 1.

2. Ví dụ minh họa

Ví dụ 1. Viết và đọc phân số trong trường hợp sau: Tử số là –4 và mẫu số là 3.

Hướng dẫn giải:

Ta viết được phân số là $\frac{-4}{3}$ .

Đọc là: âm bốn phần ba.

Ví dụ 2. $\frac{2}{11}$  có phải là phân số không? Nếu có hãy xác định tử và mẫu của phân số đó.

Hướng dẫn giải:

$\frac{2}{11}$ là một phân số vì tử số và mẫu số là các số nguyên và mẫu số khác 0.

Trong phân số trên 2 là tử số và 11 là mẫu số.

3. Bài tập tự luyện

Bài 1. Phép chia 8 : (–19) được viết dưới dạng phân số là:

A. $\frac{-19}{8}$ .

B. $\frac{8}{-19}$ .

C. $\frac{18}{-9}$ .

D. $\frac{-9}{18}$ .

Bài 2. Phép chia 79 : 3 được viết dưới dạng phân số là:

A. $\frac{3}{79}$ .

B. $\frac{97}{3}$ .

C. $\frac{79}{3}$ .

D. $\frac{-3}{79}$ .

Bài 3. Số –5 được viết dưới dạng phân số là:

A. $\frac{-5}{1}$ .

B. $\frac{1}{5}$ .

C. $\frac{-1}{5}$ .

D. $\frac{-5}{0}$ .

Bài 4. Phân số $\frac{-8}{10}$  đọc là:

A. Âm mười phần tám.

B. Mười phần tám.

C. Tám phần mười.

D. Âm tám phần mười.

Bài 5. Cách viết nào sau đây cho ta một phân số?

A. $\frac{6}{0,07}$ .

B. $\frac{-3,25}{81}$ .

C. $\frac{1}{0}$ .

D. $\frac{-52}{14}$ .

Bài 6. Phần tô màu biểu diễn phân số nào?

A. $\frac{10}{3}$ .

B. $\frac{3}{7}$ .

C. $\frac{3}{10}$ .

D. $\frac{3}{9}$ .

Bài 7. Cho phân số $\text{A}=\frac{30}{\text{n}-7}$  (n ∈ ℤ), tìm tất cả các giá trị của n để A là phân số.

A. n ≠ 7.

B. n = 7.

C. n = 30.

D. n ≠ 30.

Bài 8. Cho tập H = {6; 2; 7}. Có thể viết được tất cả bao nhiêu phân số có tử và mẫu thuộc tập H và tử khác mẫu?

A. 7.

B. 6.

C. 8.

D. 5.

Bài 9. Cho phân số $\text{B}=\frac{-1}{{\text{n}}^{\text{2}}+9}$  (n ∈ ℤ). Khẳng định nào sao đây là sai

A. Không có giá trị nào của n để B là phân số.

B. n = 0 thì B là phân số.

C. n = –5 thì B là phân số .

D. n = 100 thì B là phân số.

Bài 10. Tìm các số tự nhiên n để phân số $\frac{\text{n}+2}{\text{n}}$  có giá trị là số nguyên.

A. {–1; –2; 1; 2}.

B. {–1; 1}.

C. {1; 2}.

D. {–2; 2}.

Phân số bằng nhau

1. Phương pháp giải

Hai phân số $\frac{\text{a}}{\text{b}}\text{ và }\frac{\text{c}}{\text{d}}$  bằng nhau nếu a ⋅ d = b ⋅ c.

2. Ví dụ minh họa

Ví dụ 1. Phân số $\frac{11}{2}\text{ và }\frac{33}{6}$  có bằng nhau không?

Hướng dẫn giải:

Ta có $\frac{11}{2}=\frac{33}{6}$  vì 11 ⋅ 6 = 2 ⋅ 33 (= 66).

Ví dụ 2. Cặp phân số $\frac{1}{9}\text{ và }\frac{-1}{-9}$  có bằng nhau không?

Hướng dẫn giải:

Ta có $\frac{1}{9}=\frac{-1}{-9}$  vì 1 ⋅ (–9) = (–1) ⋅ 9      (= –9).

3. Bài tập tự luyện

Bài 1. Phân số nào dưới đây bằng với phân số $\frac{-3}{14}$ ?

A. $\frac{9}{42}$ .

B. $\frac{-9}{-42}$ .

C. $\frac{-6}{28}$ .

D. $\frac{6}{28}$ .

Bài 2. Chọn câu đúng

A. $\frac{5}{12}=\frac{10}{36}$ .

B. $\frac{-3}{7}=\frac{9}{-21}$ .

C. $\frac{-1}{-6}=\frac{-7}{42}$ .

D. $\frac{15}{2}=\frac{30}{8}$ .

Bài 3. Điền số thích hợp vào chỗ chấm $\frac{20}{3}=\frac{80}{\mathrm{....}}$ .

A. 12.

B. 22.

C. 21.

D. 11.

Bài 4. Số nguyên x thỏa mãn $\frac{\text{x}}{15}=\frac{20}{75}$  là:

A. 6.

B. 3.

C. 5.

D. 4.

Bài 5. Tìm các số nguyên x, y biết $\frac{-3}{4}=\frac{\text{x}}{24}=\frac{27}{\text{y}}$

A. x = –18, y = –36.

B. x = 18, y = –36.

C. x = –18, y = 36.

D. x = 18, y = 36.

Bài 6. Tổng các số x, y, z thỏa mãn $\frac{5}{7}=\frac{\text{x}}{49}=\frac{\text{y}}{-35}=\frac{45}{\text{z}}$  là:

A. 53.

B. 35.

C. 37.

D. 73.

Bài 7. Có bao nhiêu cặp số nguyên (x; y) thỏa mãn $\frac{\text{x}}{2}=\frac{1}{-\text{y}}$  ( x < 0 < y)?

A. 1.

B. 2.

C. 3.

D. 4.

Bài 8. Có thể lập được bao nhiêu cặp phân số bằng nhau từ bốn số sau: 2; 5; 15; 6?

A. 5.

B. 4.

C. 2.

D. 1.

Bài 9. Chọn khẳng định sai

A. Từ bốn số 2; 6; 3; 9 có thể lập được 4 cặp phân số bằng nhau.

B. Từ bốn số 4; 5; 3; 7 không thể lập được cặp phân số bằng nhau nào.

C. Từ bốn số 5; 7; 10; 14 có thể lập được 2 cặp phân số bằng nhau.

D. Từ bốn số 1; 2; 3; 4 không thể lập được cặp phân số bằng nhau nào.

Bài 10. Tìm các số nguyên x, y biết $\frac{x+7}{y+3}=\frac{7}{3}$  và x + y = 50.

A. (x; y) = (35; 15).

B. (x; y) = (15; 35).

C. (x; y) = (25; 15).

D. (x; y) = (15; 25).

Tính chất cơ bản của phân số

1. Phương pháp giải

- Tính chất 1: Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.

$\frac{\text{a}}{\text{b}}=\frac{\text{a}\cdot \text{m}}{\text{b}\cdot \text{m}}$ với m ∈ ℤ, m ≠ 0.

- Áp dụng tính chất 1 ta có thể thực hiện quy đồng mẫu các phân số bằng cách nhân cả tử và mẫu của phân số với số nguyên thích hợp.

- Tính chất 2: Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.

$\frac{\text{a}}{\text{b}}=\frac{\text{a : n}}{\text{b : n}}$ với n là ước chung của a và b.

- Áp dụng tính chất 2 ta có thể rút gọn phân số bằng cách chia cho ƯCLN.

- Chú ý: Ta có thể đưa dấu “ – ” ở dưới mẫu lên trên tử hoặc ra ngoài phân số.

$\frac{\text{a}}{-\text{b}}=\frac{-\text{a}}{\text{b}}=-\frac{\text{a}}{\text{b}}$.

2. Ví dụ minh họa

Ví dụ 1. Nhân cả tử và mẫu của phân số $\frac{11}{3}$  với 5 ta được phân số nào?

Hướng dẫn giải:

$\frac{11}{3}=\frac{11\cdot 5}{3\cdot 5}=\frac{55}{15}$

Khi đó ta được phân số mới là $\frac{55}{15}$  bằng phân số đã cho là $\frac{11}{3}$ .

Ví dụ 2. Phân số $\frac{80}{35}$  có thể rút gọn thành phân số nào?

Hướng dẫn giải:

Ta thấy ƯCLN của 80 và 35 là 5. Vậy ta chia cả tử và mẫu của phân số cho 5 được:

$\frac{80}{35}=\frac{80:5}{35:5}=\frac{16}{7}$

Vậy phân số $\frac{80}{35}$  có thể rút gọn thành phân số $\frac{16}{7}$ .

3. Bài tập tự luyện

Bài 1. Với a, b, m ∈ ℤ; m ≠ 0, n là ƯCLN của a và b. Khẳng định nào sau đây là đúng

A. $\frac{\text{a}}{\text{b}}=\frac{\text{a}-\text{m}}{\text{b}-\text{m}}$ .

B. $\frac{\text{a}}{\text{b}}=\frac{\text{a + m}}{\text{b}+\text{m}}$ .

C. $\frac{\text{a}}{\text{b}}=\frac{\text{a}\cdot \text{m}}{\text{b}\cdot \text{m }}$ .

D. $\frac{-\text{a}}{\text{b}}=\frac{\text{a : n}}{\text{b : n}}$.

Bài 2. Phân số $\frac{-16}{-4}$  bằng phân số nào?

A. 4.

B. –4.

C. $\frac{-4}{2}$ .

D. $\frac{4}{2}$ .

Bài 3. Nhân cả tử và mẫu của phân số $\frac{23}{5}$  với –1 ta được phân số mới là:

A. $\frac{-23}{5}$ .

B. $\frac{23}{-5}$ .

C. $-\frac{23}{5}$ .

D. $\frac{-23}{-5}$ .

Bài 4. Nhân cả tử và mẫu của phân số $\frac{2}{9}$  với số nào để được phân số $\frac{24}{108}$ ?

A. 9.

B. 10.

C. 12.

D. 14.

Bài 5. Trong các khẳng định sau, khẳng định nào là sai?

A. $\frac{-12}{39}=\frac{4}{-13}$ .

B. $\frac{4}{5}=\frac{28}{35}$ .

C. $\frac{48}{30}=\frac{16}{12}$ .

D. $\frac{13}{2}=\frac{26}{4}$ .

Bài 6. Cho $\frac{-8}{36}=\frac{\mathrm{....}}{9}$  số thích hợp điền vào chỗ chấm là:

A. –2.

B. 2.

C. 4.

D. –4.

Bài 7. Tìm x biết $\frac{1}{\text{x}}=\frac{6}{-18}$ .

A. 3.

B. –3.

C. 2.

D. –4.

Bài 8. Có thể biểu diễn số 7 ở dạng phân số có mẫu là –6 là:

A. $\frac{-7}{-6}$ .

B. $\frac{7}{-6}$ .

C. $\frac{-42}{-6}$ .

D. $-\frac{42}{6}$ .

Bài 9. Cho các phân số sau: $\frac{4}{9};\frac{8}{17};\frac{12}{27};\frac{8}{18};\frac{46}{108}$ . Các phân số bằng phân số $\frac{24}{54}$  là:

A. $\frac{4}{9};\frac{8}{17};\frac{12}{27};\frac{8}{18}$ .

B. $\frac{4}{9};\frac{12}{27};\frac{8}{18}$ .

C. $\frac{4}{9};\frac{8}{17};\frac{12}{27};\frac{46}{108}$ .

D. $\frac{12}{27};\frac{8}{18};\frac{46}{108}$ .

Bài 10. Viết một phân số mới bằng phân số $\frac{9}{8}$  sao cho tử số của phân số mới gấp 4 lần tử số của phân số cũ. Phân số đó là:

A. $\frac{9}{32}$ .

B. $\frac{36}{8}$ .

C. $\frac{32}{36}$ .

D. $\frac{36}{32}$ .

Rút gọn phân số

1. Phương pháp giải

- Muốn rút gọn phân số ta chia cả tử và mẫu của phân số đó cho cùng một ước chung (khác 1 và –1) của cả tử và mẫu số.

- Phân số tối giản là phân số mà tử số và mẫu số chỉ có ước chung là 1 và –1.

- Muốn rút gọn một phân số về phân số tối giản ta chia cả tử và mẫu của phân số đó cho ước chung lớn nhất của cả tử và mẫu số.

2. Ví dụ minh họa

Ví dụ 1. Rút gọn phân số $\frac{15}{50}$  về phân số tối giản.

Hướng dẫn giải:

Ta có ƯCLN(15,50) = 5 nên $\frac{15}{50}=\frac{15:5}{50:5}=\frac{3}{10}$

Rút gọn phân số $\frac{15}{50}$  ta được phân số tối giản là $\frac{3}{10}$ .

Ví dụ 2. Phân số $\frac{-5}{21}$  có phải là phân số tối giản không?

Hướng dẫn giải:

Ta có ƯCLN(–5, 21) = 1 nên phân số $\frac{-5}{21}$  là phân số tối giản.

3. Bài tập tự luyện

Bài 1. Sau khi rút gọn tối giản phân số $\frac{33}{27}$  ta được phân số nào?

A. $\frac{11}{9}$ .

B. $\frac{11}{27}$ .

C. $\frac{33}{9}$ .

D. $\frac{12}{9}$ .

Bài 2. Trong các phân số sau phân số nào là phân số tối giản?

A. $\frac{94}{10}$ .

B. $\frac{21}{60}$ .

C. $\frac{72}{56}$ .

D. $\frac{12}{31}$ .

Bài 3. Dùng phân số tối giản biểu diễn 40 phút theo giờ. Phân số đó là:

A. $\frac{\text{40}}{\text{60}}$ .

B. $\frac{\text{2}}{\text{3}}$ .

C. $\frac{\text{4}}{\text{6}}$ .

D. $\frac{\text{6}}{\text{4}}$ .

Bài 4. Rút gọn biểu thức A = $\frac{\text{23.12-23.2}}{\text{40 - 17}}$ ta được kết quả là:

A. 11.

B. 21.

C. 10.

D. 20.

Bài 5. Rút gọn biểu thức 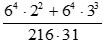 ta được kết quả là:

A. 3.

B. 4.

C. 5.

D. 6.

Bài 6. Bạn Lan có 20 quả bóng trong đó có 5 quả bóng vàng, 7 quả bóng xanh và còn lại là bóng trắng. Hỏi số bóng trắng chiếm bao nhiêu phần tổng số bóng?

A. $\frac{\text{5}}{\text{20}}$.

B. $\frac{\text{3}}{\text{5}}$.

C. $\frac{\text{2}}{\text{5}}$.

D. $\frac{\text{7}}{\text{20}}$.

Bài 7. Hùng có tất cả 120 viên bi. Hùng cho Hải 30 viên bi, cho Nam 40 viên bi và cho Phong 25 viên bi. Hỏi số bi còn lại của Hùng chiếm bao nhiêu phần tổng số bi ban đầu?

A. $\frac{\text{5}}{\text{12}}$.

B. $\frac{\text{5}}{\text{24}}$.

C. $\frac{\text{5}}{\text{6}}$.

D. $\frac{\text{1}}{\text{4}}$.

Bài 8. Tìm số nguyên x sao cho $\frac{\text{3}}{\text{x}}$ = $\frac{\text{x}}{\text{12}}$.

A. x ∈ {48}.

B. x ∈ {–6; 6}.

C. x ∈ {–6}.

D. x ∈ {6}.

Bài 9. Có bao nhiêu phân số bằng với phân số $\frac{\text{35}}{\text{98}}$ mà tử và mẫu số là các số có hai chữ số?

A. 5.

B. 4.

C. 6.

D. 2.

Bài 10.Phân số tối giản biểu diễn đại lượng 223 kg theo tấn là:

A. $\frac{\text{232}}{\text{1000}}$.

B. $\frac{\text{223}}{\text{10}}$.

C. $\frac{\text{223}}{\text{1000}}$.

D. $\frac{\text{223}}{\text{100}}$.