Nhận biết trục đối xứng và tâm đối xứng của một số hình phẳng cơ bản lớp 6 (bài tập + lời giải)
Haylamdo biên soạn và sưu tầm chuyên đề phương pháp giải bài tập Nhận biết trục đối xứng và tâm đối xứng của một số hình phẳng cơ bản lớp 6 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Nhận biết trục đối xứng và tâm đối xứng của một số hình phẳng cơ bản.
Nhận biết trục đối xứng và tâm đối xứng của một số hình phẳng cơ bản lớp 6 (bài tập + lời giải)
* Ta dựa vào dấu hiệu nhận biết trục đối xứng và tâm đối xứng của một số hình phẳng cơ bản để giải quyết bài toán.
* Trục đối xứng của một số hình học cơ bản:
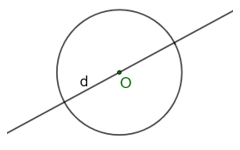
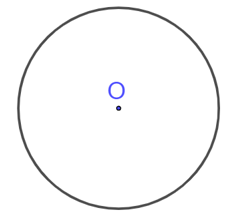
- Hình tròn: Mỗi đường thẳng đi qua tâm là trục đối xứng của hình tròn.
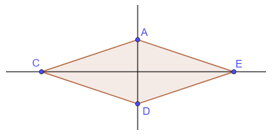
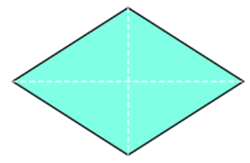
- Hình thoi: Mỗi đường chéo là một trục đối xứng của hình thoi.
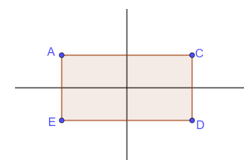
- Hình chữ nhật: Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.
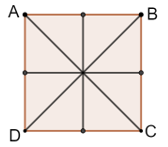
- Hình vuông: Mỗi đường thẳng đi qua trung điểm hai cạnh đôi diện, mỗi đường chéo là một trục đối xứng của hình vuông.
- Hình lục giác đều: Trục đối xứng của hình lục giác đều là các đường thẳng đi qua một cặp đỉnh đối diện và các đường thẳng đi qua các trung điểm của một cặp cạnh đối diện.
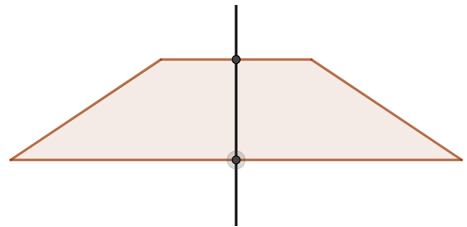
- Hình thang cân: Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm của hai đáy.
* Tâm đối xứng của một số hình học cơ bản:
- Tâm đối xứng của hình tròn chính là tâm của đường tròn đó.
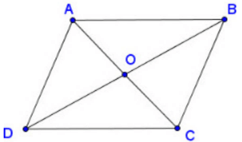
- Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.
-Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
2. Ví dụ minh họa:
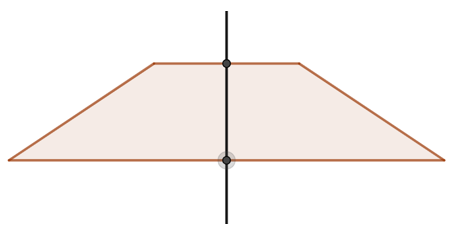
Ví dụ 1. Hãy chỉ ra trục đối xứng của hình thang cân.
Hướng dẫn giải:
Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm của hai đáy.
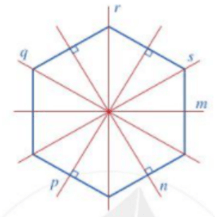
Ví dụ 2. Hình lục giác đều có bao nhiêu trục đối xứng?
Hướng dẫn giải:
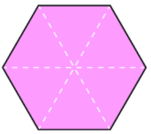
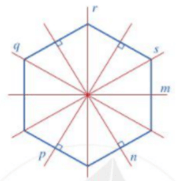
Trục đối xứng của hình lục giác đều là các đường thẳng đi qua một cặp đỉnh đối diện và các đường thẳng đi qua các trung điểm của một cặp cạnh đối diện.
Ta có hình vẽ sau:
Vậy hình lục giác đều có 6 trục đối xứng.
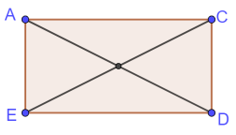
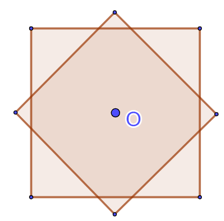
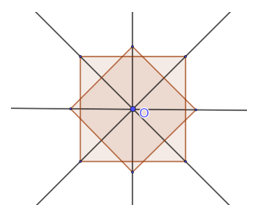
Ví dụ 3. Trong hình vẽ dưới đây, điểm O có phải là tâm đối xứng không?
Hướng dẫn giải:
Ta thấy O chính là tâm đối xứng ở hình vuông nằm phía dưới, bên cạnh đấy hình thoi ở phía trên cũng có O là tâm đối xứng nên O chính là tâm đối xứng của hình bên.
Hình vẽ minh họa:
3. Bài tập tự luyện
Bài 1. Hình nào dưới đây có vô số trục đối xứng?
A. Hình lục giác đều;
B. Hình tròn;
C. Hình chữ nhật;
D. Hình thoi.
Bài 2. Hãy chọn đáp án đúng. Trục đối xứng của hình thang cân là?
A. Đường thẳng đi qua trung điểm hai cạnh đáy của hình thang cân;
B. Đường thẳng đi qua trung điểm hai cạnh bên của hình thang cân;
C. Đường chéo của hình thang cân;
D. Đường thẳng vuông góc với hai cạnh đáy.
Bài 3. Trong các hình sau: hình tròn, hình chữ nhật, hình thoi, hình vuông, hình lục giác đều thì có bao nhiêu hình có 2 trục đối xứng?
A. 1;
B. 4;
C. 6;
D. 2.
Bài 4. Phát biểu nào sau đây là đúng?
A. Tam giác cân có 2 trục đối xứng;
B. Tam giác đều có 3 trục đối xứng;
C. Hình tam giác có 3 trục đối xứng;
D. Hình thang cân có 2 trục đối xứng.
Bài 5. Đoạn thẳng AB có độ dài bằng 6cm. Gọi O là tâm đối xứng của đoạn thẳng AB. Tính độ dài đoạn thẳng OA?
A. 2cm;
B. 3cm;
C. 5cm;
D. 6cm.
Bài 6. Tâm đối xứng của hình tròn là?
A. Một điểm bất kì nằm trên hình tròn;
B. Tâm hình tròn;
C. Một điểm bất kì nằm trong hình tròn;
D. Một điểm bất kì nằm ngoài hình tròn.
Bài 7. Tâm đối xứng của hình chữ nhật là:
A. Hình chữ nhật không có tâm đối xứng;
B. Giao điểm của hai đường thẳng nối trung điểm của các cạnh đối diện với nhau;
C. Giao điểm của hai đường chéo;
D. Tất cả các đáp án trên đều sai.
Bài 8. Trong các hình dưới đây hình nào không có tâm đối xứng?
A. Hình lục giác đều;
B. Hình chữ nhật;
C. Hình thoi;
D. Tam giác đều.
Bài 9. Phát biểu nào dưới đây đúng?
A. Hình thoi có tâm đối xứng nhưng không có trục đối xứng;
B. Hình chữ nhật có trục đối xứng nhưng không có tâm đối xứng;
C. Hình thang cân có trục đối xứng vừa có tâm đối xứng;
D. Hình lục giác đều vừa có trục đối xứng vừa có tâm đối xứng.
Bài 10. Trong các hình sau: hình tròn, hình chữ nhật, hình thoi, hình bình hành, hình lục giác đều, hình thang cân, hình tam giác đều, có bao nhiêu hình có không có tâm đối xứng?
A. 0;
B. 1;
C. 2;
D. 3.