Xét tính chia hết của một tổng các lũy thừa cùng cơ số lớp 6 (bài tập + lời giải)

---

Haylamdo biên soạn và sưu tầm chuyên đề phương pháp giải bài tập Xét tính chia hết của một tổng các lũy thừa cùng cơ số lớp 6 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Xét tính chia hết của một tổng các lũy thừa cùng cơ số.

Xét tính chia hết của một tổng các lũy thừa cùng cơ số lớp 6 (bài tập + lời giải)

1. Phương pháp giải

Để xét tính chia hết của một tổng các lũy thừa cùng cơ số, ta làm như sau:

a) Biến đổi, nhóm các hạng tử thích hợp để tìm ra nhân tử chung.

b) Áp dụng tính chất chia hết của một tổng:

 

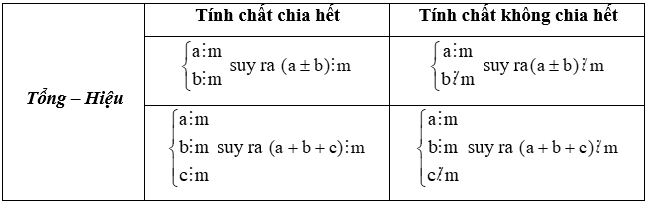
2. Ví dụ minh họa

Ví dụ 1. Cho A = 2 + 2² + 2³ + 2⁴. Hỏi A có chia hết cho 3 không?

Hướng dẫn giải:

A = 2 + 2² + 2³ + 2⁴

= (2 + 2²) + (2³ + 2⁴)

= 2. (1 + 2) + 2³. (1 + 2)

= 2.3 + 2³.3

= 3. (2 + 2³)

Vì 3 $⋮$3 nên 3. (2 + 2³) $⋮$3

Vậy A = 2 + 2² + 2³ + 2⁴ chia hết cho 3.

Ví dụ 2. Cho B = 2 + 2³ + 2⁵ + 2⁷ + … + 2⁹⁹. Chứng minh rằng B chia hết cho 10.

Hướng dẫn giải:

B = 2 + 2³ + 2⁵ + 2⁷ + … + 2⁹⁹

= 2. (1 + 2² + 2⁴ + 2⁶ + … + 2⁹⁸)

Vì 2. (1 + 2² + 2⁴ + 2⁶ + … + 2⁹⁸) chia hết cho 2 nên B chia hết cho 2

B = 2 + 2³ + 2⁵ + 2⁷ + … + 2⁹⁹

= (2 + 2³) + (2⁵ + 2⁷) + … + (2⁹⁷ + 2⁹⁹)

= 2. (1 + 2²) + 2⁵. (1 + 2²)  + … + 2⁹⁷. (1 + 2²)

= 2.5 + 2⁵.5 + … + 2⁹⁷.5

= 5. (2 + 2⁵ + … + 2⁹⁷)

Vì 5 $⋮$5 nên 5. (2 + 2⁵ + … + 2⁹⁷) $⋮$5

Do đó B chia hết cho 5

B chia hết cho cả 2 và 5 nên B chia hết cho 10.

Ví dụ 3. Số dư của phép chia A = 2 + 2² + 2³ + … + 2⁶⁰ cho 3 là bao nhiêu?

Hướng dẫn giải:

A = 2 + 2² + 2³ + … + 2⁶⁰

= (2 + 2²) + (2³ + 2⁴) + … + (2⁵⁹ + 2⁶⁰)

= 2. (1 + 2) + 2³. (1 + 2) + … + 2⁵⁹. (1 + 2)

= 2.3 + 2³.3 + … + 2⁵⁹.3

= 3. (2 + 2³ + … + 2⁵⁹)

Vì 3 $⋮$3 nên 3. (2 + 2³ + … + 2⁵⁹) $⋮$3

Suy ra A = 2 + 2² + 2³ + 2⁴ chia hết cho 3.

Vậy số dư của phép chia A = 2 + 2² + 2³ + … + 2⁶⁰ cho 3 là 0.

3. Bài tập tự luyện

Bài 1. Cho A = 16⁵ + 2¹⁵. Vậy A chia hết cho:

A. 30;

B. 33;

C. 32;

D. 31.

Bài 2. Cho B = 3 + 3² + 3³ + 3⁴. Vậy B chia hết cho:

A. 4;

B. 9;

C. 11;

D. 7.

Bài 3. Cho M = 5 + 5² + 5³ + 5⁴ + 5⁵ + 5⁶. Vậy M chia hết cho:

A. 33;

B. 36;

C. 31;

D. 56.

Bài 4. Cho C = 2 + 2² + 2³ + … + 2²⁰¹⁰. Vậy C chia hết cho:

A. 7;

B. 11;

C. 13;

D. 19.

Bài 5. Cho D = 3 + 3² + 3³ + … + 3²⁰¹². Vậy D chia hết cho:

A. 7;

B. 11;

C. 13;

D. 40.

Bài 6. Cho S = 3⁰ + 3² + 3⁴ + 3⁶ + … + 3²⁰⁰². Vậy S chia hết cho:

A. 3;

B. 7;

C. 9;

D. 5.

Bài 7. Số dư khi chia S = 3² + 3³ + 3⁴ + 3⁵ + … + 3²⁰²¹ cho 13 là:

A. 3;

B. 6;

C. 9;

D. 11.

Bài 8. Cho A = 1 + 4 + 4² + 4³ + 4⁴ + 4⁵ + … + 4⁶⁰. Số dư của A khi chia cho 21 là:

A. 1;

B. 2;

C. 3;

D. 4.

Bài 9. Cho B = 2 + 2² + 2³ + 2⁴ + … + 2¹⁰⁰. Chữ số tận cùng của B là:

A. 2;

B. 6;

C. 4;

D. 0.

Bài 10. Cho C = 1 + 2 + 2² + 2³ + 2⁴ + … + 2¹¹. Số dư của phép chia C khi chia cho 9 là:

A. 0;

B. 1;

C. 2;

D. 3.