Cho tam giác ABC vuông tại A. Gọi D là điểm thuộc cạnh BC

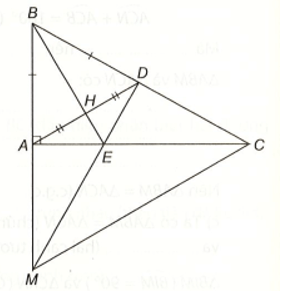
Cho tam giác ABC vuông tại A. Gọi D là điểm thuộc cạnh BC sao cho BD = BA và H là trung điểm của AD. Tia BH cắt AC tại E. Tia DE cắt tia BA tại M. Chứng minh rằng:

Giải vở thực hành Toán 7 Bài tập ôn tập cuối năm

Bài 10 trang 110 vở thực hành Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A. Gọi D là điểm thuộc cạnh BC sao cho BD = BA và H là trung điểm của AD. Tia BH cắt AC tại E. Tia DE cắt tia BA tại M. Chứng minh rằng:

a) ∆ABH = ∆DBH.

b) Tam giác AED cân.

c) EM > ED.

d) Tam giác BCM là tam giác đều và CE = 2EA, biết $\widehat{ABC}$ = 60°.

Lời giải:

a) ∆ABH và ∆DBH có:

BA = BD (theo giả thiết),

BH là cạnh chung,

AH = DH (H là trung điểm của AD).

Nên ∆ABH = ∆DBH (c.c.c).

b) ∆ABH = ∆DBH (chứng minh trên), suy ra $\widehat{ABE}=\widehat{DBE}$ (hai góc tương ứng).

∆BAE và ∆BDE có:

BA = BD (giả thiết),

$\widehat{ABE}=\widehat{DBE}$ (chứng minh trên),

BE là cạnh chung.

Nên ∆BAE = ∆BDE  (c.g.c) suy ra EA = ED (hai cạnh tương ứng).

Nên ∆AED cân tại E (dấu hiệu nhận biết tam giác cân).

c) ∆BAE = ∆BDE (chứng minh trên) nên $\widehat{BDE}=\widehat{BAE}=90°$.

∆EAM và ∆EDC có:

          $\widehat{EAM}=\widehat{EDC}=90°$,

          EA = ED (chứng minh trên),

         $\widehat{AEM}=\widehat{DEC}$ (hai góc đối đỉnh).

Nên ∆EAM = ∆EDC (g.c.g). Suy ra EM = EC.

∆EDC vuông tại D nên EC > ED (quan hệ giữa cạnh và góc trong tam giác).

Mà EC = EM (chứng minh trên) nên EM > ED.

d) Ta có ∆EAM = ∆EDC (chứng minh trên), suy ra AM = DC (hai cạnh tương ứng).

Mà BA = BD (giả thiết) nên BM = BC.

∆BMC có: BM = BC (chứng minh trên).

Nên ∆BMC cân tại B (dấu hiệu nhận biết tam giác cân).

Mà $\widehat{ABC}$ = 60° (giả thiết). Nên ∆BMC là tam giác đều.

Mặt khác CA ⊥ BM nên CA là đường cao nên cũng là đường trung tuyến của ∆BMC,

                MD ⊥ BC nên MD là đường cao nên cũng là đường trung tuyến của ∆BMC.

Từ đó suy ra E là trọng tâm của ∆BMC nên CE = 2EA.