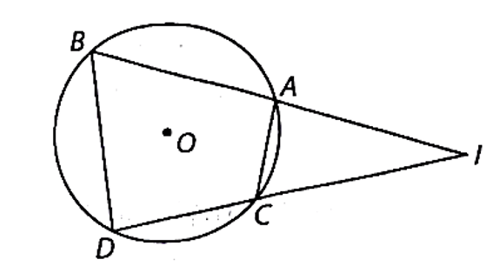
Cho điểm I nằm ngoài đường tròn (O). Qua I kẻ hai đường thẳng lần lượt cắt (O) tại bốn điểm
Cho điểm I nằm ngoài đường tròn (O). Qua I kẻ hai đường thẳng lần lượt cắt (O) tại bốn điểm A, B và C, D sao cho A nằm giữa B và I, C nằm giữa D và I. Chứng minh rằng và IA.IB = IC.ID.
Giải vở thực hành Toán 9 Bài 29: Tứ giác nội tiếp - Kết nối tri thức
Bài 2 trang 99 VTH Toán 9 Tập 2: Cho điểm I nằm ngoài đường tròn (O). Qua I kẻ hai đường thẳng lần lượt cắt (O) tại bốn điểm A, B và C, D sao cho A nằm giữa B và I, C nằm giữa D và I. Chứng minh rằng và IA.IB = IC.ID.
Lời giải:
Do tổng các góc nội tiếp của tứ giác nội tiếp ABCD bằng 360° nên:
Mặt khác, từ các đẳng thức trên ta suy ra ∆IBD ᔕ ∆ICA (g.g).
Do đó hay IA.IB = IC.ID.
Lời giải vở thực hành Toán 9 Bài 29: Tứ giác nội tiếp hay khác: