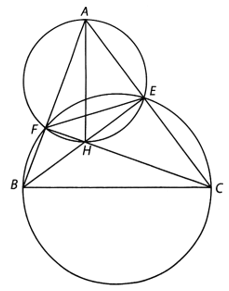
Cho tam giác nhọn ABC có các đường cao BE, CF cắt nhau tại H. Chứng minh rằng
Cho tam giác nhọn ABC có các đường cao BE, CF cắt nhau tại H. Chứng minh rằng:
Giải vở thực hành Toán 9 Bài 29: Tứ giác nội tiếp - Kết nối tri thức
Bài 8 trang 101 VTH Toán 9 Tập 2: Cho tam giác nhọn ABC có các đường cao BE, CF cắt nhau tại H. Chứng minh rằng:
a)
b)
Lời giải:
a) Ta có:
Do vậy các tam giác vuông BFC và BEC cùng nội tiếp đường tròn đường kính BC.
Suy ra tứ giác BCEF nội tiếp đường tròn đường kính BC.
Vì và là hai góc nội tiếp của tứ giác này và cùng chắn cung CE nên
Suy ra
Tương tự ta có:
b) Ta có:
Do vậy các tam giác vuông AEH và AFH cùng nội tiếp đường tròn đường kính AH.
Suy ra tứ giác AEFH nội tiếp đường tròn đường kính AH. Do và là hai góc đối nhau của tứ giác nội tiếp AEHF nên:
Suy ra
Tương tự
Vậy
Lời giải vở thực hành Toán 9 Bài 29: Tứ giác nội tiếp hay khác: