Kí hiệu (d1) là đường thẳng x + 2y = 4, (d2) là đường thẳng x – y = 1

Kí hiệu (d) là đường thẳng x + 2y = 4, (d) là đường thẳng x – y = 1

Giải vở thực hành Toán 9 Bài tập ôn tập cuối năm - Kết nối tri thức

Bài 5 trang 127 VTH Toán 9 Tập 2: Kí hiệu (d₁) là đường thẳng x + 2y = 4, (d₂) là đường thẳng x – y = 1

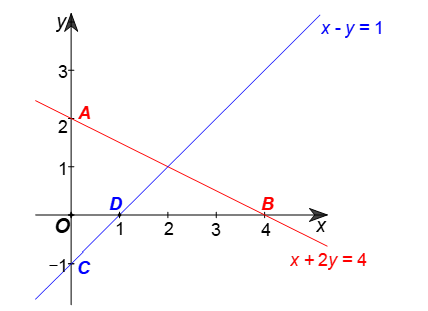
a) Vẽ (d₁) và (d₂) trên cùng một mặt phẳng toạ độ.

b) Giải hệ phương trình $\{\begin{cases} x + 2 y = 4 \\ x - y = 1 \end{cases}$ để tìm toạ độ giao điểm của hai đường thẳng (d₁) và (d₂).

Lời giải:

a) ⦁ Vẽ đường thẳng (d₁): x + 2y = 4.

Cho x = 0 thì y = 2, ta được giao điểm của đường thẳng (d₁) với trục tung là A(0; 2).

Cho y = 0 thì x = 4, ta được giao điểm của đường thẳng (d₁) với trục hoành là B(4; 0).

Đường thẳng (d₁) là đường thẳng AB (hình vẽ).

⦁ Vẽ đường thẳng (d₂): x – y = 1.

Cho x = 0 thì y = –1, ta được giao điểm của đường thẳng (d₂) với trục tung là C(0; –1).

Cho y = 0 thì x = 1, ta được giao điểm của đường thẳng (d₂) với trục hoành là D(1; 0).

Đường thẳng (d₂) là đường thẳng CD (hình vẽ).

Kí hiệu (d1) là đường thẳng x + 2y = 4, (d2) là đường thẳng x – y = 1

b) Giải hệ phương trình $\{\begin{cases} x + 2 y = 4 (1) \\ x - y = 1 (2) \end{cases}$

Trừ từng vế của hai phương trình (1) và (2), ta được:

(x + 2y) – (x – y) = 4 – 1 hay 3y = 3, suy ra y = 1.

Thế y = 1 vào phương trình (2), ta được:

x – 1 = 1 hay x = 2.

Do đó hệ phương trình trên có nghiệm là (2; 1).

Vậy toạ độ giao điểm của hai đường thẳng (d₁) và (d₂) là điểm (2; 1).

Lời giải vở thực hành Toán 9 Bài tập ôn tập cuối năm hay khác: