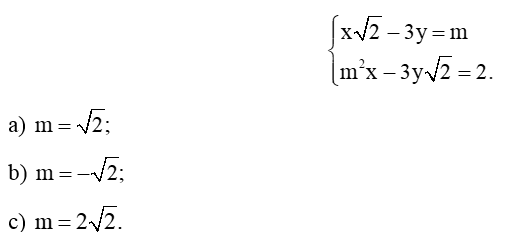Với mỗi giá trị đã cho của m, hãy giải hệ phương trình sau trang 127 VTH Toán 9 Tập 2

Với mỗi giá trị đã cho của m, hãy giải hệ phương trình sau:

Giải vở thực hành Toán 9 Bài tập ôn tập cuối năm - Kết nối tri thức

Bài 6 trang 127 VTH Toán 9 Tập 2: Với mỗi giá trị đã cho của m, hãy giải hệ phương trình sau:

Lời giải:

a) Với $m = \sqrt{2},$ ta có hệ phương trình: $(I) \{\begin{cases} x \sqrt{2} - 3 y = \sqrt{2} (1) \\ 2 x - 3 y \sqrt{2} = 2 \end{cases}$

Nhân hai vế của phương trình (1) với $\sqrt{2},$ ta được hệ phương trình sau:

$\{\begin{cases} 2 x - 3 y \sqrt{2} = 2 \\ 2 x - 3 y \sqrt{2} = 2. \end{cases}$

Trừ từng vế hai phương trình của hệ mới, ta được:

0x + 0y = 0. Hệ thức này luôn thỏa mãn với các giá trị tùy ý của x và y.

Với giá trị tùy ý của x, giá trị của y được tính nhờ hệ thức $x \sqrt{2} - 3 y = \sqrt{2},$ suy ra $y = \frac{\sqrt{2}}{3} x - \frac{\sqrt{2}}{3} .$

Vậy hệ phương trình (I) có nghiệm là $(x; \frac{\sqrt{2}}{3} x - \frac{\sqrt{2}}{3})$ với x ∈ ℝ.

b) Với $m = - \sqrt{2},$ ta có hệ phương trình: $(I I) \{\begin{cases} x \sqrt{2} - 3 y = - \sqrt{2} (2) \\ 2 x - 3 y \sqrt{2} = 2 \end{cases}$

Nhân hai vế của phương trình (2) với $\sqrt{2}$ ta được hệ phương trình sau:

$\{\begin{cases} 2 x - 3 y \sqrt{2} = - 2 \\ 2 x - 3 y \sqrt{2} = 2. \end{cases}$

Trừ từng vế hai phương trình của hệ mới, ta được:

0x + 0y = –4. Phương trình này vô nghiệm.

Vậy hệ phương trình (II) vô nghiệm.

c) Với $m = 2 \sqrt{2},$ ta có hệ phương trình: $(I I I) \{\begin{cases} x \sqrt{2} - 3 y = 2 \sqrt{2} (3) \\ 8 x - 3 y \sqrt{2} = 2 \end{cases}$

Nhân hai vế của phương trình (3) với $\sqrt{2}$ ta được hệ phương trình sau:

$\{\begin{cases} 2 x - 3 y \sqrt{2} = 4 \\ 8 x - 3 y \sqrt{2} = 2 \end{cases}$

Trừ từng vế hai phương trình của hệ mới, ta được:

–6x = 2, suy ra $x = - \frac{1}{3} .$

Thế $x = - \frac{1}{3}$ vào phương trình (3), ta được:

$- \frac{1}{3} \cdot \sqrt{2} - 3 y = 2 \sqrt{2},$ suy ra $3 y = - \frac{\sqrt{2}}{3} - 2 \sqrt{2},$ nên

$y = - \frac{\sqrt{2}}{9} - \frac{2 \sqrt{2}}{3} = \frac{- \sqrt{2} - 2 \sqrt{2} \cdot 3}{9} = \frac{- 7 \sqrt{2}}{9} .$

Vậy hệ phương trình (III) có nghiệm là $(- \frac{1}{3}; \frac{- 7 \sqrt{2}}{9}) .$

Lời giải vở thực hành Toán 9 Bài tập ôn tập cuối năm hay khác: