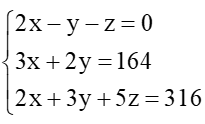Bài 8 trang 22 Chuyên đề Toán 10

Giải Chuyên đề Toán 10 Bài 2: Ứng dụng hệ phương trình bậc nhất ba ẩn

Haylamdo biên soạn và sưu tầm lời giải Bài 8 trang 22 Chuyên đề Toán 10 trong Bài 2: Ứng dụng hệ phương trình bậc nhất ba ẩn. Với lời giải chi tiết nhất hy vọng sẽ giúp học sinh biết cách làm bài tập Chuyên đề Toán 10.

Bài 8 trang 22 Chuyên đề Toán 10: Ba lớp 10A, 10B, 10C trồng được 164 cây bạch đàn và 316 cây thông. Mỗi học sinh lớp 10A trồng được 3 cây bạch đàn và 2 cây thông; mỗi học sinh lớp 10B trồng được 2 cây bạch đàn và 3 cây thông; mỗi học sinh lớp 10C trồng được 5 cây thông. Hỏi mỗi lớp có bao nhiêu học sinh? Biết số học sinh lớp 10A bằng trung bình cộng số học sinh lớp 10B và 10C.

Lời giải:

Gọi số học sinh của ba lớp 10A, 10B, 10C lần lượt là x, y, z (học sinh) (x, y, z $\in$ ℕ^*).

Theo đề bài ta có:

– Số học sinh lớp 10A bằng trung bình cộng số học sinh lớp 10B và 10C, suy ra:

x = $\frac{y+z}{2}\Rightarrow$ 2x – y – z = 0 (1).

– Số cây bạch đàn mỗi học sinh lớp 10A, 10B trồng được lần lượt là: 3, 2. Suy ra:

3x + 2y = 164 (2).

– Số cây thông mỗi học sinh lớp 10A, 10B, 10C trồng được lần lượt là: 2, 3, 5. Suy ra:

2x + 3y + 5z = 316 (3).

Từ (1), (2) và (3) ta có hệ phương trình:

Giải hệ này ta được x = 32, y = 34, z = 30 (thoả mãn điều kiện).

Vậy số học sinh của ba lớp 10A, 10B, 10C lần lượt là 32, 34, 30 học sinh.