Khám phá 2 trang 52 Chuyên đề Toán 10

Giải Chuyên đề Toán 10 Bài 2: Hypebol

Haylamdo biên soạn và sưu tầm lời giải Khám phá 2 trang 52 Chuyên đề Toán 10 trong Bài 2: Hypebol. Với lời giải chi tiết nhất hy vọng sẽ giúp học sinh biết cách làm bài tập Chuyên đề Toán 10.

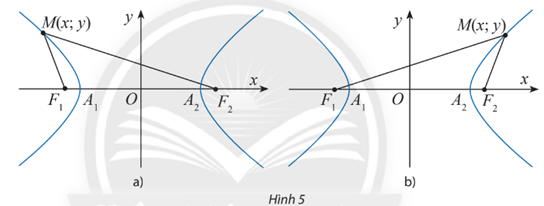
Khám phá 2 trang 52 Chuyên đề Toán 10: Cho điểm M(x; y) nằm trên hypebol $\left(H\right):\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

a) Chứng minh rằng F₁M² – F₂M² = 4cx.

b) Giả sử điểm M(x; y) thuộc nhánh đi qua A₁(–a; 0) (Hình 5a). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất MF₂ – MF₁ = 2a đã biết để chứng minh $F_2+M{F}_1=-2\frac{cx}{a}$. Từ đó, chứng minh các công thức: $F_1=-a-\frac{c}{a}x$; $F_2=a-\frac{c}{a}x.$

c) Giả sử điểm M(x; y) thuộc nhánh đi qua A₂(a; 0) (Hình 5 b). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất MF₁ – MF₂ = 2a đã biết để chứng minh $F_2+M{F}_1=2\frac{cx}{a}$. Từ đó, chứng minh các công thức: $F_1=a+\frac{c}{a}x$; $F_2=-a+\frac{c}{a}x.$

Lời giải:

a) F₁M² = [x – (– c)]² + (y – 0)² = (x + c)² + y² = x² + 2cx + c² + y²;

F₂M² = (x – c)² + (y – 0)² = x² – 2cx + c² + y².

F₁M² – F₂M² = (x² + 2cx + c² + y²) – (x² – 2cx + c² + y²) = 4cx.

b) Ta có: MF₁² – MF₂² = 4cx $\Rightarrow$ (MF₁ + MF₂)(MF₁ – MF₂) = 4cx $\Rightarrow$ (MF₁ + MF₂)(–2a) = 4cx

$\Rightarrow$ MF₁ + MF₂ = $\frac{4cx}{2a}$ = –$\frac{2c}{a}$x. Khi đó:

(MF₁ + MF₂) + (MF₁ – MF₂) = –$\frac{2c}{a}x$ + (–2a) $\Rightarrow$ 2MF₁ = –$\frac{2c}{a}x$ – 2a

$\Rightarrow$ MF₁ = $-(\frac{c}{a}x+a)$$=-a-\frac{c}{a}x.$

(MF₁ + MF₂) – (MF₁ – MF₂) = –$\frac{2c}{a}x$– (–2a) $\Rightarrow$ 2MF₂ = –$\frac{2c}{a}x$ + 2a

$\Rightarrow$ MF₂ = a –$\frac{c}{a}$x.

c) Ta có: MF₁² – MF₂² = 4cx $\Rightarrow$ (MF₁ + MF₂)(MF₁ – MF₂) = 4cx $\Rightarrow$ (MF₁ + MF₂)2a = 4cx

$\Rightarrow$ MF₁ + MF₂ = $\frac{4cx}{2a}$ = $\frac{2c}{a}x$. Khi đó:

(MF₁ + MF₂) + (MF₁ – MF₂) = $\frac{2c}{a}x$ + 2a $\Rightarrow$ 2MF₁ = $\frac{2c}{a}x$ + 2a

$\Rightarrow$ MF₁ = a + $\frac{c}{a}$x.

(MF₁ + MF₂) – (MF₁ – MF₂) = $\frac{2c}{a}x$ – 2a $\Rightarrow$ 2MF₂ = $\frac{2c}{a}x$– 2a

$\Rightarrow$MF₂ = – a + $\frac{c}{a}$x.