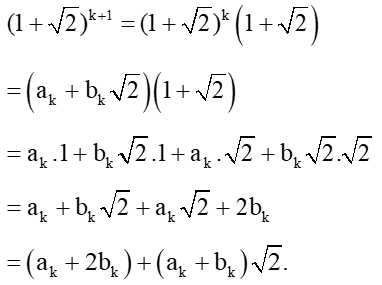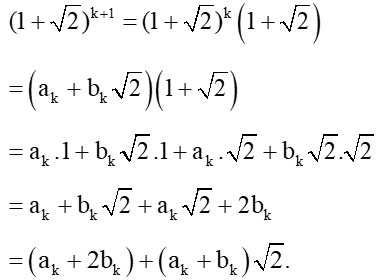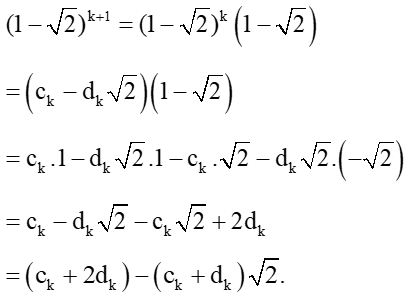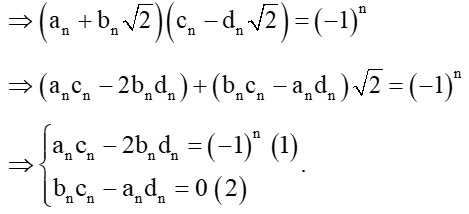Luyện tập 2 trang 26 Chuyên đề Toán 10

---

Giải Chuyên đề Toán 10 Bài 1: Phương pháp quy nạp toán học

Haylamdo biên soạn và sưu tầm lời giải Luyện tập 2 trang 26 Chuyên đề Toán 10 trong Bài 1: Phương pháp quy nạp toán học. Với lời giải chi tiết nhất hy vọng sẽ giúp học sinh biết cách làm bài tập Chuyên đề Toán 10.

Luyện tập 2 trang 26 Chuyên đề Toán 10: Chứng minh với mọi n ∈ ℕ^*,${(1+\sqrt{2})}^n$, ${(1-\sqrt{2})}^n$ lần lượt viết được ở dạng $a_n+b_n\sqrt{2},$$a_n-b_n\sqrt{2}$ , trong đó a_n, b_n là các số nguyên dương.

Lời giải:

+) Khi n = 1, ta có:

${(1+\sqrt{2})}^1=1+\sqrt{2}=1+1.\sqrt{2}\Rightarrow$a₁ = 1, b₁ = 1.

Vậy mệnh đề đúng với n = 1.

+) Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: ${(1+\sqrt{2})}^{k+1}$ viết được dưới dạng $a_{k+1}+b_{k+1}\sqrt{2},$ trong đó a_{k + 1}, b_{k + 1} là các số nguyên dương.

Thật vậy, theo giả thiết quy nạp ta có:

${(1+\sqrt{2})}^k=a_k+b_k\sqrt{2},$ với a_k, b_k là các số nguyên dương.

Khi đó:

Vì a_k, b_k là các số nguyên dương nên a_k + 2b_k và a_k + b_k cũng là các số nguyên dương.

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ^*.

+) Theo chứng minh trên ta có:

Với mọi n ∈ ℕ^* thì ${(1+\sqrt{2})}^n$= $a_n-b_n\sqrt{2}$ với a_n, b_n là các số nguyên dương.

Chứng minh tương tự ta được:

Với mọi n ∈ ℕ^* thì ${(1-\sqrt{2})}^n$ = $c_n-d_n\sqrt{2}$ với c_n, d_n là các số nguyên dương.

Giờ ta chứng minh a_n = c_n và b_n = d_n với mọi n ℕ^*.

Cách 1:

Xét mệnh đề P(n): a_n = c_n và b_n = d_n với mọi n ∈ ℕ^*.

+) Khi n = 1, ta có:

${(1+\sqrt{2})}^1=1+\sqrt{2}=1+1.\sqrt{2}\Rightarrow$ a₁ = 1, b₁ = 1.

${(1-\sqrt{2})}^1=1-\sqrt{2}=1-1.\sqrt{2}\Rightarrow$ c₁ = 1, d₁ = 1.

Vậy a₁ = c₁, b₁ = d₁.

Vậy mệnh đề P(n) đúng với n = 1.

+) Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề P(n) cũng đúng với k + 1, tức là: a_{k + 1} = c_{k + 1} và b_{k + 1} = d_{k + 1}.

Thật vậy, theo giả thiết quy nạp ta có: a_k = c_k và b_k = d_k (1).

Mặt khác:

a_{k + 1} = a_k + 2b_k, b_{k + 1} = a_k + b_k (2).

nên c_{k + 1} = c_k + 2d_k, d_{k + 1} = c_k + d_k (3)

Từ (1), (2) và (3) ta suy ra a_{k + 1} = c_{k + 1} và b_{k + 1} = d_{k + 1}.

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ^*.

Vậy bài toán đã được chứng minh.

Cách 2:

Ta có:

${(1+\sqrt{2})}^n{\left(1-\sqrt{2}\right)}^n={\left[\left(1+\sqrt{2}\right)\left(1-\sqrt{2}\right)\right]}^n={\left(-1\right)}^n$

Từ (2) ta suy ra $a_n{d}_n=b_n{c}_n\Rightarrow \frac{a_n}{c_n}=\frac{b_n}{d_n}=k$ với k > 0 (vì a_n, b_n, c_n, d_n là các số nguyên dương)

$\Rightarrow a_n=k{c}_n,b_n=k{d}_n.$ Thế vào (1) ta được:

$\left(k{c}_n\right)c_n-2\left(k{d}_n\right)d_n={\left(-1\right)}^n\Rightarrow k\left(c_n^2-2d_n^2\right)={\left(-1\right)}^n$

$\Rightarrow 1⋮k\Rightarrow k=1\Rightarrow$a_n = c_n và b_n = d_n.

Vậy ta có điều phải chứng minh.