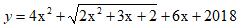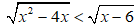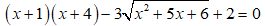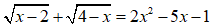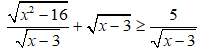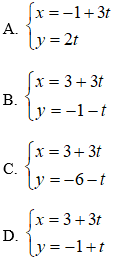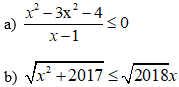Bộ Đề thi Toán lớp 10 Học kì 2 năm 2023 (15 đề)

---

Bộ Đề thi Toán lớp 10 Học kì 2 năm 2023 (15 đề)

Haylamdo biên soạn và sưu tầm Bộ Đề thi Toán lớp 10 Học kì 2 năm 2023 (15 đề) được tổng hợp chọn lọc từ đề thi môn Toán 10 của các trường trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong các bài thi Toán lớp 10.

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 2

Năm học 2023 - 2022

Môn: Toán 10

Thời gian làm bài: 90 phút

(Đề số 1)

Giải phương trình, bất phương trình sau

Câu 1:

Câu 2:

Câu 3:

Câu 4:

Câu 5: Cho 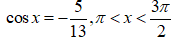. Tính giá trị biểu thức A = 2sinx + cos2x

Câu 6: Chứng minh rằng biểu thức 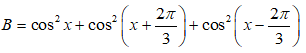không phụ thuộc vào biến x.

Câu 7: Chứng minh rằng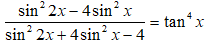

Câu 8: Phân tích thành tích biểu thức sau sin2x + cos2x + cosx - sinx

Câu 9: Tính giá trị biểu thức C = sin²50⁰ + sin²70⁰ + sin50⁰.sin70⁰

Câu 10: Cho tam giác nhọn ABC. Chứng minh rằng: cotA.cotB + cotB.cotC + cotC.cotA = 1.

Câu 11: Tìm các giá trị nguyên của tham số m sao cho phương trình (m + 1)x² - 2(m - 1)x + 3m - 3 = 0 có hai nghiệm phân biệt.

Câu 12: Tìm điều kiện của tham số m để bất phương trình x² + (m - 2)x - 8m + 1 < 0 vô nghiệm.

• Giả thiết này dung chung cho các câu 13, 14, 15, 16, 17.

Trong mặt phẳng với hệ trục toạ độ Oxy, cho tam giác ABC biết phương trình đường thẳng lần lượt chứa các cạnh của tam giác là:

AB: 4x + 7y - 1 = 0; BC: 4x + 3y - 5 = 0; AC: y = 3

Câu 13: Tìm toạ độ trọng tâm G của tam giác.

Câu 14: Viết phương trình đường cao AK của tam giác.

Câu 15: Tính cosB, S_ΔABC.

Câu 16: Viết phương trình đường phân giác trong của góc C.

Câu 17: Viết phương trình đường tròn ngoại tiếp tam giác ABC.

Giả thiết này dung chung cho các câu 18, 19.

Trong mặt phẳng với hệ trục toạ độ Oxy, cho đường tròn (C): x² + y² - 4x - 2y - 20 = 0

Câu 18: Xác định toạ độ tâm và bán kính của đường tròn (C).

Câu 19: Viết phương trình tiếp tuyến của đường tròn (C) biết tiếp tuyến song song với đường thẳng Δ: 4x + 3y - 10 = 0.

Câu 20: Trong mặt phẳng Oxy, viết phương trình đường thẳng d đi qua M(2;1) và cắt đường tròn (C): x² + y² + 2x - 4y - 4 = 0 theo một dây cung AB có độ dài bằng 4.

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 2

Năm học 2023 - 2022

Môn: Toán 10

Thời gian làm bài: 90 phút

(Đề số 2)

A. PHẦN TRẮC NGHIỆM (2 điểm) Chọn đáp án đúng trong mỗi câu sau:

Câu 1 (TH). Tập nghiệm của bất phương trình -x² + x + 12 ≥ 0 là:

A. (-∞;-3]∪[4;+∞).

B. ∅.

C. (-∞;-4]∪[3;+∞).

D. [-3;4].

Câu 2 (TH). Tập nghiệm của bất phương trình 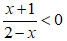là:

A. [-1;2].

B. (-1;2).

C. (-∞;-1)∪(2;+∞).

D. [-1;2).

Câu 3 (VD). Có bao nhiêu giá trị nguyên của tham số m để với mọi x∈R, biểu thức f(x) = x² + (m + 2)x + 8m + 1 luôn nhận giá trị dương?

A. 27

B. 28

C. Vô số

D. 26

Câu 4 (NB). Cho bảng số liệu thống kê điểm kiểm tra 1 tiết môn Toán của 40 học sinh như sau:

Điểm	3	4	5	6	7	8	9	10	Cộng
Số học sinh	2	3	7	18	3	2	4	1	40

Số trung vị (M_e) và mốt M_o của bảng số liệu thống kê trên là:

A. M_e = 8; M_o = 40.

B. M_e = 6; M_o = 18.

C. M_e = 6,5; M_o = 6.

D. M_e = 7; M_o = 6.

Câu 5 (TH). Biểu thức P = sin(π + x) - 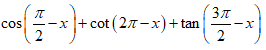có biểu thức rút gọn là:

A. P = 2sinx

B. P = -2sinx

C. P = 0

D. P = -2cotx

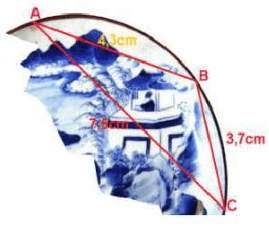
Câu 6 (VD). Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (AB = 4,3cm; BC = 3,7cm; CA = 7,5cm). Bán kính của chiếc đĩa này bằng (kết quả làm tròn tới hai chữ số sau dấu phẩy)

A. 5,73 cm

B. 6,01 cm

C. 5,85 cm

D. 4,57 cm

Câu 7 (TH). Phương trình tham số của đường thẳng đi qua 2 điểm A(3;-1), B(-6;2) là:

Câu 8 (TH). Tìm tất cả các giá trị của tham số m để phương trình x² + y² - 2(m + 2)x + 4my + 19m - 6 = 0 là phương trình đường tròn.

A. 1 < m < 2

B. m < -2 hoặc m > -1

C. m < -2 hoặc m > 1

D. m < 1 hoặc m > 2

II. PHẦN TỰ LUẬN (8 điểm)

Câu 1 (VD) (2,5 điểm). Giải các bất phương trình sau

Câu 2 (VD) (1,5 điểm).

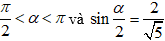
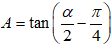
Cho góc α thỏa mãn . Tính giá trị của biểu thức .

Câu 3 (VD) (3,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho điểm A(3;1), đường thẳng Δ: 3x + 4y + 1 và đường tròn (C): x² + y² - 2x - 4y + 3 = 0:

a) Tìm tọa độ tâm, tính bán kính của đường tròn (C). Viết phương trình tiếp tuyến của đường tròn (C) biết tiếp tuyến đó song song với đường thẳng Δ.

b) Viết phương trình tổng quát của đường thẳng d đi qua điểm A và cắt đường tròn (C) tại hai điểm B, C sao cho BC = .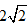

c) Tìm tọa độ điểm M(x₀; y₀) nằm trên đường tròn (C) sao cho biểu thức T = x₀ + y₀ đạt giá trị lớn nhất, giá trị nhỏ nhất.

Câu 4 (VDC) (1,0 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0;2].