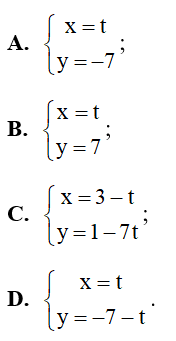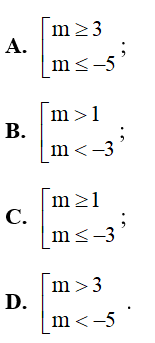Đề thi Học kì 2 Toán lớp 10 năm 2023 có đáp án (4 đề - Sách mới)

---

Đề thi Học kì 2 Toán lớp 10 năm 2023 có đáp án (4 đề - Sách mới)

Haylamdo biên soạn và sưu tầm Đề thi Học kì 2 Toán lớp 10 sách mới năm 2023 có đáp án Kết nối tri thức, Cánh diều, Chân trời sáng tạo được tổng hợp chọn lọc từ đề thi môn Toán 10 của các trường trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong các bài thi Toán lớp 10.

Đề thi Học kì 2 Toán lớp 10 năm 2023 có đáp án (4 đề - Sách mới)

Xem thử Đề Toán 10 Cuối kì 2 KNTT Xem thử Đề Toán 10 Cuối kì 2 Cánh diều Xem thử Đề Toán 10 Cuối kì 2 CTST

Chỉ 100k mua trọn bộ Đề thi Toán 10 Cuối kì 2 (mỗi bộ sách) bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

• Đề thi Học kì 2 Toán lớp 10 Kết nối tri thức có đáp án (4 đề)

  Xem đề thi

• Đề thi Học kì 2 Toán lớp 10 Cánh diều có đáp án (4 đề)

  Xem đề thi

• Đề thi Học kì 2 Toán lớp 10 Chân trời sáng tạo có đáp án (4 đề)

  Xem đề thi

ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 NĂM HỌC 2023 (2 ĐỀ CÓ MA TRẬN + ĐÁP ÁN)

BỘ SÁCH: KẾT NỐI TRI THỨC VỚI CUỘC SỐNG

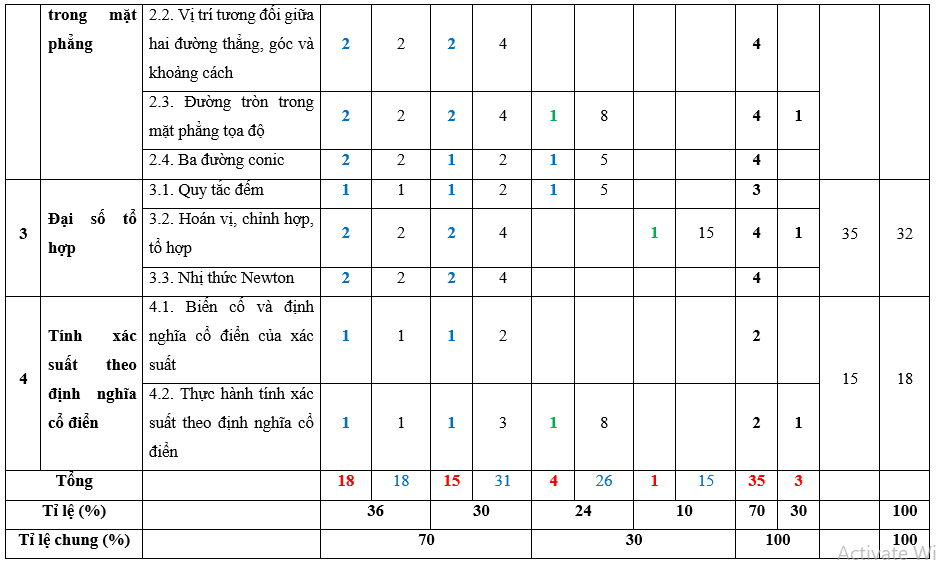
A. Ma trận đề thi

MÔN: TOÁN, LỚP 10 – THỜI GIAN LÀM BÀI: 90 phút

Câu hỏi trắc nghiệm: 35 câu (70%)

Câu hỏi tự luận : 3 câu (30%)

Lưu ý:

- Các câu hỏi ở cấp độ nhận biết, thông hiểu, vận dụng là các câu hỏi trắc nghiệm khách quan 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.

- Các câu hỏi ở cấp độ vận dụng và vận dụng cao tô màu xanh lá là các câu hỏi tự luận.

- Số điểm tính cho 1 câu trắc nghiệm là 0,2 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ điểm được quy định trong ma trận.

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Kết nối tri thức

Năm học 2023

Môn: Toán lớp 10

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 1)

I. TRẮC NGHIỆM (7 ĐIỂM)

Câu 1. Cho hàm số dưới dạng bảng như sau:

x	1	2	3	4	5
y	0	1	2	3	4

Giá trị của hàm số y tại x = 3 là

A. 2;

B. 3;

C. 4;

D. 5.

Câu 2. Trục đối xứng của hàm số bậc hai y = 3t² – 6.

A. t = 0;

B. t = – 1;

C. t = 1;

D. t = 2.

Câu 3. Cho hàm số bậc hai y = 2x² + 3x – 8. Hoành độ đỉnh của đồ thị hàm số bậc hai này là

A. $-\frac{3}{4}$;

B. $\frac{3}{4}$;

C. $\frac{3}{2}$;

D. $-\frac{3}{2}$.

Câu 4. Cho parabol y = ax² + bx – 3. Xác định hệ số a, b biết parabol có đỉnh

I(– 1; – 5)

A. a = 1; b = 2;

B. a = 1; b = – 2;

C. a = – 2; b = 4;

D. a = 2; b = 4.

Câu 5. Hàm số bậc hai y = ax² + bx + c (a ≠ 0) luôn dương khi

A. a > 0, ∆ > 0;

B. a < 0, ∆ < 0;

C. a > 0, ∆ < 0;

D. a < 0, ∆ > 0.

Câu 6. Tập ngiệm của bất phương trình: x(x + 5) ≤ 2(x² + 2) là:

A. $(–\infty ;1]\cup [4;+\infty )$ ;

B. $\left[1;4\right]$ ;

C. $(–\infty ;1)\cup (4;+\infty )$;

D. (1; 4).

Câu 7. Nghiệm của phương trình $\sqrt{8-x^2}=\sqrt{x+2}$ là

A. x = – 3;

B. x = – 2;

C. x = 2;

D. $\left[\begin{array}{l}x=2\\ x=-3\end{array}\right.$.

Câu 8. Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Oy?

A. $\overrightarrow{u_1}=\left(1;-1\right);$

B. $\overrightarrow{u_2}=\left(0;1\right);$

C. $\overrightarrow{u_3}=\left(1;0\right);$

D. $\overrightarrow{u_4}=\left(1;1\right).$

Câu 9. Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng $d:\left\{\begin{array}{l}x=2\\ y=-1+6t\end{array}\right.$?

A.$\overrightarrow{u_1}=\left(6;0\right)$;

B.$\overrightarrow{u_2}=\left(-6;0\right)$;

C.$\overrightarrow{u_3}=\left(2;6\right)$;

D.$\overrightarrow{u_4}=\left(0;1\right)$.

Câu 10. Cho α là góc tạo bởi hai đường thẳng d₁: a₁x + b₁y + c₁ = 0 và d₂: a₂x + b₂y + c₂ = 0. Khẳng định nào sau đây là đúng?

A. cosα = $\frac{a_1{a}_2+b_1{b}_2}{\sqrt{{a_1}^2+{b_1}^2}.\sqrt{{a_2}^2+{b_2}^2}}$;

B. cosα = $\frac{\left|a_1{b}_1+a_2{b}_2\right|}{({a_1}^2+{b_1}^2).({a_2}^2+{b_2}^2)}$;

C. cosα =$\frac{\left|a_1{b}_1-a_2{b}_2\right|}{\sqrt{{a_1}^2+{b_1}^2}.\sqrt{{a_2}^2+{b_2}^2}}$;

D. cosα = $\frac{\left|a_1{a}_2+b_1{b}_2\right|}{\sqrt{{a_1}^2+{b_1}^2}.\sqrt{{a_2}^2+{b_2}^2}}$.

Câu 11. Góc tạo bởi hai đường thẳng d₁: 2x – y – 10 = 0 và d₂: x − 3y + 9 = 0

A. 30^°;

B. 45^°;

C. 60^°;

D. 135^°.

Câu 12. Cho 4 điểm A(4; – 3) ; B(5; 1), C(2; 3) và D(– 2; 2). Xác định vị trí tương đối của hai đường thẳng AB và CD:

A. Trùng nhau;

B. Song song;

C. Vuông góc ;

D. Cắt nhau nhưng không vuông góc

Câu 13. Phương trình x² + y² – 2ax – 2by + c = 0 là phương trình đường tròn (C) khi và chỉ khi

A. a² + b² > 0;

B. a² + b² − c = 0;

C. a² + b² − c < 0;

D. a² + b² − c > 0.

Câu 14. Đường tròn (C): x² + y² – 6x + 2y + 6 = 0 có tâm I và bán kính R lần lượt là:

A. I(3; −1) và R = 4;

B. I(3; 1) và R = 4;

C. I(3; −1) và R = 2;

D. I(-6; 2) và R = 2.

Câu 15. Cho đường tròn (C) có đường kính AB với A(−2; 1), B(4; 1). Khi đó, phương trình đường tròn (C):

A. x² + y² + 2x + 2y + 9 = 0;

B. x² + y² + 2x + 2y – 7 = 0;

C. x² + y² – 2x – 2y – 7 = 0;

D. x² + y² – 2x – 2y + 9 = 0.

Câu 16. Cho phương trình x² + y² – 2mx – 4(m – 2)y + 6 – m = 0 (1) . Tìm điều kiện của m để (1) là phương trình đường tròn.

A. m ∈ (1; 2);

B. m ∈ (−∞; 1) ∪ (2; +∞);

C. m ∈ (−∞; 1] ∪ [2; +∞);

D. m ∈ [1; 2].

Câu 17. Hai tiêu điểm của hypebol $\frac{x^2}{16}-\frac{y^2}{9}=1$

A. F₁ (−3; 0) và F₂ (3; 0);

B. F₁ (−4; 0) và F₂ (4; 0);

C. F₁ (−5; 0) và F₂ (5; 0);

D. F₁ (−6; 0) và F₂ (6; 0).

Câu 18. Cho phương trình $y=\frac{x^2}{a^2}+\frac{y^2}{b^2}$ là phương trình của elip khi

A. a > b > 0;

B. a, b > 0;

C. a = b > 0;

D. Với mọi giá trị của a và b.

Câu 19. Phương trình chính tắc của elip có độ dài tiêu cự bằng 6 và tổng khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm bằng 8 là:

A. 16x² + 7y² = 112;

B. $\frac{x^2}{64}+\frac{y^2}{28}=1$;

C. 7x² + 16y² = 1;

D. $\frac{x^2}{16}+\frac{y^2}{7}=1$.

Câu 20. Cho parabol (P): y² = 4x và 2 điểm A(0; -4) , B(-6; 4).Tìm điểm C thuộc (P) sao cho tam giác ABC vuông tại A

A. C(16; 8) hoặc $\left(\frac{16}{9};\frac{-8}{3}\right)$;

B. C(16; 8);

C. C$\left(\frac{16}{9};\frac{8}{3}\right)$;

D. C(16; -8) hoặc C$\left(\frac{16}{9};\frac{8}{3}\right)$.

Câu 21. Giả sử một công việc có thể thực hiện theo một trong hai phương án khác nhau:

- Phương án 1 có n₁ cách thực hiện;

- Phương án 2 có n₂ cách thực hiện (không trùng với bất kì phương án thực hiện nào của cách số 1)

Vậy số cách thực hiện công việc có:

A. n₁ + n₂ (cách thực hiện);

B. n₁ . n₂ (cách thực hiện);

C. ${\left(n_1\right)}^{n_2}$(cách thực hiện);

D. n₂ – n₁ (cách thực hiện).

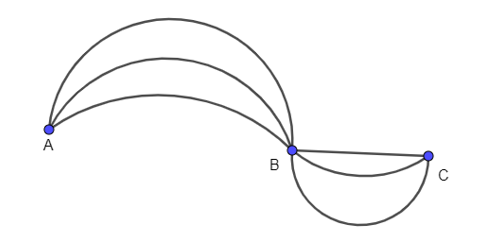
Câu 22. Bạn An muốn đi từ địa điểm A đến địa điểm C thì phải đi qua địa điểm B như sơ đồ dưới đây:

Có bao nhiêu cách để An đi từ địa điểm A đến địa điểm C?

A. 6; B. 3; C. 9; D. 5.

Câu 23. Có bao nhiêu số chẵn gồm 3 chữ số phân biệt nhỏ hơn 547?

A. 80;

B. 128;

C. 114;

D. 149.

Câu 24. Có hai kiểu mặt đồng hồ đeo tay (vuông, tròn) và có ba kiểu dây (kim loại, da, nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?

A. 7;

B. 6;

C. 8;

D. 5.

Câu 25. Công thức nào dưới đây là đúng?

A. $A_n^k=\frac{n!}{\left(n-k\right)!}\left(1\le k\le n\right)$;

B. $C_n^k=C_n^{n-k}\left(0\le k\le n\right)$;

C. $P_n=A_n^n\left(n>0,n\in \mathbb{N}\right)$;

D. Cả A, B, C đều đúng.

Câu 26. Cho tập hợp E gồm 10 phần tử. Hỏi có bao nhiêu tập con có 8 phần tử của tập hợp E?

A. 100;

B. 80;

C. 45;

D. 90.

Câu 27. Trong một kì thi THPT Quốc gia tại một điểm thi có 5 sinh viên tình nguyện được phân công trực hướng dẫn thí sinh thi ở 5 vị trí khác nhau. Yêu cầu mỗi vị trí có đúng 1 sinh viên. Hỏi có nhiêu cách phân công vị trí trực cho 5 người đó.

A. 120;

B. 625;

C. 3125;

D. 80.

Câu 28. Khai triển của (a + b)³ là

A. a³ + 3a²b + 3ab² + 1³;

B. (a – b)(a² + ab + b²);

C. a³ + 3a²b + 3ab² + b³;

D. (a + b)(a² – ab + b).

Câu 29. Cho khai triển (a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + ... ab⁴ + b⁵. Số cần điền vào chỗ ... là

A. 10;

B. 5;

C. – 5;

D. – 10.

Câu 30. Hệ số của x⁴ trong khai triển (3 – 4x)⁵ là

A. 1 024;

B. 4 320;

C. – 5 760;

D. 3 840

Câu 31. Khẳng định nào sau đây đúng về biến cố đối của biến cố E?

A. Biến cố đối của E được kí hiệu là – E;

B. Biến cố đối của E là phần bù của E trong $\Omega$;

C. A và B đều sai;

D. A và B đều đúng.

Câu 32. Xếp ngẫu nhiên 3 bạn An; Bình ; Cường đứng thành 1 hàng dọc. Tính xác suất để Bình và Cường đứng cạnh nhau.

A. $\frac{2}{3}$;

B. $\frac{5}{6}$;

C. $\frac{1}{3}$;

D. $\frac{1}{2}$.

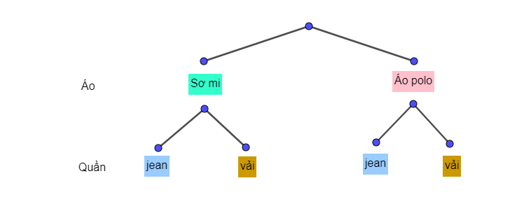
Câu 33. Sơ đồ cây dưới đây biểu diễn các lựa chọn trang phục đi học của bạn Linh.

Dựa vào sơ đồ cây cho biết bạn Linh có bao nhiêu sự lựa chọn trang phục tới trường?

A. 4;

B. 2;

C. 6;

D. 1.

Câu 34. Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của biến cố A :” 4 viên bi lấy ra có ít nhất một viên bi màu đỏ”

A. n(A) = 7366;

B. n(A) = 7563;

C. n(A) = 7566;

D. n(A) = 7568.

Câu 35. Cho đường thẳng $d:3x+5y+2022=0$. Hệ số góc của đường thẳng d là

A. (d) có hệ số góc $k=\frac{3}{5}$;

B. (d) có hệ số góc $k=-\frac{5}{3}$;

C. (d) có hệ số góc $k=-\frac{3}{5}$;

D. (d) có hệ số góc $k=\frac{5}{3}$.

II. PHẦN TỰ LUẬN (3 ĐIỂM)

Bài 1. (1 điểm) Trong một lớp có 18 học sinh nam và 12 học sinh nữ. Hỏi có bao nhiêu cách chọn 3 học sinh để

a) trong ba bạn có duy nhất một bạn nữ?

b) làm ban cán sự lớp gồm lớp trưởng, lớp phó học tập và lớp phó văn thể mĩ?

Bài 2. (1 điểm)

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có phương trình (x – 2)² + (y – 1)² = 10.

a) Lập phương trình tiếp tuyến với đường tròn (C) tại điểm M(5; 2).

b) Tìm điều kiện của m để đường thẳng (d_m): x – my – 4 = 0 cắt đường tròn (C) theo một dây cung có độ dài bằng 6.

Bài 3. (1 điểm) Đề thi trắc nghiệm môn Toán gồm 50 câu hỏi, mỗi câu có 4 phương án trả lời trong đó chỉ có một phương án trả lời đúng. Mỗi câu trả lời đúng được 0,2 điểm. Một học sinh không học bài nên mỗi câu trả lời đều chọn ngẫu nhiên một phương án. Xác suất để học sinh đó được đúng 6 điểm là bao nhiêu?

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Cánh diều

Năm học 2023

Môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 2)

I. PHẦN TRẮC NGHIỆM (7 điểm)

Câu 1. Một lớp có 31 học sinh nam và 16 học sinh nữ. Có bao nhiêu cách chọn một học sinh làm lớp trưởng của lớp.

A. 31;

B. 16;

C. 47;

D. 15.

Câu 2. Số cách sắp xếp 6 bạn học sinh thành một hàng dọc là:

A. 6 cách;

B. 12 cách;

C. 720 cách;

D. 18 cách.

Câu 3. Có bao nhiêu số tự nhiên có 5 chữ số, các chữ số khác 0 và đôi một khác nhau.

A. 5!;

B. 9⁵;

C. $A_9^5$;

D. 5⁹.

Câu 4. Khai triển biểu thức (a + 2b)⁵ ta thu được kết quả là:

A. a⁵ + 10a⁴b + 40a³b² + 80a²b³ + 80ab⁴ + 32b⁵;

B. a⁵ – 10a⁴b – 40a³b² – 80a²b³ – 80ab⁴ – 32b⁵;

C. a⁵ + 20a⁴b + 30a³b² + 80a²b³ + 80ab⁴ + 32b⁵;

D. a⁵ + 10a⁴b + 40a³b² + 60a²b³ + 60ab⁴ + 32b⁵.

Câu 5. Tổng các hệ số trong khai triển $P\left(x\right)={\left(1+x\right)}^5$ là:

A. 30;

B. 31;

C. 32;

D. 33.

Câu 6. Giá trị nào dưới đây là giá trị chính xác của số π ?

A. 3,14;

B. 3,1;

C. 3,146;

D. Không có câu trả lời đúng.

Câu 7. Quy tròn số 3,1234567 đến hàng phần nghìn. Số gần đúng nhận được là:

A. 3,124;

B. 3,123;

C. 3,12;

D. 3,1235.

Câu 8. Thực hiện đo chiều dài của bốn cây cầu, kết quả đo đạc nào trong các kết quả sau đây là chính xác nhất?

A. 15,34 m ± 0,01 m;

B. 127,4 m ± 0,2 m;

C. 2135,8 m ± 0,5 m;

D. 63,47 m ± 0,15 m.

Câu 9. Giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là

A. trung bình;

B. tứ phân vị;

C. trung vị;

D. mốt.

Câu 10. Cho mẫu số liệu sau: 11; 16; 17; 19; 20; 21; 22; 23; 23; 24; 25. Trung vị của mẫu số liệu là

A. 21;

B. 20,5;

C. 21,5;

D. 22.

Câu 11. Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau:

So sánh Q₃ và Q₁ ?

A. Q₃ > Q₁;

B. Q₃ < Q₁;

C. Q₁ = Q₃;

D. Q₃ = 3Q₁.

Câu 12. Điểm thi học kì I môn Toán của lớp 10A được thống kê trong bảng sau:

Điểm trung bình môn Toán của lớp 10A₂ là

A. 4;

B. 5,5;

C. 5,45;

D. 6.

Câu 13. Chọn khẳng định đúng: “Trong một mẫu số liệu, khoảng biến thiên là…”

A. hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó;

B. tổng số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó;

C. tích giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó;

D. thương giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó.

Câu 14. Sản lượng lúa (đơn vị là tạ) của 40 thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng số liệu sau:

Phương sai của bảng số liệu trên là:

A. 1,52;

B. 1,53;

C. 1,54;

D. 1,55.

Câu 15. Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau:

Khoảng tứ phân vị của bảng số liệu trên là:

A. 30;

B. 10;

C. 20;

D. 5.

Câu 16. Gieo một đồng xu ba lần liên tiếp. Xác suất để ba lần tung kết quả giống nhau là:

A. 0,25;

B. 0,5;

C. 1;

D. 0,75.

Câu 17. Một túi chứa 2 viên bi màu trắng và 3 viên bi màu đen. Lấy ngẫu nhiên 3 viên bi. Xác suất để lấy được ít nhất 1 bi trắng là:

A. 0,9;

B. 0,8;

C. 0,1;

D. 0,2.

Câu 18. Xác suất của biến cố A, kí hiệu là:

A. P(A);

B. n(A);

C. C(A);

D. Ω(A).

Câu 19. Trong mặt phẳng tọa độ Oxy, cho G(3; 5). Tọa độ của $\overrightarrow{OG}$ là

A. (3; –5);

B. (5; 3);

C. (–3; –5);

D. (3; 5).

Câu 20. Trong mặt phẳng tọa độ Oxy, cho hai điểm $M\left(x_M;y_M\right)$ và $N\left(x_N;y_N\right)$. Khi đó ta có tọa độ $\overrightarrow{MN}$ là:

A. $\overrightarrow{MN}=\left(x_N+x_M;y_N+y_M\right)$;

B. $\overrightarrow{MN}=\left(x_M-x_N;y_N-y_M\right)$;

C. $\overrightarrow{MN}=\left(x_M-x_N;y_M-y_N\right)$;

D.$\overrightarrow{MN}=\left(x_N-x_M;y_N-y_M\right)$.

Câu 21. Trong mặt phẳng tọa độ Oxy, cho hai điểm B(–1; 3) và C(5; 2). Tọa độ của $\overrightarrow{BC}$ là:

A.$\overrightarrow{BC}=\left(6;-1\right)$;

B.$\overrightarrow{BC}=\left(-6;1\right)$;

C.$\overrightarrow{BC}=\left(4;5\right)$;

D. $\overrightarrow{BC}=\left(-6;-1\right)$.

Câu 22. Trong mặt phẳng tọa độ Oxy, cho $\overrightarrow{a}=\left(a_1;a_2\right),\overrightarrow{b}=\left(b_1;b_2\right)$ và $\overrightarrow{x}=\left(a_1+b_1;a_2+b_2\right)$. Khi đó $\overrightarrow{x}$ bằng:

A.$\overrightarrow{a}.\overrightarrow{b}$;

B.$\overrightarrow{a}+\overrightarrow{b}$;

C.$\overrightarrow{a}-\overrightarrow{b}$;

D.$k\overrightarrow{a}\left(k\in ℝ\right)$.

Câu 23. Trong mặt phẳng tọa độ Oxy, cho$\overrightarrow{u}=\left(3;-6\right)$. Khi đó $\frac{1}{2}\overrightarrow{u}$ là:

A. $\frac{1}{2}\overrightarrow{u}=\left(6;-12\right)$;

B. $\frac{1}{2}\overrightarrow{u}=\left(\frac{5}{2};-\frac{13}{2}\right)$;

C. $\frac{1}{2}\overrightarrow{u}=\left(\frac{7}{2};-\frac{11}{2}\right)$;

D. $\frac{1}{2}\overrightarrow{u}=\left(\frac{3}{2};-3\right)$.

Câu 24. Cho đường thẳng d có phương trình:$\left\{\begin{array}{l}x=2+3t\\ y=-3-t\end{array}\right.$ . Một vectơ chỉ phương của d có tọa độ là:

A. (2; –3);

B. (3; –1);

C. (3; 1);

D. (3; –3).

Câu 25. Cho đường thẳng ∆: x – 3y – 2 = 0. Tọa độ của vectơ nào sau đây không phải là vectơ pháp tuyến của ∆?

A.${\overrightarrow{n}}_1=\left(1;-3\right)$;

B.${\overrightarrow{n}}_2=\left(-2;6\right)$;

C.${\overrightarrow{n}}_3=\left(\frac{1}{3};-1\right)$;

D.${\overrightarrow{n}}_4=\left(3;1\right)$.

Câu 26. Cho tam giác ABC có tọa độ 3 đỉnh A(4; 5), B(–6; –1), C(1; 1). Phương trình đường cao BH của tam giác ABC là:

A. 3x – 4y – 14 = 0;

B. 3x + 4y – 22 = 0;

C. 3x + 4y + 22 = 0;

D. 3x – 4y + 14 = 0.

Câu 27. Cho tam giác ABC có tọa độ đỉnh B(4; –3). Đường trung tuyến AM có phương trình $\left\{\begin{array}{l}x=1+3t\\ y=-2-7t\end{array}\right.$. Đường cao AH có phương trình 2x + 5y + 66 = 0. Khi đó phương trình đường trung trực của cạnh AB có phương trình là:

A. 13x – 3y + 100 = 0;

B. 3x – 13y – 140 = 0;

C. 3x – 13y + 140 = 0;

D. 13x + 3y – 100 = 0.

Câu 28. Cho đường thẳng d₁, d₂ có vectơ pháp tuyến lần lượt là ${\overrightarrow{n}}_1=\left(a;b\right),{\overrightarrow{n}}_2=\left(c;d\right)$. Kết luận nào sau đây đúng?

A. $\cos \left(d_1,d_2\right)=\frac{\left|ab+cd\right|}{\sqrt{a^2+c^2}.\sqrt{b^2+d^2}}$;

B. $\cos \left(d_1,d_2\right)=\frac{\left|ac+bd\right|}{\sqrt{a^2+c^2}.\sqrt{b^2+d^2}}$;

C.$\cos \left(d_1,d_2\right)=\frac{\left|ac+bd\right|}{\sqrt{a^2+b^2}.\sqrt{c^2+d^2}}$;

D.$\cos \left(d_1,d_2\right)=\frac{ac+bd}{\sqrt{a^2+b^2}.\sqrt{c^2+d^2}}$.

Câu 29. Vị trí tương đối của hai đường thẳng$d_1:\frac{x}{2}-\frac{y}{3}=1$ và d₂: 6x – 4y – 8 = 0 là:

A. Song song;

B. Trùng nhau;

C. Cắt nhau nhưng không vuông góc với nhau;

D. Vuông góc với nhau.

Câu 30. Tâm của đường tròn (C) có phương trình: (x – 2)² + (y + 5)² = 12 là:

A. D(2; 5);

B. E(5; 2);

C. F(2; –5);

D. G(–2; 5).

Câu 31. Đường tròn tâm I(1; 4) và đi qua điểm B(2; 6) có phương trình là:

A. (x + 1)² + (y + 4)² = 5;

B.${\left(x-1\right)}^2+{\left(y-4\right)}^2=\sqrt{5}$;

C.${\left(x+1\right)}^2+{\left(y+4\right)}^2=\sqrt{5}$;

D. (x – 1)² + (y – 4)² = 5.

Câu 32. Cho đường tròn (C): (x – 2)² + (y – 2)² = 9. Phương trình tiếp tuyến của (C) đi qua điểm A(5; –1) là:

A. x + y – 4 = 0 hoặc x – y – 2 = 0;

B. x = 5 hoặc y = –1;

C. 2x – y – 3 = 0 hoặc 3x + 2y – 2 = 0;

D. 3x – 2y – 2 = 0 hoặc 2x + 3y + 5 = 0.

Câu 33. Cho hai điểm F₁, F₂ cố định có khoảng cách F₁F₂ = 2c (c > 0) và một số a < c và a > 0. Tập hợp các điểm M sao cho |MF₁ – MF₂| = 2a được gọi là:

A. Đường hypebol;

B. Đường elip;

C. Đường parabol;

D. Đường tròn.

Câu 34. Điểm nào là tiêu điểm của parabol y² = 5x?

A. F(5; 0);

B. $F\left(\frac{5}{2};0\right)$;

C.$F\left(\pm \frac{5}{4};0\right)$;

D.$F\left(\frac{5}{4};0\right)$.

Câu 35. Cho elip (E): 9x² + 36y² – 144 = 0. Tỉ số$\frac{c}{a}$bằng:

A.$\frac{\sqrt{3}}{2}$;

B.$\frac{2\sqrt{3}}{3}$;

C.$\sqrt{3}$;

D.$\frac{\sqrt{3}}{3}$.

II. PHẦN TỰ LUẬN (3 điểm)

Câu 1. (1,0 điểm)

Một bàn dài có hai dãy ghế ngồi đối diện nhau, mỗi dãy gồm 4 ghế. Người ta xếp chỗ ngồi cho 4 học sinh trường A và 4 học sinh trường B vào bàn nói trên. Hỏi xác suất xếp các học sinh vào hai dãy ghế sao cho bất cứ hai học sinh nào ngồi đối diện nhau khác trường với nhau?

Câu 2. (1,0 điểm)

Sản lượng lúa (tạ) của 40 thửa ruộng thí nghiệm (cho giống lúa mới) có cùng diện tích được trình bày trong bảng phân bố tần số sau đây:

Sản lượng	20	21	22	23	24
Tần số	5	8	11	10	6

Hỏi sản lượng lúa trung bình thu được là bao nhiêu tạ? Tìm khoảng tứ phân vị của dãy số liệu trên.

Câu 3. (1,0 điểm)

Trong mặt phẳng Oxy, cho đường tròn (C): x² + y² – 2x + 2y – 2 = 0.

a) Viết phương trình đường thẳng (∆) song song với (d): 4x – 3y + 3 = 0 và tiếp xúc với (C).

b) Viết phương trình đường thẳng (d) qua A(3; 2) và tiếp xúc với (C).

c) Tìm điểm M thuộc (d’): x – 2y – 1 = 0 sao cho từ M vẽ được hai tiếp tuyến đến (C) vuông góc với nhau.

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Chân trời sáng tạo

Năm học 2023

Môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 3)

Câu 1. Cho bảng biến thiên:

Bảng biến thiên đã cho là bảng biến thiên của hàm số nào sau đây?

A. $f\left(x\right)=-x^2-3x+10$ ;

B. $f\left(x\right)=x^2-3x-10$ ;

C. $f\left(x\right)=x^2+3x-10$ ;

D. $f\left(x\right)=-x^2+3x+10$ .

Câu 2. Tọa độ tiêu điểm của parabol (P): y² = x là

A. $F\left(\frac{1}{2};0\right)$ ;

B. $F_1\left(-\frac{1}{2};0\right)$ và $F_2\left(\frac{1}{2};0\right)$;

C. $F\left(\frac{1}{4};0\right)$ ;

D. $F_1\left(-\frac{1}{4};0\right)$ và $F_2\left(\frac{1}{4};0\right)$.

Câu 3. Nếu tam thức bậc hai $f\left(x\right)=-x^2+ax+b$ có $\Delta \le 0$ thì

A. $f\left(x\right)\ge 0\forall x\in ℝ$ ;

B. $f\left(x\right)>0\forall x\in ℝ$ ;

C. $f\left(x\right)<0\forall x\in ℝ$ ;

D. $f\left(x\right)\le 0\forall x\in ℝ$ .

Câu 4. Bất phương trình nào sau đây là bất phương trình bậc hai một ẩn?

A. $\sqrt{x+1}\le 2$ ;

B. $\left(x+2\right)\left(3-x\right)<0$ ;

C. $x^3+2x-3>0$ ;

D. $4-5x\ge 0$ .

Câu 5. Viết phương trình tham số của đường thẳng qua hai điểm $A\left(3;-7\right)$ và $B\left(1;-7\right)$ .

Câu 6. Trong mặt phẳng Oxy ,đường tròn $\left(C\right):{\left(x-2\right)}^2+{\left(y+3\right)}^2=9$ có tâm I và bán kính R là:

A. $I\left(-3;2\right)$ , $R=3$ ;

B. $I\left(2;-3\right)$ , $R=3$ ;

C. $I\left(-2;3\right)$ , $R=3$ ;

D. $I\left(2;3\right)$ , $R=9$ .

Câu 7. Khoảng cách từ điểm $M(1;-1)$ đến đường thẳng $\Delta :3x-4y-17=0$ là:

A. $\frac{10}{\sqrt{5}}$ ;

B. 2;

C. $\frac{2}{5}$ ;

D. $\frac{18}{5}$ .

Câu 8. Elip $\frac{x^{\text{2}}}{\text{5}}\text{+}\frac{y^{\text{2}}}{\text{4}}=1$ có tiêu cự bằng

A. 9;

B. 4;

C. 2 ;

D. 1.

Câu 9. Tập nghiệm của bất phương trình $x^2+2x-15>0$ là

A. $\left(-\infty ;-5\right)\cup \left(3;+\infty \right)$ ;

B. $\left(-\infty ;-3\right)\cup \left(5;+\infty \right)$ ;

C. $\left(-5;3\right)$ ;

D. $\left(-3;5\right)$ .

Câu 10.Cho đường thẳng $d:3x-7y+15=0$ . Mệnh đề nào sau đây sai?

A. d đi qua 2 điểm $M\left(-\frac{1}{3};2\right)$ và $N\left(5;0\right)$;

B. d có hệ số góc $k=\frac{3}{7}$ ;

C. d không đi qua gốc toạ độ;

D. $\overrightarrow{u}=\left(7;3\right)$ là vectơ chỉ phương của d .

Câu 11. Phương trình đường thẳng đi qua $N(1;2)$và song song với đường thẳng $2x+3y-12=0$ là

A. $2x-3y-8=0$ ;

B. $2x+3y+8=0$ ;

C. $2x+3y-8=0$ ;

D. $4x+6y+1=0$ .

Câu 12. Tính góc tạo bởi giữa hai đường thẳng $d_1:2x-y-10=0$ và $d_2:x-3y+9=0.$

A. ${135}^{\text{o}}$ ;

B. ${45}^{\text{o}}$;

C. ${30}^{\text{o}}$ ;

D. 60°.

Câu 13. Tìm tất cả các giá trị của m để phương trình $x^2-2\left(m+1\right)x+4=0$ có nghiệm.

Câu 14. Đường tròn (C) có tâm $I(-1;3)$ và tiếp xúc với đường thẳng $d:3x-4y+5=0$ có phương trình là

A. ${(x+1)}^2+{(y-3)}^2=2$ ;

B. ${(x+1)}^2-{(y-3)}^2=10$ ;

C. ${(x+1)}^2+{(y-3)}^2=4$ ;

D. ${(x-1)}^2+{(y+3)}^2=2$ .

Câu 15. Viết phương trình chính tắc của elip, biết elip có tiêu cự bằng 2 và độ dài trục lớn bằng 10.

A. $\frac{x^{\text{2}}}{\text{25}}-\frac{y^{\text{2}}}{\text{16}}=1$ ;

B. $\frac{x^{\text{2}}}{\text{25}}\text{+}\frac{y^{\text{2}}}{\text{9}}=1$ ;

C. $\frac{x^{\text{2}}}{\text{25}}\text{+}\frac{y^{\text{2}}}{\text{24}}=1$ ;

D. $\frac{{\text{x}}^{\text{2}}}{\text{100}}\text{+}\frac{{\text{y}}^{\text{2}}}{\text{81}}$ = 1.

Câu 16. Trong mặt phẳng tọa độ Oxy cho $\Delta :x-y+1=0$ và hai điểm $A(2;1)$ ,$B(9;6)$ . Điểm nằm trên đường $\Delta$ sao cho $MA+MB$ nhỏ nhất. Tính a +b ta được kết quả là:

A. 9;

B. - 7;

C. -9 ;

D. 7.

Câu 17. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn $\left(C\right):x^2+y^2-2x-4y+3=0$ . Viết phương trình tiếp tuyến của đường tròn biết tiếp tuyến đó song song với đường thẳng $\Delta :3x+4y+1=0$ .

A. $3x+4y-5\sqrt{2}+11=0$ , $3x+4y-5\sqrt{2}-11=0$ ;

B. $3x+4y+5\sqrt{2}-11=0$ , $3x+4y-5\sqrt{2}-11=0$ ;

C. $3x+4y+5\sqrt{2}-11=0$ , $3x+4y+5\sqrt{2}+11=0$ ;

D. $3x+4y+5\sqrt{2}-11=0$ ; $3x+4y-5\sqrt{2}+11=0$ .

Câu 18. Tính tổng tất cả các nghiệm nguyên của bất phương trình $\sqrt{14+5x-x^2}=x+1$ .

A. 5;

B. 0;

C. 3;

D. 6.

Câu 19. Có bao nhiêu giá trị nguyên của m để biểu thức $f\left(x\right)=\left(m+2\right)x^2+2\left(m+2\right)x-m-7$ luôn âm?

A. 4;

B. 1;

C. 2;

D. 3.

Câu 20. Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có diện tích bằng 12 và tâm I là giao điểm của hai đường thẳng $d_1:x-y-3=0,d_2:x+y-6=0$; trung điểm cạnh AD là giao điểm của $d_1$ và Ox. Biết đỉnh $A\left(a;b\right)$ và có tung độ dương. Tính $a^2+2b$.

A. 18;

B. 14;

C. 11;

D. 6.

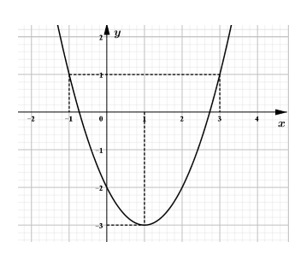
Câu 21. Cho parabol $y=f\left(x\right)$ có đồ thị như hình vẽ sau.

Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số $g\left(x\right)=f\left(\frac{1}{2}\cos 4x-4{\sin }^{2}x+\frac{5}{2}\right)$ . Tính $M-2m$ .

A. 3.

B. 5.

C. 7.

D. 1.

Câu 22. Với n là số nguyên dương tùy ý, mệnh đề nào dưới đây đúng ?

A. ${\text{C}}_n^1=1$;

B. ${\text{C}}_n^n=2n$;

C. ${\text{C}}_n^{n-1}={\text{C}}_n^1$;

D. ${\text{C}}_n^0=n$.

Câu 24.Có bao nhiêu cách chọn 4 học sinh từ một nhóm có 10 học sinh ?

A. ${\text{C}}_6^4$;

B. ${\text{A}}_{10}^4$;

C. ${10}^4$;

D. $C_{10}^4$.

Câu 25. ${\text{P}}_4$ bằng

A. 16;

B. 4;

C. 24;

D. 40.

Câu 26.Có bao nhiêu cách chọn ra một bông hoa từ 6 bông hoa hồng khác nhau và 4 bông hoa cúc khác nhau?

A. 10;

B. $6!.4!$;

C. 10!;

D. 1.

Câu 27.Có bao nhiêu cách chọn ra 2 học sinh có cả nam và nữ từ một nhóm học sinh gồm 6 nam và 4 nữ ?

A. 21;

B. 10;

C. 45;

D. 24.

Câu 28. Không gian mẫu của phép thử gieo một đồng xu hai lần có bao nhiêu phần tử ?

A. 8;

B. 4;

C. 2;

D. 6.

Câu 29. Cho tập hợp $A=\text{{}1;2;3;4;5;6\}$ , chọn ngẫu nhiên một phần tử từ tập hợp A. Tính xác suất để chọn được phần tử là số lẻ.

A.1;

B.0;

C. $\frac{1}{2}$ ;

D. $\frac{3}{4}$ .

Câu 30. Cho $n\in \mathbb{N},n\ge 3$ và ${\text{C}}_n^3=2n$ . Giá trị của n bằng

A. 8 ;

B. 6 ;

C. 4;

D. 5.

Câu 31. Hệ số của $x^3$ trong khai triển ${\left(x+2\right)}^5$ bằng

A.10;

B. 60;

C. 80;

D. 40.

Câu 32. Số hạng $x^{3}y$ trong khai triển ${\left(2x+y\right)}^4$ bằng

A.32;

B. 8x³y;

C. 32x³y;

D. 24x³y.

Câu 33. Gieo một con súc sắc 6 mặt, cân đối và đồng chất một lần. Xác suất để xuất hiện mặt có số chấm nhỏ hơn 5 bằng

A. $\frac{1}{3}$ ;

B. $\frac{1}{6}$ ;

C. $\frac{2}{3}$ ;

D. $\frac{1}{2}$ .

Câu 34. Một hộp chứa 10 thẻ được ghi số từ 1 đến 10 Chọn ngẫu nhiên một thẻ, xác suất để chọn được thẻ ghi số lớn hơn 8 bằng

A. $\frac{1}{2}$ ;

B. $\frac{1}{5}$ ;

C. $\frac{1}{10}$ ;

D. 1.

Câu 35. Một hộp chứa 6 viên bi đỏ và 4 viên bi xanh. Lấy ngẫu nhiên đồng thời 2 viên bi, xác suất để lấy được 2 viên bi màu xanh bằng

A. $\frac{2}{15}$ ;

B. $\frac{1}{9}$ ;

C. $\frac{7}{15}$ ;

D. $\frac{2}{5}$ .

II. PHẦN TỰ LUẬN (3 điểm)

Câu 1. (1,5 điểm):

a) Tìm số hạng không chứa x của khai triển: ${\left(x+\frac{2}{x}\right)}^5$ .

b) Một tổ có 9 học sinh gồm 5 học sinh nam và 4 học sinh nữ, trong đó có 2 học sinh nam tên Phúc và Đức. Xếp ngẫu nhiên 9 học sinh trên thành một hàng ngang. Có bao nhiêu cách xếp sao cho hai học sinh Phúc và Đức luôn đứng cạnh nhau, đồng thời các học sinh nam còn lại không đứng cạnh nhau và cũng không đứng cạnh Phúc và Đức.

Câu 2. (1,5 điểm):

a) Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 1)² + (y + 2)² = 34 và đường thẳng d: 3x + 5y + 23 = 0. Viết phương trình tiếp tuyến của đường tròn (C) biết tiếp tuyến đó vuông góc với đường thẳng d.

b) Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; 18), B(1; 7), C(– 2; 3). Tìm tọa độ điểm M nằm trên đường thẳng BC sao cho độ dài đoạn AM là ngắn nhất.

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Năm học 2023

Môn: Ngữ Văn 10

Thời gian làm bài: 90 phút

(Đề số 4)

Phần I: Trắc nghiệm

Câu 1: VTCP của đường thẳng là:

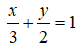
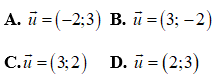
Câu 2: Cho . Khẳng định nào sau đây đúng?

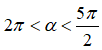
A. cot⁡α > 0     B. cot⁡α < 0.

C. cot⁡α < 0.     D. cot⁡α > 0.

Câu 3: Vectơ pháp tuyến của đường thẳng đi qua hai điểm A(2;3) và B(4;1) là:

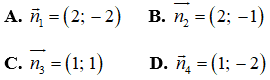
Câu 4: Tập nghiệm của hệ bất phương trình là:

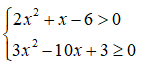
A. S = (-∞;-2]    B. S = (3;+∞)

C. S = (-2;3)     D. S = (-∞;-2]∪(3;+∞)

Câu 5: Cho góc α thỏa mãn . Tính tan⁡α.

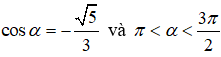
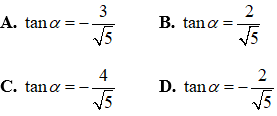
Câu 6: Giá trị của m để bất phương trình m²x + m(x + 1) - 2(x - 1) > 0 nghiệm đúng với mọi x ∈ [-2;1] là:

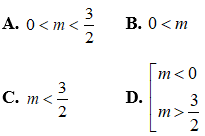
Câu 7: Phương trình đường thẳng Δ đi qua điểm M(2;-5) và có hệ số góc k = -2 là:

A. y = -2x - 1     B. y = -2x - 9

C. y = 2x - 1     D. y = 2x - 9

Câu 8: Trong mặt phẳng với hệ trục tọa độ Oxy, cho elip (E) có độ dài trục lớn bằng 12 và độ dài trục bé bằng 6. Phương trình nào sau đây là phương trình của elip (E).

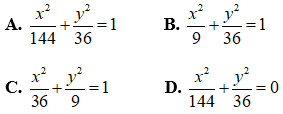
Câu 9: Cho hai điểm A(1;2) và B(4;6). Tọa độ điểm M trên trục Oy sao cho diện tích tam giác MAB bằng 1 là:

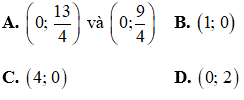
Câu 10: Trong mặt phẳng tọa độ Oxy, đường tròn (C) tâm I(-3;4), bán kính R = 6 có phương trình là:

A. (x + 3)² + (y - 4)² = 36     B. (x - 3)² + (y + 4)² = 6

C. (x + 3)² + (y - 4)² = 6     D. (x - 3)² + (y + 4)² = 36

Phần II: Tự luận

Câu 1: Giải các bất phương trình sau:

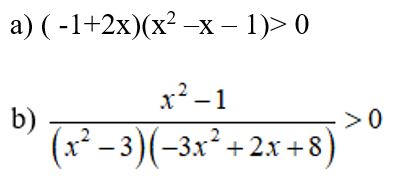
Câu 2: Tìm tất cả các giá trị của tham số m để hệ bất phương trình sau có nghiệm.

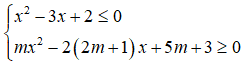
Câu 3: Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào x.

A = 2(sin⁴x + cos⁴x + sin²x.cos²x)² - (sin⁸x + cos⁸x)

Câu 4: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2;4), trọng tâm . Biết rằng đỉnh B nằm trên đường thẳng d: x + y + 2 = 0 và đỉnh C có hình chiếu vuông góc trên d là điểm H(2;-4). Giả sử B(a;b). Tính giá trị của biểu thức P = a - 3b.

Đáp án & Hướng dẫn giải

Phần I: Trắc nghiệm

Câu hỏi	1	2	3	4	5
Đáp án	B	A	C	D	B
Câu hỏi	6	7	8	9	10
Đáp án	A	B	C	A	A

Câu 1: Chọn B.

Ta có:

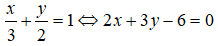
⇒ Đường thẳng có VTPT là . Suy ra VTCP là

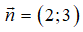
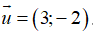
Câu 2: Chọn A.

Ta có:

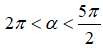
⇒ Điểm cuối cùng α - π thuộc góc phần tư thứ I

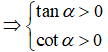
Câu 3: Chọn C.

Ta có: A(2;3), B(4;1)

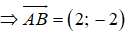
⇒ VTPT đi qua hai điểm A(2;3) và B(4;1) là

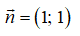
Câu 4: Chọn D.

Ta có

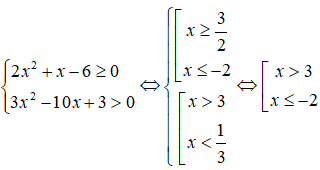
Vậy tập nghiệm hệ bất phương trình là S = (-∞;-2] ∪ (3;+∞).

Câu 5: Chọn B.

Ta có :

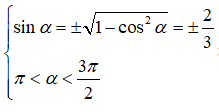
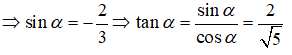
Câu 6: Chọn A.

Đặt: f(x) = (m² + m – 2)x + m + 2

Bài toán thỏa mãn:

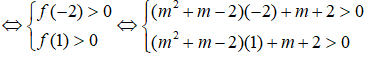
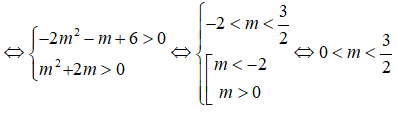
Câu 7: Chọn B.

Phương trình đường thẳng Δđi qua điểm M(2;-5) và có hệ số góc k = -2 là:

y = -2(x - 2) - 5 ⇔ y = -2x - 1

Câu 8: Chọn C.

Phương trình chính tắc của elip có dạng (E):

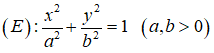
Ta có a = 6, b = 3, vậy phương trình của Elip là:

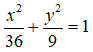
Câu 9: Chọn A.

Hai điểm A(1;2) và B(4;6) ⇒ AB = 5

Gọi M(0;m).

Vì diện tích tam giác MAB bằng 1

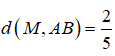
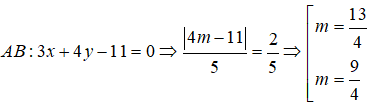
Câu 10: Chọn A.

Phương trình đường tròn (C) tâm I(-3;4), bán kính R = 6 là:

[x - (-3)]² + (y - 4)² = 6² ⇒ (x + 3)² + (y - 4)² = 36

Phần II: Tự luận

Câu 1:

a) Bảng xét dấu

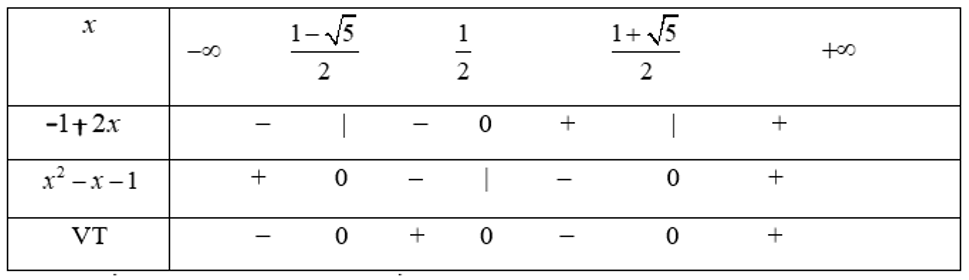
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là:

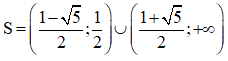
b) Bảng xét dấu

Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là:

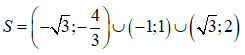
Câu 2:

Ta có bất phương trình x² - 3x + 2 ≤ 0 ⇔ 1 ≤ x ≤ 2.

Yêu cầu bài toán tương đương với bất phương trình:

mx² – 2(2m + 1)x + 5m + 3 ≤ 0 (1) có nghiệm x ∈ S = [1;2].

Ta đi giải bài toán phủ định là: Tìm m để bất phương trình (1) vô nghiệm trên S

Tức là bất phương trình f(x) = mx² - 2(2m + 1)x + 5m + 3 < 0 (2) đúng với mọi x ∈ S.

• m = 0 ta có (2) -2x + 3 < 0 ⇔ x > 3/2 nên (2) không đúng với ∀x ∈ S

• m ≠ 0 tam thức f(x) có hệ số a = m, biệt thức Δ' = -m² + m + 1

Bảng xét dấu

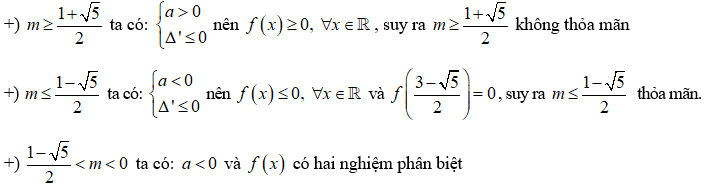
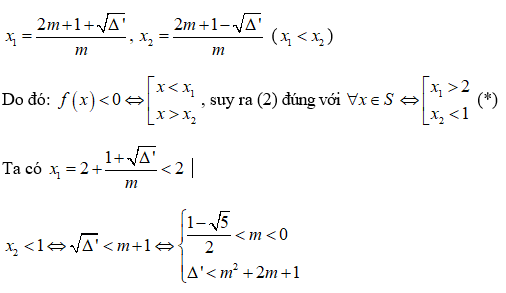
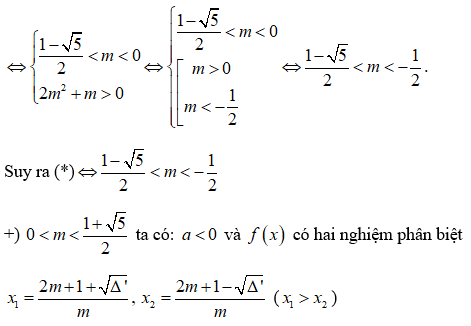
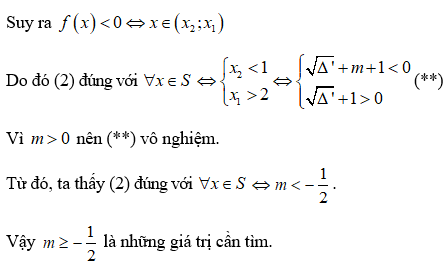
Câu 3:

Ta có:

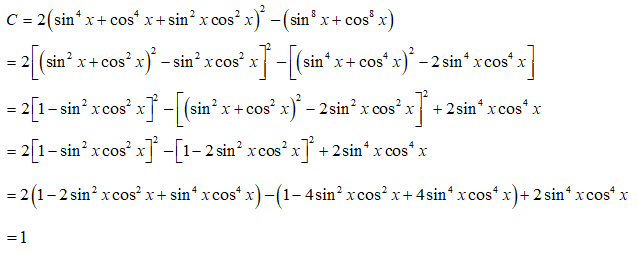
Vậy giá trị của biểu thức không phụ thuộc vào x.

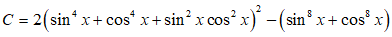
Câu 4:

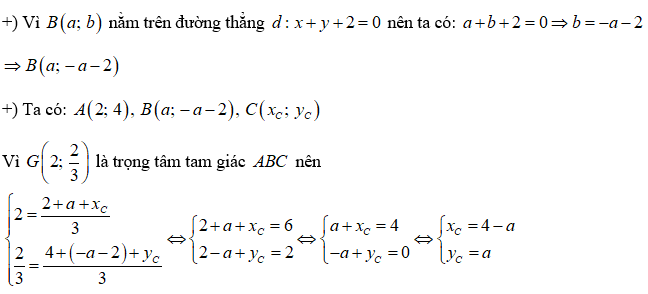
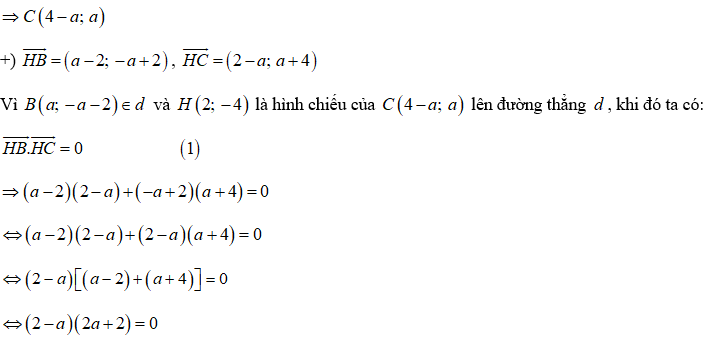
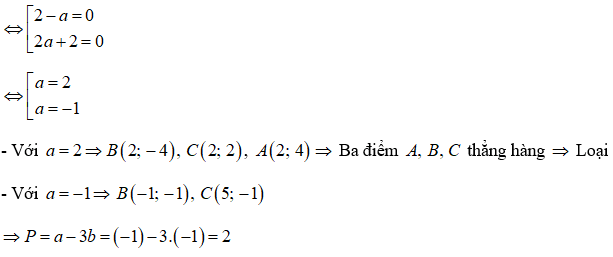
Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Năm học 2023

Môn: Ngữ Văn 10

Thời gian làm bài: 90 phút

(Đề số 5)

Phần I: Trắc nghiệm

Câu 1: Cho . Kết quả đúng là:

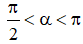
A. sin⁡α > 0, cos⁡α < 0     B. sin⁡α > 0, cos⁡α < 0

C. sin⁡α > 0, cos⁡α < 0     D. sin⁡α > 0, cos⁡α < 0

Câu 2: Tọa độ tâm I của đường tròn (C): x² + y² - 6x - 8y = 0 là

A. I(-3;-4)     B. I(3;4)

C. I(-6;-8)     D. I(6;8)

Câu 3: Số nghiệm nguyên của bất phương trình là

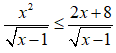
A. 3     B. 4

C. 5     D. 6

Câu 4: Trong mặt phẳng với hệ trục tọa độ Oxy, cho elip (E) có độ dài trục lớn bằng 10 và độ dài tiêu cự bằng 6. Phương trình nào sau đây là phương trình của elip (E).

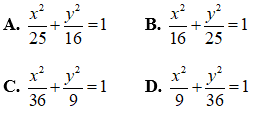
Câu 5: Độ dài của cung có số đo π/2 rad, trên đường tròn bán kính r=20 là:

Câu 6: Giá trị của là

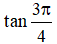
A. 1     B. √2

C. -1     D. 0

Câu 7: Cho hai điểm A(-3;6) và B(1;3). Phương trình đường trung trực của AB là:

A. 3x + 4y - 15 = 0     B. 4x - 3y + 30 = 0

C. 8x - 6y + 35 = 0     D. 3x - 4y + 21 = 0

Câu 8: Trong các phương trình sau, phương trình nào là phương trình đường tròn?

A. 4x² + y² - 10x + 4y - 2 = 0

B. x² + y² - 4x - 8y + 1 = 0

C. x² + 2y² - 4x + 6y - 1 = 0

D. x² + y² - 2x - 8y + 30 = 0

Câu 9: Tam thức bậc hai f(x) = x² - 12x - 13 nhận giá trị không âm khi và chỉ khi:

A. x ∈ (-1;13)     B. x ∈ R\[-1;13]

C. x ∈ [-1;13]     D. x ∈ (-∞;-1] ∪ [13;+∞)

Câu 10: Điều kiện của bất phương trình là:

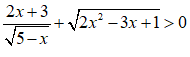
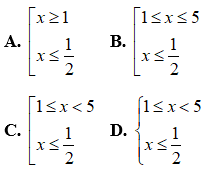
Câu 11: Giải hệ bất phương trình

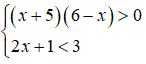
A. -5 < x < 1     B. x > -5

C. x < -5     D. x < 1

Câu 12: VTCP của đường thẳng là:

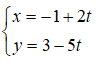
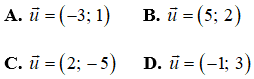
Câu 13: Cho góc α thỏa mãn và sin⁡α + 2cos⁡α = -1. Giá trị sin⁡2α là:

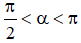
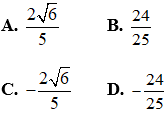
Câu 14: Đường thẳng Δ: 3x-2y-7=0 cắt đường thẳng nào sau đây?

A. d₁: 3x + 2y = 0     B. d₂: 3x - 2y = 0

C. d₃: -3x + 2y - 7 = 0     D. d₄: 6x - 4y - 14 = 0

Câu 15: Góc tạo bởi hai đường thẳng d₁: x - y - 2 = 0 và d₂: 2x + 3y + 3 = 0 là:

A. 11^o 19'     B. 78^o 41'

C. 79^o 41'     D. 10^o 19'

Câu 16: Cho đường thẳng d: x - 2y - 3 = 0. Tọa độ hình chiếu vuông góc H của điểm M(0;1) trên đường d là:

A. H(-1;2)     B. H(5;1)

C. H(3;0)     D. H(1;-1)

Câu 17: Cho đường tròn (C): (x - 1)² + (y + 3)² = 10 và đường thẳng Δ: x + y + 1 = 0, biết đường tròn (C) cắt Δ tại hai điểm phân biệt A và B. Độ dài đoạn thẳng AB bằng:

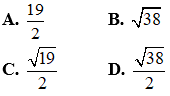
Câu 18: Giá trị của m để phương trình (m - 1)x² - (2m - 2)x + 2m = 0 vô nghiệm là:

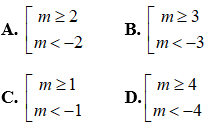
Câu 19: Cho tam giác ABC có A(-2;0), B(0;3), C(3;1). Đường thẳng đi qua B và song song với AC có phương trình:

A. 5x - y + 3 = 0     B. 5x + y - 3 = 0

C. x + 5y - 15 = 0     D. x - 5y + 15 = 0

Câu 20: Tập nghiệm của bất phương trình là:

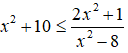
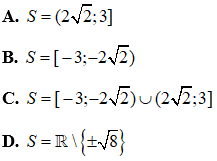
Phần II: Tự luận

Câu 1: Giải các bất phương trình và hệ bất phương trình:

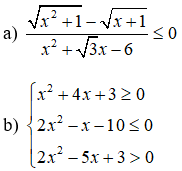
Câu 2:

a) Cho . Tính giá trị của biểu thức

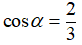
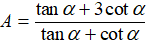
b) Cho

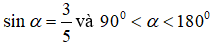
Tính giá trị của biểu thức:

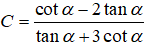
Câu 3: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC cân tại B với A(1;-1), C(3;5). Điểm B nằm trên đường thẳng d: 2x - y = 0. Phương trình các đường thẳng AB, BC lần lượt là ax + by - 24 = 0, cx + dy + 8 = 0. Tính giá trị biểu thức a.b.c.d.

Đáp án & Hướng dẫn giải

Phần I: Trắc nghiệm

Câu hỏi	1	2	3	4	5
Đáp án	C	B	A	A	D
Câu hỏi	6	7	8	9	10
Đáp án	C	C	B	D	C
Câu hỏi	11	12	13	14	15
Đáp án	A	C	D	A	B
Câu hỏi	16	17	18	19	20
Đáp án	D	B	C	D	C

Câu 1: Chọn C.

Ta có:

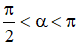
⇒ Điểm cuối của góc α thuộc góc phần tư thứ hai của đường tròn lượng giác .

⇒ sin⁡α > 0, cos⁡ α < 0

Câu 2: Chọn B.

(C): x² + y² - 6x - 8y = 0

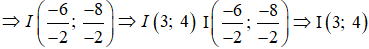
Câu 3: Chọn A.

Điều kiện: x > 1

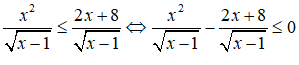
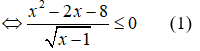
Vì với ∀x > 1 nên bất phương trình (1) tương đường với x² - 2x - 8 ≤ 0 ⇔ -2 ≤ x ≤ 4.

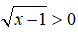
Kết hợp với điều kiện x > 1 suy ra 1 ≤ x ≤ 4 ⇒ x ∈ {2;3;4}

Vậy bất phương trình có ba nghiệm nguyên.

Câu 4: Chọn A.

Độ dài trục lớn bằng 10 ⇒ 2a = 10 ⇔ a = 5, a² = 25

Độ dài tiêu cự bằng 6 ⇒ 2c = 6 ⇔ c = 3

Ta có: a² - b² = c² ⇒ b² = a² - c² = 5² - 3² = 16

Vậy phương trình của elip (E) là:

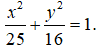
Câu 5: Chọn D.

Ta có:

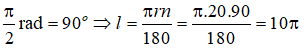
Vậy l = 10π.

Câu 6: Chọn C.

Ta có:

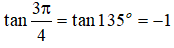
Câu 7: Chọn C.

+ Gọi I là trung điểm của AB

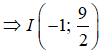
+ A(-3;6),B(1;3)

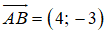
+ Phương trình đường trung trực của AB đi qua

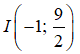
và nhận là VTPT:

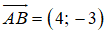
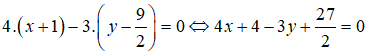
⇔ 8x + 8 - 6y + 27 = 0 ⇔ 8x - 6y + 35 = 0

Câu 8: Chọn B.

Phương trình đường tròn có hệ số của x² và y² bằng nhau ⇒ Loại đáp án A và C

Xét đáp án B: x² + y² - 4x - 8y + 1 = 0 ⇒ a = 2, b = 4, c = 1 ⇒ a² + b² - c > 0 ⇒ Nhận

Xét đáp án C: x² + y² - 2x - 8y + 30 = 0 ⇒ a = 1, b = 4, c = 30 ⇒ a² + b² - c < 0 ⇒ Loại

Câu 9: Chọn D.

Tam thức bậc hai f(x) = x² - 12x - 13 nhận giá trị không âm khi và chỉ khi

f(x) ≥ 0 ⇔ x² - 12x - 13 ≥ 0

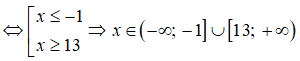
Câu 10: Chọn C.

Điều kiện xác định của bất phương trình là:

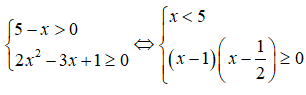
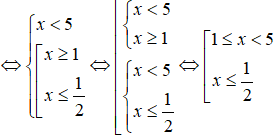
Câu 11: Chọn A.

Xét hệ bất phương trình:

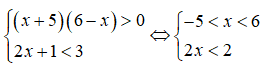
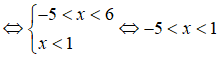
Câu 12: Chọn C.

VTCP của đường thẳng

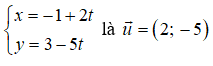
Câu 13: Chọn D.

Vì ⇒ sin⁡α > 0, cos⁡α < 0.

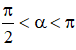
Từ sin⁡α + 2cos⁡α = -1 ⇒ sin⁡α = -1 - 2cos⁡α.

Ta có:

(-1 - 2cos⁡α)² + cos²⁡ α = 1

⇔ 1 + 4cos⁡α + 4cos²⁡α + cos²⁡α = 1

⇔ 5cos²⁡α + 4cos⁡α = 0

⇔ cos⁡α.(5cos⁡α + 4) = 0

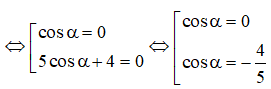
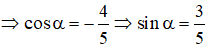
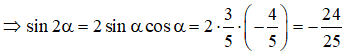
Câu 14: Chọn A.

Xét đường thẳng Δ: 3x - 2y - 7 = 0 và d₁: 3x + 2y = 0 ta có:

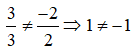
Câu 15: Chọn B.

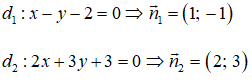
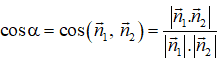
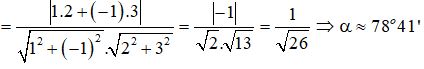
Câu 16: Chọn D.

Gọi Δ là đường thẳng đi qua M và vuông góc với đường thẳng d.

d: x - 2y - 3 = 0

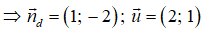
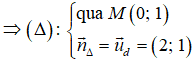
⇒ 2.(x - 0) + 1.(y - 1) = 0 ⇔ 2x + y - 1 = 0

Gọi H = d ∩ (Δ). Tọa độ điểm H là nghiệm của hệ phương trình:

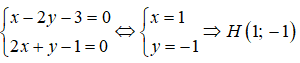
Câu 17: Chọn B.

Vì đường tròn (C) cắt Δ tại hai điểm phân biệt A và B nên tọa độ điểm A và B là nghiệm của hệ phương trình:

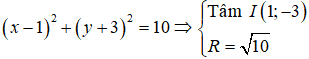
Gọi H là trung điểm của AB suy ra IH ⊥ AB ⇒ IH ⊥ Δ.

Xét tam giác AIH vuông tại H ta có:

AH² + IH² = AI² ⇒ AH² = AI² - IH²

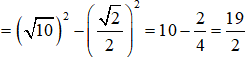
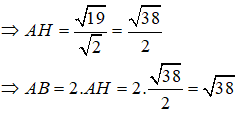
Câu 18: Chọn C.

Với m = 1 thỏa mãn yêu cầu bài toán

Với m ≠ 1 phương trình vô nghiệm khi và chỉ khi Δ' < 0

⇔ (m - 1)² - 2m(m - 1) < 0 ⇔ (m - 1)(-m - 1) < 0

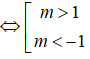
Vậy với thì phương trình có nghiệm

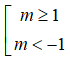
Câu 19: Chọn D.

Gọi (d) là đường thẳng cần tìm. Do (d) song song với AC nên nhận làm VTCP.

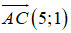
Suy ra là VTPT của (d).

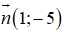
⇒ (d) có phương trình: 1(x - 0) - 5(y - 3) = 0 ⇔ x - 5y + 15 = 0

Câu 20: Chọn C.

Ta có

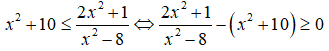
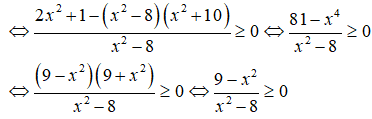
Bảng xét dấu

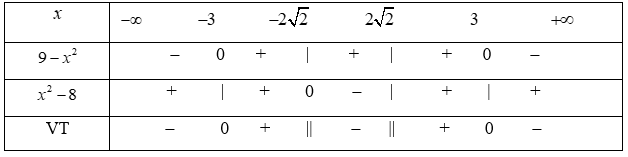
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là S = [-3;-2√2) ∪ (2√2;3].

Phần II: Tự luận

Câu 1:

a) ĐKXĐ:

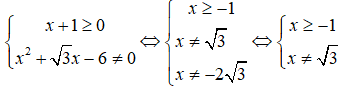
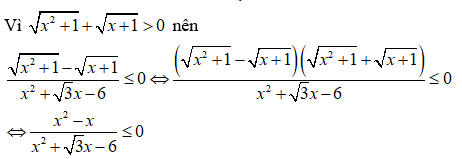
Bảng xét dấu

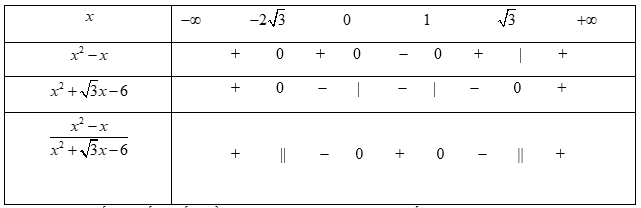
Dựa vào bảng xét dấu và đối chiếu điều kiện, ta có tập nghiệm của bất phương trình đã cho là S = [-1;0]∪[1;√3)

b) Ta có:

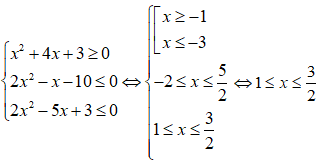
Vậy tập nghiệm hệ bất phương trình là

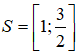
Câu 2:

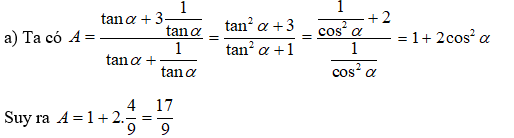
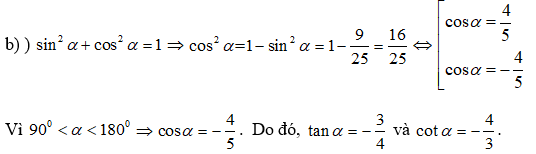
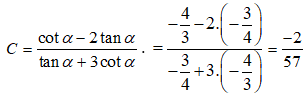
Câu 3:

Giả sử I(x_I;y_I) là trung điểm của AC

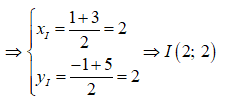
Vì tam giác ABC cân tại B nên BI ⊥ AC. Phương trình đường thẳng BI đi qua I(2;2) nhận làm VTPT là:

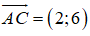
2.(x - 2) + 6.(y - 2) = 0 ⇔ 2x - 4 + 6y - 12 = 0 ⇔ 2x + 6y - 16 = 0 ⇔ x + 3y - 8 = 0

Tọa độ giao điểm B của BI và d là nghiệm của hệ phương trình:

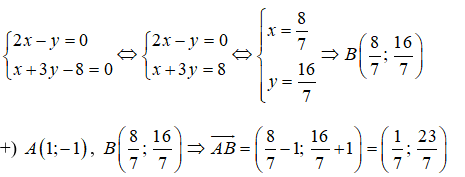
Phương trình đường thẳng AB đi qua A(1;-1) nhận làm VTPT là:

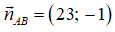
23.(x - 1) - 1.(y + 1) = 0 ⇔ 23x - 23 - y - 1 = 0 ⇔ 23x - y - 24 = 0

⇒ a = 23; b = -1

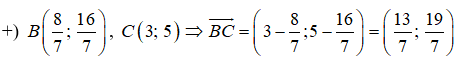
Phương trình đường thẳng BC đi qua C(3;5) nhận làm VTPT là:

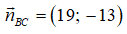
19.(x - 3) + (-13).(y - 5) = 0 ⇔ 19x - 57 - 13y + 65 = 0 ⇔ 19x - 13y + 8 = 0

⇒ c = 19; d = -13

⇒ a.b.c.d = 23.(-1).19.(-13) = 5681

Vậy a.b.c.d = 5681.

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Năm học 2023

Môn: Ngữ Văn 10

Thời gian làm bài: 90 phút

(Đề số 6)

Phần I: Trắc nghiệm

Câu 1: Đường tròn (C): x² + y² - 2x + 4y - 3 = 0 có tâm I, bán kính R là:

A. I(-1;2), R = √2     B. I(-1;2), R = 2√2

C. I(1;-2), R = √2     D. I(1;-2), R = 2√2

Câu 2: Tìm các giá trị của tham số m để x² - 2x - m ≥ 0 ∀x

A. m ≤ 0     B. m < 0

C. m ≤ -1     D. m < -1

Câu 3: Hình vuông ABCD có A(2;1), C(4;3). Tọa độ của đỉnh B có thể là:

A. (-2;-3)     B. (1;4)

C. (-4;-1)     D. (-3;-2)

Câu 4: Cho đường thẳng Δ: x - 2y + 3 = 0. Vecto nào sau đây không là vecto chỉ phương của Δ?

A. (4;-2)     B. (-2;-1)

C. (2;1)     D. (4;2)

Câu 5: Tìm m để phương trình (m-1)x² - 2mx + 3m - 2 = 0 có hai nghiệm dương phân biệt?

A. m < 0,1 < m < 2     B. 1 < m < 2

C. m > 2     D. m < 1/2

Câu 6: Cho Elip (E): 4x² + 5y² = 20. Diện tích hình chữ nhật cơ sở của E là:

A. 2√5     B. 80

C. 8√5     D.40

Câu 7: Cho . Giá trị của là:

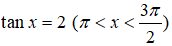
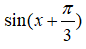
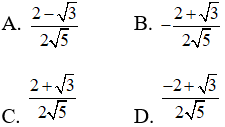
Câu 8: Tam giác ABC có A(1;2), B(0;4), C(3;1). Góc ∠BAC của tam giác ABC là:

A. 90^o     B. 36^o 52'

C. 143^o 7'     D. 53^o 7'

Câu 9: Tập nghiệm của hệ bất phương trình là:

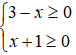
A. R     B. [-1;3]

C. ∅     D. (-1;3]

Câu 10: Bất phương trình có tập nghiệm là:

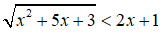
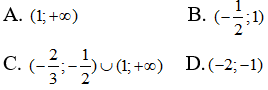
Câu 11: Với giá trị nào của m thì hai đường thẳng d: 2x + (m²+1)y - 3 = 0 và d': x + my - 10 = 0 song song?

A. m = 1 hoặc m = 2    B. m = 1 hoặc m = 0

C. m = 2     D. m = 1

Câu 12: Cho elip (E) đi qua điểm A(-3;0) và có tâm sai e = 5/6. Tiêu cự của (E) là:

A. 10     B. 5/3

C. 5     D. 10/3

Câu 13: Đẳng thức nào không đúng với mọi x?

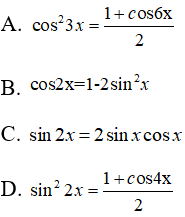
Câu 14: Cho đường tròn (C): x² + y² - 2x - 4y - 4 = 0. Phương trình tiếp tuyến của đường tròn tại điểm A(1;-1) là:

A. x + 1 = 0     B. y + 1 = 0

C. x + y + 1 = 0     D. x - y + 1 =0

Câu 15: Cho . Giá trị của tan⁡2x là:

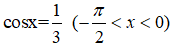
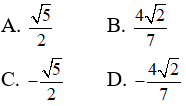
Câu 16: Rút gọn biểu thức sau ta được biểu thức nào sau đây?

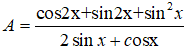
A. cosx     B. s⁡inx

C. tanx     D. cotx

Câu 17: Tập nghiệm của bất phương trình |x² - 1| > 2x - 1 là:

A. (0;2)     B. (-1-√3;-1+√√)

C.(-∞;-1+√√) ∪ (2;+∞)     D. (-∞;0) ∪ (2;+∞)

Câu 18: Trong mặt phẳng Oxy, khoảng cách từ điểm M(3;-4) đến đường thẳng d: 3x - 4y - 1 = 0 là:

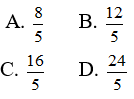
Câu 19: Giá trị nhỏ nhất của sin⁶⁡ x + cos⁶x là:

Câu 20: Phương trình tham số của đường thẳng đi qua A(2;7) có vecto chỉ phương là:

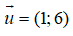
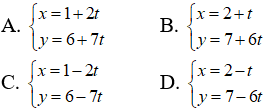
Phần II: Tự luận

Câu 1:

a) Giải bất phương trình và hệ bất phương trình sau:

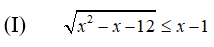
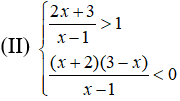
b) Tìm các giá trị của m để hàm số có tập xác định D = R

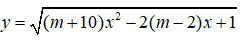
Câu 2: Tam giác ABC có . Chứng minh tam giác ABC vuông

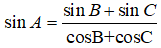
Câu 3: Trong mặt phẳng tọa độ cho hai điểm A(3;0), B(0;2) và đường thẳng d: x + y = 0.

a) Lập phương trình tham số của đường thẳng Δ đi qua A và song song với d

b) Lập phương trình đường tròn đi qua A,B và có tâm thuộc đường thẳng d

c) Lập phương trình chính tắc của elip đi qua điểm B và có tâm sai

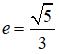
Đáp án & Hướng dẫn giải

Phần I: Trắc nghiệm

Câu hỏi	1	2	3	4	5
Đáp án	D	D	B	A	B
Câu hỏi	6	7	8	9	10
Đáp án	C	B	C	B	A
Câu hỏi	11	12	13	14	15
Đáp án	D	C	D	B	B
Câu hỏi	16	17	18	19	20
Đáp án	A	C	D	C	B

Câu 1: Đáp án: D

(C): x² + y² - 2x + 4y - 3 = 0 ⇔ (x - 1)² + (y + 2)² = 8

Suy ra, I(1;-2), R = √8 = 2√2

Câu 2: Đáp án: D

x² - 2x - m ≥ 0

Ta có: Δ' = (-1)² -1.(-m) = m + 1

Để x² - 2x - m ≥ 0 ∀x thì Δ' < 0 ⇔ m + 1 < 0 ⇔ m < -1

Câu 3: Đáp án: B

A(2;1), C(4;3) ⇒

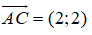
Gọi I là trung điểm của của AC ⇒ I(3;2)

Đường chéo BD là đường thẳng đi qua I và có vecto pháp tuyến là

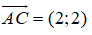
BD: 2(x - 3) + 2(y - 2) = 0 ⇔ x + y - 5 = 0

Thay tọa độ các điểm vào đường thẳng BD ta thấy tọa độ điểm ở đáp án B thỏa mãn phương trình đường thẳng BD.

Câu 4: Đáp án: A

Δ: x - 2y + 3 = 0 có

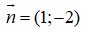
Ta thấy: (4;-2).(1;-2) = 4.1 + (-2).(-2) = 4 + 4 = 8 ≠ 0

Nên (4;-2) không phải là vecto chỉ phương của Δ

Câu 5: Đáp án: B

(m - 1)x² - 2mx + 3m - 2 = 0 (*)

Để phương trình (*) có hai nghiệm dương phân biệt thì:

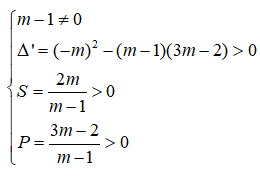
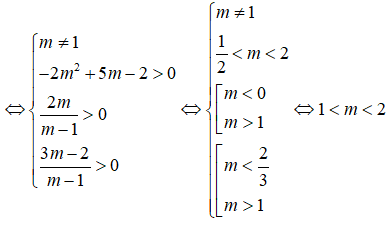
Câu 6: Đáp án: C

(E): 4x² + 5y² = 20

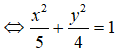
Ta có: a² = 5 ⇒ a = √5, b² = 4 ⇒ b = 2

Hình chữ nhật cơ sở có độ dài hai cạnh lần lượt là 2a = 2√5, 2b = 4

Suy ra, diện tích hình chữ nhật cơ sở là: 2√5.4 = 8√5

Câu 7: Đáp án: B

Ta có:

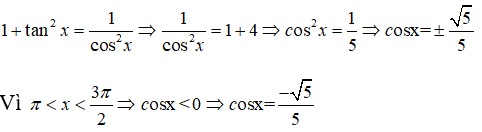
Mặt khác,

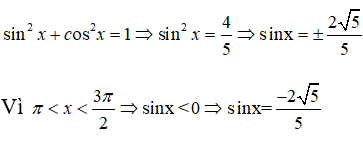
Ta có:

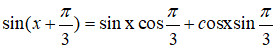
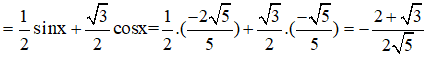
Câu 8: Đáp án: C

Ta có: A(1;2), B(0;4), C(3;1)

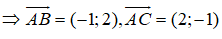
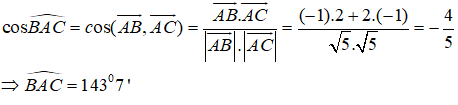
Câu 9: Đáp án: B

Ta có:

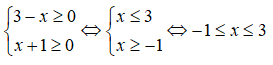
Vậy tập nghiệm của hệ bất phương trình là: [-1;3]

Câu 10: Đáp án: A

Ta có:

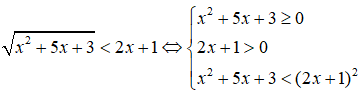
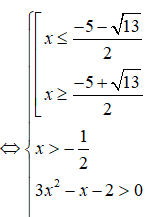
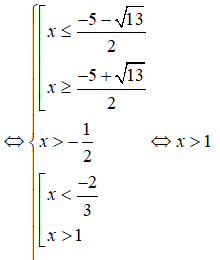
Câu 11: Đáp án: D

Để hai đường thẳng d: 2x + (m² + 1)y - 3 = 0 và d': x + my - 10 = 0 song song thì:

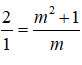
⇒ 2m = m² + 1 ⇔ m² - 2m + 1 = 0 ⇔ (m - 1)² = 0 ⇔ m = 1

Vậy với m = 1 thì d và d’ song song với nhau.

Câu 12: Đáp án: C

Cho elip (E) đi qua điểm A(-3;0) và có tâm sai

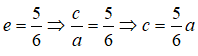
Giả sử elip có dạng:

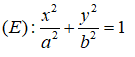
Vì (E) đi qua điểm

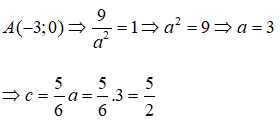
Vậy elip (E) có tiêu cự là:

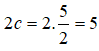
Câu 13: Đáp án: D

Áp dụng công thức hạ bậc ta có:

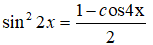
Vậy đáp án D sai

Câu 14: Đáp án: B

(C): x² + y² - 2x - 4y - 4 = 0 ⇔ (x - 1)² + (y - 2)² = 9

Đường tròn (C) có tâm I(1;2)

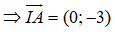
Tiếp tuyến của đường tròn tại A là đường thẳng đi qua A và nhận IA làm vecto pháp tuyến: -3(y + 1) = 0 ⇔ y + 1 = 0

Câu 15: Đáp án: B

Ta có:

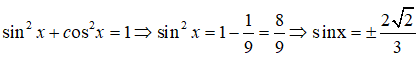
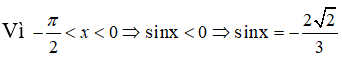
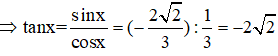
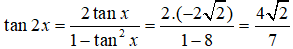
Câu 16: Đáp án: A

Ta có:

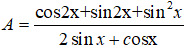
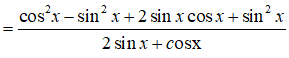
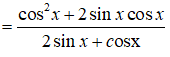
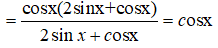
Câu 17: Đáp án: C

Ta có:

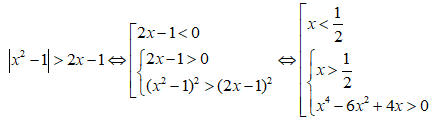
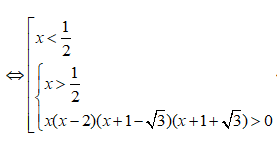
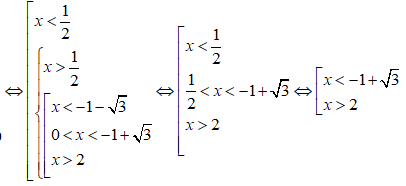
Vậy tập nghiệm của bất phương trình là: (-∞;-1+√3) ∪ (2;+∞)

Câu 18: Đáp án: D

Khoảng cách từ điểm M(3;-4) đến đường thẳng d: 3x - 4y - 1 = 0 là:

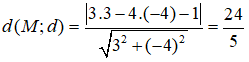
Câu 19: Đáp án: C

Ta có:

sin⁶⁡x + cos⁶x = (sin²⁡x)³ + (cos²x)³

= (s⁡in²x + cos²⁡x)(sin⁴⁡x - sin²⁡xcos²x + cos⁴x)

= sin⁴⁡ x - sin²⁡xcos²⁡ x + cos⁴ x

= (sin²⁡x + cos²x)² - 3 sin²⁡xcos²x

= 1 - 3sin²⁡xcos²⁡x

= 1 - (3/4) sin²⁡2x

Vì

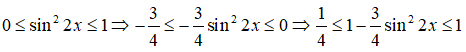
Vậy giá trị nhỏ nhất của sin⁶⁡ x + cos⁶x là 1/4

Dấu “=” xảy ra ⇔ sin²⁡2x = 1 ⇔ sin⁡2x = 1 hoặc sin⁡2x = -1

Câu 20: Đáp án: B

Phương trình tham số của đường thẳng đi qua A(2;7) có vecto chỉ phương

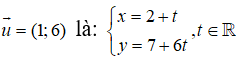
Phần II: Tự luận

Câu 1:

a) Ta có:

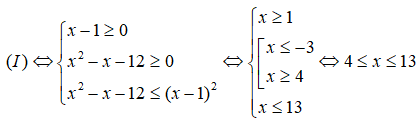
Vậy tập nghiệm của bất phương trình là: [4;13]

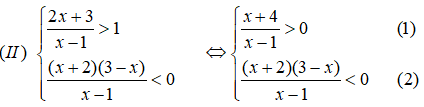
Ta có bảng xét dấu vế trái của bất phương trình (1):

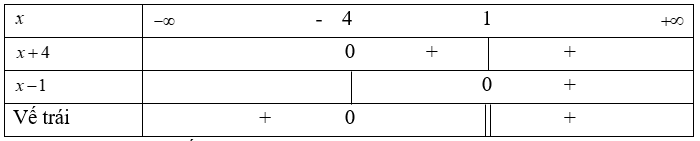
Vậy tập nghiệm của bất phương trình (1) là: (-∞;-4) ∪ (1;+∞)

Ta có bảng xét dấu vế trái của bất phương trình (2) là:

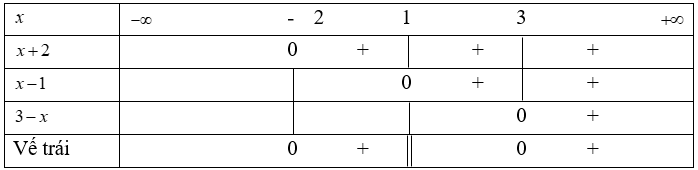
Vậy tập nghiệm của bất phương trình (2) là: (-∞;-2) ∪ (1;3)

Vậy tập nghiệm của hệ bất phương trình là: (-∞;-4) ∪ (1;3)

b) Để hàm số có tập xác định D = R thì (m + 10)x² - 2(m - 2)x + 1 ≥ 0, ∀x

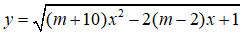
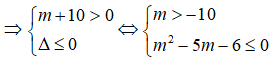
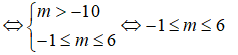
Vậy với -1 ≤ m ≤ 6 thì hàm số có tập xác định D = R

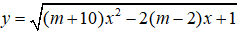
Câu 2:

Ta có:

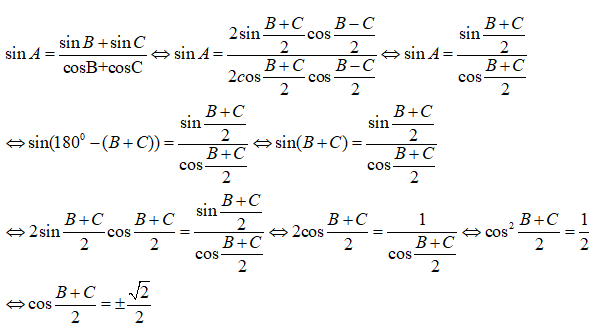
Vì:

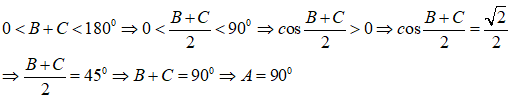
Suy ra, tam giác ABC vuông tại A

Câu 3:

Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)

Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)

Vậy đường thẳng Δ có dạng: x+y-3=0

Vì đường tròn có tâm I thuộc d nên I(a;-a)

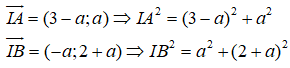
Vì đường tròn đi qua A, B nên IA² = IB² ⇒ (3 - a)² + a² = a² + (2 + a)² ⇔ (3 - a)² = (2 + a)²

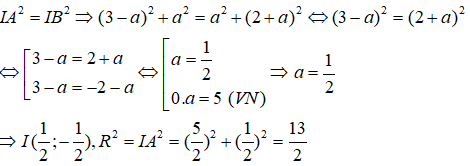
Vậy phương trình đường tròn có dạng:

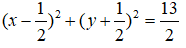
Ta có:

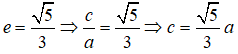
Giả sử elip (E) có dạng:

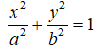
Vì (E) đi qua B nên:

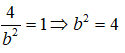
Mà

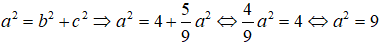
Vậy phương trình chính tắc của elip (E) là:

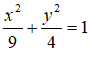
Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Năm học 2023

Môn: Ngữ Văn 10

Thời gian làm bài: 90 phút

(Đề số 7)

Phần I: Trắc nghiệm

Câu 1: Đường thẳng d đi qua hai điểm A(8;0), B(0;7) có phương trình là:

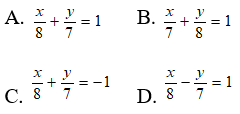
Câu 2: Số đo tính theo đơn vị rađian của góc 135^o là:

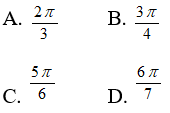
Câu 3: Tập nghiệm của bất phương trình x² - 3x - 4 < 0

A. (-∞;-1) ∪ (4;+∞) B.(-∞;-1)

C. (4;+∞) D. (-1;4)

Câu 4: Góc giữa hai đường thẳng d: x + y + 2 = 0 và d': y + 1 = 0 có số đo bằng:

A. 90^o B. 60^o

C. 45^o D. 30^o

Câu 5: Đường tròn (C): x² + y² - 4x + 6y - 12 = 0 có tâm I và bán kính R là:

A. I(-2;3), R = 25 B. I(-2;3), R = 5

C. I(2;-3), R = 25 D. I(2;-3), R = 5

Câu 6: Cho đường thẳng Δ: x + 2y + m = 0 và đường tròn (C): x² + y² = 9. Giá trị của m để Δ tiếp xúc với (C) là:

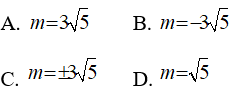
Câu 7: Cho hai điểm M(3;2), N(-1;-4). Đường trung trực của MN có phương trình là:

A. 2x + 3y + 1 = 0 B. 2x + 3y - 1 = 0

C. 2x - 3y + 1 = 0 D. 2x - 3y - 1 = 0

Câu 8: Đường elip có tâm sai bằng:

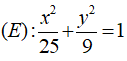
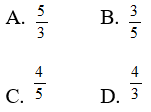
Câu 9: Cho . Khi đó, bằng:

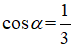
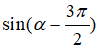
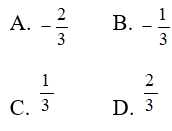
Câu 10: Đường elip có tiêu cự bằng:

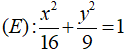
A. √7 B. 2√7

C. 5 D. 10

Câu 11: Cho s⁡inx + cosx = √2. Khi đó sin⁡2 x có giá trị bằng:

A. -1 B. 0

C. 1 D. 2

Câu 12: Tập nghiệm của bất phương trình là:

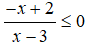
A. (-∞;2] ∪ [3;+∞) B. (-∞;2] ∪ (3;+∞)

C. (-∞;2) ∪ [3;+∞) D. [2;3]

Câu 13: Với mọi số thực α, ta có bằng:

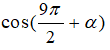
A. sin⁡α B. cosα

C. -sin⁡α D. -cosα

Câu 14: Cho . Khi đó, cos2α nhận giá trị bằng:

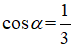
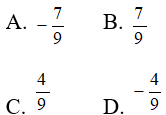
Câu 15: Tập nghiệm của bất phương trình |2x-1| < 3x-2 là:

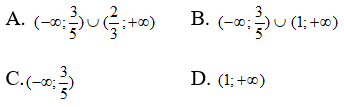
Câu 16: Hàm số có tập xác định:

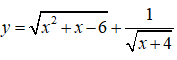
A. D = [-4;-3] ∪ [2;+∞) B. D = (-4;+∞)

C. D = (-∞;-3] ∪ [2;+∞) D. D = (-4;-3] ∪ [2;+∞)

Câu 17: Điều tra về số con của 30 gia đình ở khu vực Hà Đông - Hà Nội kết quả thu được như sau:

Giá trị ( số con)	0	1	2	3	4
Tần số	1	7	15	5	2	N = 30

Số trung bình x của mẫu số liệu trên bằng:

A. 1 B. 1,5

C. 2 D. 3

Câu 18: Với a, b là hai số thực tùy ý. Đẳng thức nào sau đây sai?

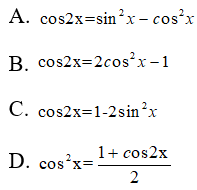
Câu 19: Giá trị của tham số m để d:x-2y+3=0 và song song với nhau là:

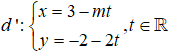
A. m = 1 B. m = -1

C. m = 4 D. m = -4

Câu 20: Cho hypebol . Diện tích hình chữ nhật cơ sở là:

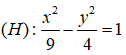
A. 6 B. 12

C. 18 D. 24

Phần II: Tự luận

Câu 1: Giải các bất phương trình sau:

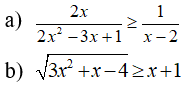
Câu 2: Cho

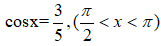
Tính giá trị biểu thức sau:

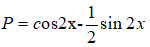
Câu 3: Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm A(1;2), B(3;-1), C(-2;1)

a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC

b) Viết phương trình đường tròn đường kính AB

Câu 4: Giải phương trình:

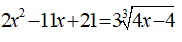
Đáp án & Hướng dẫn giải

Phần I: Trắc nghiệm

1	2	3	4	5
A	B	D	C	D
6	7	8	9	10
C	A	C	C	B
11	12	13	14	15
C	B	C	A	D
16	17	18	19	20
D	C	A	C	D

Câu 1: Đáp án: A

Phương trình đoạn chắn đi qua hai điểm A(8;0), B(0;7) là:

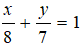
Câu 2: Đáp án: B

Số đo tính theo đơn vị rađian của góc 135^o là:

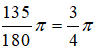
Câu 3: Đáp án: D

x² - 3x - 4 < 0 ⇔ (x + 1)(x - 4) < 0 ⇔ -1 < x < 4

Câu 4: Đáp án: C

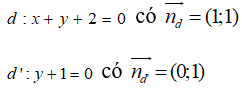
Gọi α là góc giữa hai đường thẳng d và d’

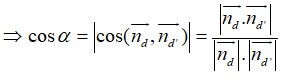
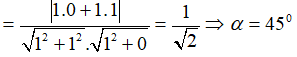
Câu 5: Đáp án: D

(C): x² + y² - 4x + 6y - 12 = 0 ⇔ (x - 2)² + (y + 3)² = 25

Vậy đường tròn (C) có I(2;-3), R = 5

Câu 6: Đáp án: C

(C): x² + y² = 9 có I(0;0), R = 3

Để Δ tiếp xúc với đường tròn (C) thì

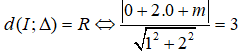
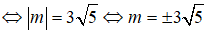
Câu 7: Đáp án: A

M(3;2), N(-1;-4)

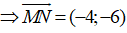
Gọi I là trung điểm của MN ⇒ I(1;-1)

Đường thẳng trung trực của MN là đường thẳng đi qua I và nhận vecto MN làm vecto pháp tuyến:

MN: -4(x - 1) - 6(y + 1) = 0 ⇔ 2x + 3y + 1 = 0

Câu 8: Đáp án: C

Ta có:

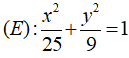
⇒ a² = 25, b² = 9

Mà a² = b² + c² ⇒ c² = a² - b² = 25 - 9 = 16 ⇒ c = 4

Vậy

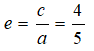
Câu 9: Đáp án: C

Ta có:

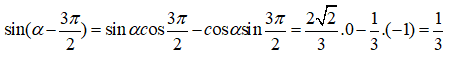
Câu 10: Đáp án: B

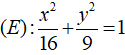
⇒ a² = 16, b² = 9

Mà c² = a² - b² = 16 - 9 = 7 ⇒ c = √7 ⇒ 2c = 2√7

Câu 11: Đáp án: C

Ta có: s⁡inx + cosx = √2 ⇒ (s⁡inx + cosx)² = 2

⇔ sin²x + 2sin⁡xcos⁡x + cos²⁡ x = 2

⇔ 1 + sin⁡2x = 2

⇔ sin⁡2x = 1

Câu 12: Đáp án: B

Giải bất phương trình

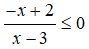
Ta có bảng xét dấu vế trái của bất phương trình:

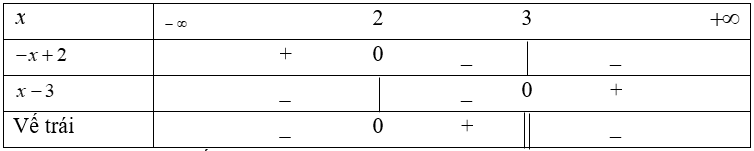
Vậy tập nghiệm của bất phương trình là: (-∞;2] ∪ (3;+∞)

Câu 13: Đáp án: C

Ta có:

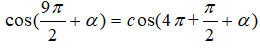
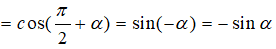
Câu 14: Đáp án: A

Ta có:

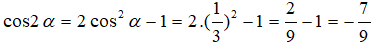
Câu 15: Đáp án: D

Ta có:

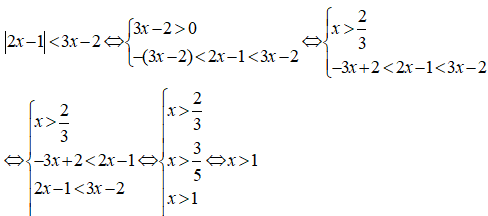
Câu 16: Đáp án: D

Hàm số xác định khi và chỉ khi:

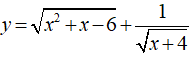
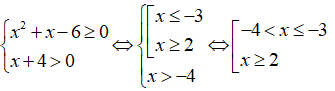
Vậy tập xác định của hàm số là: D = (-4;-3] ∪ [2;+∞)

Câu 17: Đáp án: C

Ta có:

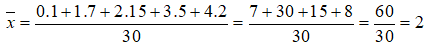
Câu 18: Đáp án: A

Ta có: cos2x = cos²x - sin²⁡x

Vậy đáp án A sai

Câu 19: Đáp án: C

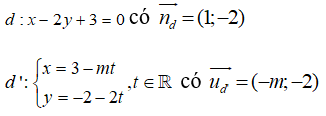
Vì d//d'

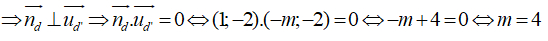
Câu 20: Đáp án: D

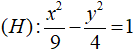
có a² = 9 ⇒ a = 3, b² = 4 ⇒ b = 2

Hình chữ nhật cơ sở của hypebol (H) là hình chữ nhật với độ dài hai cạnh là 6 và 4. Vậy diện tích hình chữ nhật cơ sở là: 6.4 = 24

Phần II: Tự luận

Câu 1:

Giải các bất phương trình sau:

Ta có:

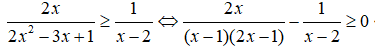
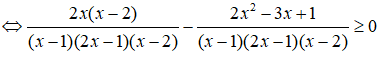
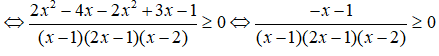
Ta có bảng xét dấu vế trái của bất phương trình:

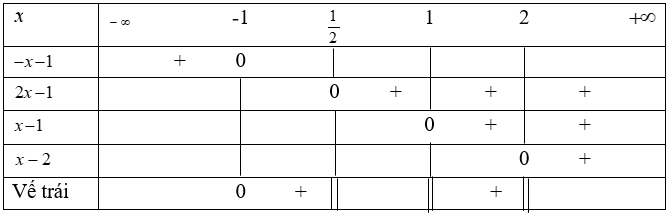
Vậy tập nghiệm của bất phương trình là:

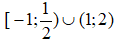
Ta có:

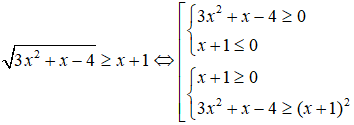
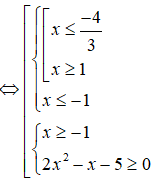
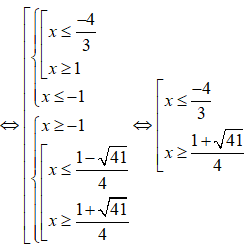
Vậy tập nghiệm của bất phương trình là:

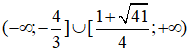
Câu 2:

Ta có:

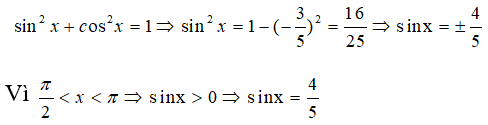
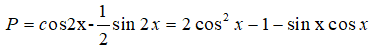
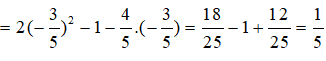
Vậy giá trị của P là:

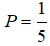
Câu 3:

a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC

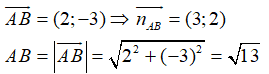
Phương trình tổng quát của AB là: 3(x - 1) + 2(y - 2) = 0 ⇔ 3x + 2y - 7 = 0

Kẻ CH ⊥ AB, (H ∈ AB)

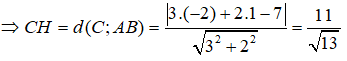
Diện tích tam giác ABC là:

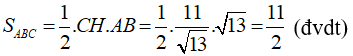
b) Viết phương trình đường tròn đường kính AB

Gọi I là trung điểm của AB

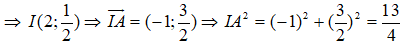
Đường tròn đường kính AB là đường tròn tâm I bán kính IA:

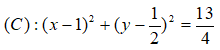
Câu 4:

Ta thấy:

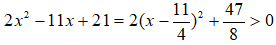
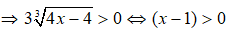
Áp dụng bất đẳng thức Cô – si ta có:

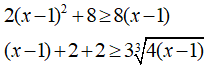
Cộng vế với vế ta được:

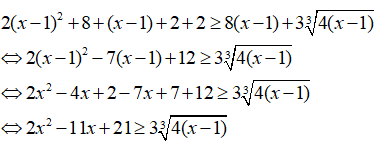
Dấu “=” xảy ra khi và chỉ khi x - 1 = 2 ⇔ x = 3

Vậy x = 3 là nghiệm của phương trình.