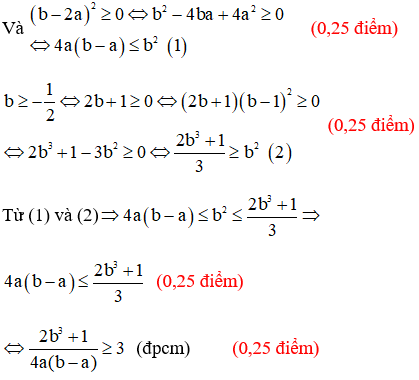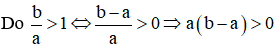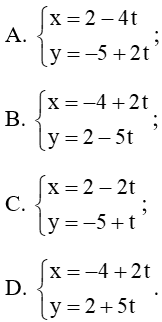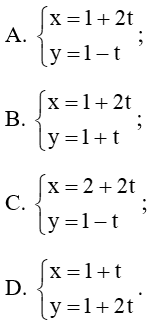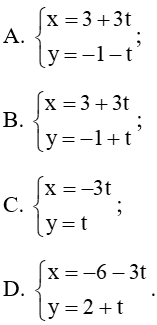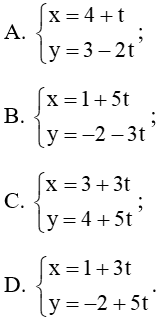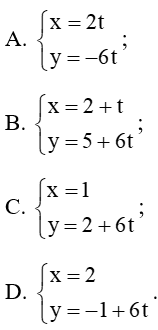Đề thi Toán lớp 10 Giữa học kì 2 năm 2023 có đáp án (4 đề - Sách mới)
Đề thi Toán lớp 10 Giữa học kì 2 năm 2023 có đáp án (4 đề - Sách mới)
Haylamdo biên soạn và sưu tầm Đề thi Toán lớp 10 Giữa học kì 2 năm 2023 có đáp án Kết nối tri thức, Cánh diều, Chân trời sáng tạo được tổng hợp chọn lọc từ đề thi môn Toán 10 của các trường trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong các bài thi Toán lớp 10.
- Ma trận Đề thi Toán lớp 10 Giữa học kì 2
- Đề thi Toán lớp 10 Giữa học kì 2 (Đề 1)
- Đề thi Toán lớp 10 Giữa học kì 2 (Đề 2)
- Đề thi Toán lớp 10 Giữa học kì 2 (Đề 3)
- Đề thi Toán lớp 10 Giữa học kì 2 (Đề 4)
- Đề thi Toán lớp 10 Giữa học kì 2 (Đề 5)
- Đề thi Toán lớp 10 Giữa học kì 2 (Đề 6)
- Đề thi Toán lớp 10 Giữa học kì 2 (Đề 7)
Đề thi Toán lớp 10 Giữa học kì 2 năm 2023 có đáp án (4 đề - Sách mới)
Xem thử Đề Toán 10 GK2 KNTT Xem thử Đề Toán 10 GK2 Cánh diều Xem thử Đề Toán 10 GK2 CTST
Chỉ 100k mua trọn bộ Đề thi Toán 10 Giữa kì 2 (mỗi bộ sách) bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án
Đề thi Giữa kì 2 Toán 10 Chân trời sáng tạo có đáp án (4 đề)

Ma trận đề thi Giữa học kì 2
Câu hỏi trắc nghiệm: 35 câu (70%)
Câu hỏi tự luận: 3 câu (30%)
|
TT |
Nội dung kiến thức |
Đơn vị kiến thức |
Mức độ nhận thức |
Tổng |
% tổng điểm |
|||||||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
Số CH |
Thời gian (phút) |
|||||||||
|
Số CH |
Thời gian (phút) |
Số CH |
Thời gian (phút) |
Số CH |
Thời gian (phút) |
Số CH |
Thời gian (phút) |
TN |
TL |
|||||
|
1 |
HÀM SỐ, ĐỒ THỊ VÀ ỨNG DỤNG |
1.1. Hàm số |
3 |
3 |
2 |
4 |
|
|
|
|
5 |
|
|
|
|
1.2. Hàm số bậc hai |
3 |
3 |
2 |
4 |
1* |
10 |
|
|
5 |
1* |
||||
|
1.3. Dấu của tam thức bậc hai |
3 |
3 |
2 |
4 |
|
|
1** |
10 |
5 |
1** |
||||
|
1.4. Phương trình quy về phương trình bậc hai |
2 |
3 |
2 |
5 |
1* |
10 |
|
|
4 |
1* |
|
|
||
|
2 |
PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG |
2.1. Phương trình đường thẳng |
3 |
3 |
3 |
8 |
1* |
10 |
|
|
6 |
1* |
|
|
|
2.2. Vị trí tương đối giữa hai đường thẳng, góc và khoảng cách |
3 |
5 |
2 |
5 |
|
|
|
|
5 |
|
|
|
||
|
2.3. Đường tròn |
3 |
5 |
2 |
5 |
|
|
1** |
10 |
5 |
1** |
|
|
||
|
Tổng |
|
20 |
25 |
15 |
35 |
2 |
20 |
1 |
10 |
35 |
3 |
|
|
|
|
Tỉ lệ (%) |
|
40 |
30 |
20 |
10 |
70 |
30 |
|
100 |
|||||
|
Tỉ lệ chung (%) |
|
70 |
30 |
100 |
|
100 |
||||||||
Lưu ý:
- Các câu hỏi ở cấp độ nhận biết và thông hiểu là các câu hỏi trắc nghiệm khách quan 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
- Các câu hỏi ở cấp độ vận dụng và vận dụng cao là các câu hỏi tự luận.
- Số điểm tính cho 1 câu trắc nghiệm là 0,2 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ điểm được quy định trong ma trận.
- Trong nội dung kiến thức:
+ (1*): Chỉ được chọn hai câu mức độ vận dụng thuộc hai trong ba nội dung.
+ (1**): Chỉ được chọn một câu mức độ vận dụng cao ở một trong hai nội dung.
BẢNG ĐẶC TẢ KĨ THUẬT ĐỀ KIỂM TRA GIỮA HỌC KÌ 2
|
TT |
Nội dung kiến thức |
Đơn vị kiến thức |
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá |
Số câu hỏi theo mức độ nhận thức |
|||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
||||
|
1 |
HÀM SỐ, ĐỒ THỊ VÀ ỨNG DỤNG |
1.1. Hàm số |
Nhận biết: - Nhận biết được hàm số được cho bằng bảng, bằng biểu đồ, bằng công thức hoặc mô tả bằng lời; - Nhận biết giá trị của hàm số dựa vào bảng giá trị; - Nhận biết được khoảng đồng biến và nghịch biến dựa vào đồ thị hàm số. Thông hiểu: - Tìm được tập xác định, tập giá trị của hàm số: hàm số phân thức hoặc hàm số chứa căn; - Tính giá trị của hàm số. |
3 |
2 |
|
|
|
1.2. Hàm số bậc hai |
Nhận biết: - Nhận biết được hàm số bậc hai và các hệ số của hàm số bậc hai; - Nhận dạng được đồ thị hàm số bậc hai; - Nhận được các yếu tố cơ bản của đồ thị hàm số bậc hai: đỉnh, trục đối xứng, .... Thông hiểu: - Xác định khoảng đồng biến, nghịch biến; giá trị nhỏ nhất, lớn nhất của hàm số bậc hai; - Xác định hàm số bậc hai khi biết một số yếu tố. Vận dụng: - Vận dụng được kiến thức về hàm số bậc hai và đồ thị vào giải quyết bài toán thực tiễn. |
3 |
2 |
1 |
|
||
|
1.3. Dấu của tam thức bậc hai
|
Nhận biết: - Nhận biết được tam thức bậc hai; - Nhận biết dấu của tam thức bậc hai; - Xác định hệ số a, b, c của tam thức bậc hai cho trước. Thông hiểu: - Tìm được các khoảng hoặc nửa khoảng để tam thức bậc hai nhận giá trị dương (âm, không dương, không âm, ...); - Giải được các bất phương trình bậc hai. Vận dụng cao: - Vận dụng bất phương trình bậc hai vào giải quyết bài toán thực tiễn. |
3 |
2 |
|
1 |
||
|
1.4. Phương trình quy về phương trình bậc hai |
Nhận biết: - Nhận biết nghiệm của phương trình dạng: . Thông hiểu: - Biết được số nghiệm của phương trình dạng: . Vận dụng: - Giải được phương trình quy về phương trình bậc hai; - Vận dụng trong bài toán thực tế có liên quan. |
2 |
2 |
1 |
|
||
|
2 |
PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG |
2.1. Phương trình đường thẳng |
Nhận biết: - Vectơ pháp tuyến hoặc vectơ chỉ phương của đường thẳng; - Điểm thuộc (không thuộc) đường thẳng; - Nhận dạng PTTS của đường thẳng khi biết đường thẳng đó đi qua 1 điểm và nhận 1 vectơ chỉ phương. Thông hiểu: - Xác định được PTTQ của đường thẳng khi biết đường thẳng đó đi qua 1 điểm và nhận 1 vectơ pháp tuyến; - Viết phương trình đường thẳng đi qua 2 điểm cho trước; - Chuyển dạng phương trình đường thẳng (từ dạng tham số sang dạng tổng quát, hoặc từ dạng tổng quát về dạng tham số). Vận dụng: - Liên hệ được các kiến thức tổng hợp để viết phương trình đường thẳng ở dạng phức tạp; - Vận dụng kiến thức về phương trình đường thẳng để giải một số bài toán thực tiễn có liên quan. |
3 |
3 |
1 |
|
|
2.2. Vị trí tương đối của 2 đường thẳng |
Nhận biết: - Nhận biết vị trí tương đối giữa hai đường thẳng; - Nhận biết công thức tính khoảng cách từ một điểm đến một đường thẳng; - Nhận biết công thức tính góc giữa hai đường thẳng. Thông hiểu: - Tính khoảng cách từ một điểm đến một đường thẳng; - Tính góc giữa hai đường thẳng; - Xác định vị trí tương đối giữa hai đường thẳng; - Tìm giao điểm của 2 đường thẳng; - Tìm điều kiện m để 2 đường thẳng song song hoặc vuông góc (trong trường hợp đơn giản). |
3 |
2 |
|
|
||
|
2.3. Đường tròn |
Nhận biết: - Nhận biết phương trình đường tròn; - Xác định được tâm và bán kính đường tròn biết phương trình của nó; - Xác định được phương trình đường tròn biết tâm và bán kính cho trước. Thông hiểu: - Xác định được phương trình đường tròn khi biết tâm và điểm đi qua; - Xác định được phương trình đường tròn khi biết đường kính AB (A, B có tọa độ cho trước); - Xác định được phương trình đường tròn khi biết tâm và tiếp xúc với đường thẳng cho trước; - Phương trình tiếp tuyến của đường tròn tại điểm thuộc đường tròn. Vận dụng cao: - Tổng hợp các kiến thức về phương trình đường tròn. |
3 |
2 |
|
1 |
||
|
|
|
|
20 |
15 |
2 |
1 |
|
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 2 - Kết nối tri thức
Năm học 2023
Môn: Toán lớp 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 1)
I. Trắc nghiệm (7 điểm)
Câu 1. Trong các công thức sau, công thức nào không biểu diễn y là hàm số của x?
A. 2x + y = 5;
B. + y = 5;
C. y = ;
D. 2x2 – 3y2 = 0.
Câu 2. Cho hàm số dưới dạng bảng như sau:
x |
0 |
1 |
2 |
3 |
4 |
y |
0 |
1 |
4 |
9 |
16 |
Giá trị của hàm số y tại x = 1 là
A. 1;
B. 4;
C. 9;
D. 16.
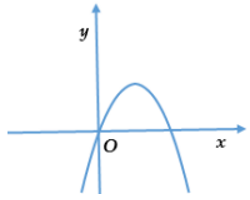
Câu 3. Cho hàm số y = f(x) có đồ thị như hình dưới.
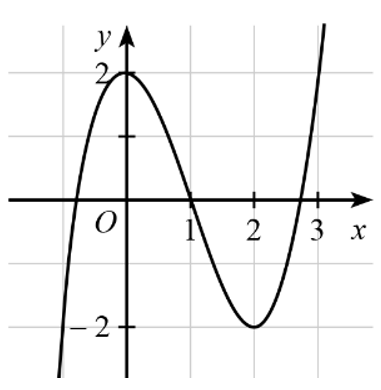
Hàm số trên nghịch biến trên khoảng
A. (– ∞; 2);
B. (2; + ∞);
C. (0; 2);
D. (– ∞; 0).
Câu 4. Hàm số có tập xác định là
A. (– 2; 5);
B. [– 2; 5];
C. (– ∞; – 2] ∪ [5; + ∞);
D. ℝ \ {– 2; 5}.
Câu 5. Cho hàm số 
A. – 1998;
B. 0;
C. 1;
D. Không tồn tại.
Câu 6. Trong các hàm số sau, hàm số nào không phải là hàm số bậc hai?
A. y = x2 – 2x + 1;
B. y = (x2)2 – 3x2 + 6;
C. y = x2 + 5x + 9;
D. y = 10 – 4x – x2.
Câu 7. Cho đồ thị hàm số bậc hai y = ax2 + bx + c (a ≠ 0) như hình vẽ sau.
Điều kiện của hệ số a của hàm số bậc hai này là
A. a = 1;
B. a > 1;
C. a > 0;
D. a < 0.
Câu 8. Đồ thị của hàm số bậc hai y = – x2 + 5 + 3x có trục đối xứng là
A. ;
B. ;
C. x = 3;
D. x = 5.
Câu 9. Cho hàm số bậc hai f(x) = – 2x2 – x + 1. Giá trị lớn nhất của hàm số là
A. ;
B. ;
C. ;
D. Không tồn tại.
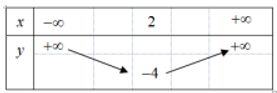
Câu 10. Cho hàm số bậc hai có bảng biến thiên như sau:
Công thức hàm số bậc hai trên là
A. y = – x2 + 4x;
B. y = x2 + 4x;
C. y = x2 – 4x;
D. y = – x2 – 4x.
Câu 11. Biểu thức nào dưới đây không phải là tam thức bậc hai?
A. f(x) = 2x2 + 5x – 3;
B. f(x) = x2 – 9;
C. f(x) = 32x2 + 3x + 4;
D. f(x) = x4 – 2x2 + 5.
Câu 12. Cho tam thức bậc hai f(x) = ax2 + bx + c, (a ≠ 0) và ∆ = b2 – 4ac. Mệnh đề nào sau đây đúng?
A. Nếu ∆ > 0 thì f(x) luôn cùng dấu với hệ số a, với mọi x ∈ ℝ;
B. Nếu ∆ < 0 thì f(x) luôn trái dấu với hệ số a, với mọi x ∈ ℝ;
C. Nếu ∆ = 0 thì f(x) luôn cùng dấu với hệ số a, với mọi x ∈ ℝ \ ;
D. Nếu ∆ < 0 thì f(x) luôn cùng dấu với hệ số b, với mọi x ∈ ℝ.
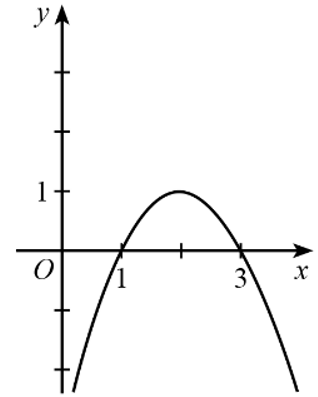
Câu 13. Cho hàm số y = f(x) có đồ thị như hình dưới đây.
Trong các phát biểu sau, phát biểu nào sai?
A. f(x) < 0 khi và chỉ khi x ∈ (1; 3);
B. f(x) ≤ 0 khi và chỉ khi x ∈ (– ∞; 1] ∪ [3; + ∞);
C. f(x) > 0 khi và chỉ khi x ∈ (1; 3);
D. f(x) ≥ 0 khi và chỉ khi x ∈ [1; 3].
Câu 14. Tam thức nào sau đây luôn dương với mọi giá trị của x?
A. x2 – 10x + 2;
B. x2 – 2x – 10;
C. x2 – 2x + 10;
D. – x2 + 2x + 10.
Câu 15. Gọi S là tập nghiệm của bất phương trình x2 – 8x + 7 ≥ 0. Tromg các tập hợp sau, tập nào không là tập con của S?
A. (– ∞; 0];
B. [6; + ∞);
C. [8; + ∞];
D. (– ∞; – 1].
Câu 16. Trong các phát biểu sau, phát biểu nào là đúng?
A. Tập nghiệm của phương trình là tập nghiệm của phương trình ax2 + bx + c = (dx + e)2;
B. Tập nghiệm của phương trình là tập hợp các nghiệm của phương trình ax2 + bx + c = (dx + e)2 thỏa mãn bất phương trình dx + e ≥ 0;
C. Mọi nghiệm của phương trình ax2 + bx + c = (dx + e)2 đều là nghiệm của phương trình ;
D. Tập nghiệm của phương trình là tập hợp các nghiệm của phương trình ax2 + bx + c = (dx + e)2 thỏa mãn bất phương trình ax2 + bx + c ≥ 0.
Câu 17. Trong các phát biểu sau, phát biểu nào là đúng?
A. Tập nghiệm của phương trình là tập nghiệm của phương trình ax2 + bx + c = dx2 + ex + f;
B. Tập nghiệm của phương trình là tập nghiệm của phương trình (ax2 + bx + c)2 = (dx2 + ex + f)2;
C. Mọi nghiệm của phương trình ax2 + bx + c = dx2 + ex + f đều là nghiệm của phương trình ;
D. Tập nghiệm của phương trình là tập hợp các nghiệm của phương trình ax2 + bx + c = dx2 + ex + f thỏa mãn bất phương trình ax2 + bx + c ≥ 0 (hoặc dx2 + ex + f ≥ 0).
Câu 18. Phương trình có số nghiệm là
A. 0;
B. 1;
C. 2;
D. 3.
Câu 19. Cho phương trình (1). Để phương trình (1) có nghiệm thì m ∈ [a; b]. Giá trị a2 + b2 bằng
A. 2;
B. 4;
C. 1;
D. 3.
Câu 20. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: – x + 2y + 7 = 0. Vectơ pháp tuyến của đường thẳng d là
A. ;
B. ;
C. ;
D. .
Câu 21. Điểm nào dưới đây không thuộc đường thẳng d: 2x – 5y + 3 = 0?
A. A(1; 1);
B. B;
C. C;
D. D(2; 3).
Câu 22. Phương trình tham số của đường thẳng ∆ đi qua điểm A(– 4; 2) và nhận làm vectơ chỉ phương là
Câu 23. Phương trình tổng quát của đường thẳng d đi qua điểm A(1; – 3) và nhận làm vectơ pháp tuyến là
A. 2x – 7y + 23 = 0;
B. – 2x + 7y – 23 = 0;
C. 2x – 7y – 23 = 0;
D. – 2x – 7y + 23 = 0.
Câu 24. Cho đường thẳng d có phương trình tổng quát: x + 2y – 3 = 0. Phương trình tham số của đường thẳng d là
Câu 25. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(3; – 1) và B(– 6; 2). Phương trình nào sau đây không phải là phương trình tham số của đường thẳng AB?
Câu 26. Trong mặt phẳng tọa độ, xét hai đường thẳng
∆1: a1x + b1y + c1 = 0; ∆2: a2x + b2y + c2 = 0.
và hệ phương trình: 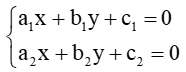
Khi đó, ∆1 trùng với ∆2 khi và chỉ khi
A. hệ (*) có vô số nghiệm;
B. hệ (*) vô nghiệm;
C. hệ (*) có nghiệm duy nhất;
D. hệ (*) có hai nghiệm.
Câu 27. Cho điểm M(x0; y0) và đường thẳng ∆: ax + by + c = 0. Khoảng cách từ điểm M đến đường thẳng ∆, kí hiệu là d(M, ∆), được tính bởi công thức
A. ;
B. ;
C. ;
D. .
Câu 28. Trong mặt phẳng tọa độ, cho hai đường thẳng
∆1: a1x + b1y + c1 = 0; ∆2: a2x + b2y + c2 = 0,
với các vectơ pháp tuyến và tương ứng. Khi đó góc φ giữa hai đường thẳng đó được xác định bởi công thức
A. ;
B. ;
C. ;
D. .
Câu 29. Khoảng cách từ điểm M(5; – 1) đến đường thẳng d: 3x + 2y + 13 = 0 là
A. ;
B. ;
C. 26;
D. .
Câu 30. Góc giữa hai đường thẳng a: 6x – 5y + 15 = 0 và b: 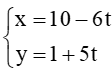
A. 30°;
B. 90°;
C. 60°;
D. 45°.
Câu 31. Phương trình nào sau đây là phương trình đường tròn?
A. x2 + 2y2 – 4x – 8y + 1 = 0;
B. x2 + y2 – 4x + 6y – 12 = 0;
C. x2 + y2 – 2x – 8y + 20 = 0;
D. 4x2 + y2 – 10x – 6y – 2 = 0.
Câu 32. Đường tròn (x + 3)2 + (y – 4)2 = 16 có tâm là
A. I(3; 4);
B. I(3; – 4);
C. I(– 3; 4);
D. I(– 3; – 4).
Câu 33. Phương trình nào sau đây là phương trình của đường tròn tâm I(1; 2), bán kính bằng 5?
A. x2 + y2 – 2x – 4y – 20 = 0;
B. x2 + y2 + 2x + 4 + 20 = 0;
C. x2 + y2 + 2x + 4y – 20 = 0;
D. x2 + y2 – 2x – 4y + 20 = 0.
Câu 34. Phương trình đường tròn đường kính AB với A(1; 3) và B(5; – 1) là
A. (x + 3)2 + (y – 1)2 = 8;
B. (x + 3)2 + (y + 1)2 = 8;
C. (x – 3)2 + (y + 1)2 = 8;
D. (x – 3)2 + (y – 1)2 = 8.
Câu 35. Trong mặt phẳng tọa độ, cho đường tròn (C): x2 + y2 – 2x – 4y – 4 = 0 và điểm A(1; 5). Tiếp tuyến của đường tròn (C) tại điểm A có phương trình là
A. y – 5 = 0;
B. y + 5 = 0;
C. x + y – 5 = 0;
D. x – y – 5 = 0.
II. Tự luận (3 điểm)
Bài 1. (1 điểm) Giải các phương trình sau:
a) ;
b) .
Bài 2. (1 điểm) Viết phương trình tổng quát của đường thẳng
a) đi qua M(– 1; – 4) và song song với đường thẳng 3x + 5y – 2 = 0;
b) đi qua N(1; 1) và vuông góc với đường thẳng 2x + 3y + 7 = 0.
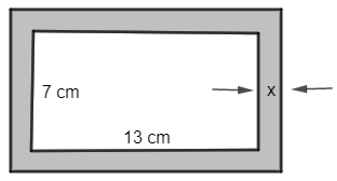
Bài 3. (1 điểm) Hà dự định làm một khung ảnh hình chữ nhật sao cho phần trong của khung là hình chữ nhật có kích thước 7 cm × 13 cm, độ rộng viền xung quanh là x cm (như hình vẽ). Diện tích của viền khung ảnh không vượt quá 44 cm2. Hỏi độ rộng viền khung ảnh lớn nhất là bao nhiêu xen-ti-mét?
-----HẾT-----
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 2 - Cánh diều
Năm học 2023
Môn: Toán lớp 10
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 2)
I. Trắc nghiệm (7 điểm)
Câu 1. Giả sử một công việc có thể được tiến hành theo hai phương án A và B. Phương án A có thể thực hiện bằng n cách, phương án B có thể thực hiện bằng m cách không trùng với cách nào của phương án A. Khi đó:
A. Công việc có thể được thực hiện bằng m.n cách;
B. Công việc có thể được thực hiện bằng cách;
C. Công việc có thể được thực hiện bằng m + n cách;
D. Công việc có thể thực hiện bằng cách.
Câu 2. Có 8 quyển sách khác nhau và 6 quyển vở khác nhau. Số cách chọn một trong các quyển đó là
A. 6;
B. 8;
C. 14;
D. 48.
Câu 3. Từ các số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự mà mỗi số có 6 chữ số khác nhau và chữ số 2 đứng cạnh chữ số 3?
A. 192;
B. 202;
C. 211;
D. 180.
Câu 4. Có 3 học sinh nữ và 2 học sinh nam.Ta muốn sắp xếp vào một bàn dài có 5 ghế ngồi. Số cách sắp xếp để 3 học sinh nữ ngồi kề nhau là
A. 34;
B. 46;
C. 36;
D. 26.
Câu 5. Trong một tuần bạn A dự định mỗi ngày đi thăm một người bạn trong 12 người bạn của mình. Hỏi bạn A có thể lập được bao nhiêu kế hoạch đi thăm bạn của mình (thăm một bạn không quá một lần)?
A. 3 991 680;
B. 12!;
C. 35 831 808;
D. 7!.
Câu 6. Đa thức P(x) = 32x5 – 80x4 + 80x3 – 40x2 + 10x – 1 là khai triển của nhị thức nào dưới đây?
A. (1 – 2x)5;
B. (1 + 2x)5;
C. (2x – 1)5;
D. (x – 1)5.
Câu 7. Trong khai triển nhị thức (1 + x)4, xét các khẳng định sau:
I. Gồm có 5 số hạng.
II. Số hạng thứ 2 là 6x.
III. Hệ số của x3 là 4.
Trong các khẳng định trên, ta có:
A. Chỉ I và III đúng;
B. Chỉ II và III đúng;
C. Chỉ I và II đúng;
D. Cả ba đúng.
Câu 8. Trong mặt phẳng tọa độ Oxy, cho vectơ . Tọa độ của vectơ là
A. (– 5; 6);
B. (5; 6);
C. (– 5; – 6);
D. (5; – 6).
Câu 9. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(5; 8), B(9; – 3) và C(1; 1). Tọa độ trọng tâm G của tam giác ABC là
A. (– 5; 2);
B. (5; 2);
C. (15; 6);
D. (6; 15).
Câu 10. Trong mặt phẳng tọa độ Oxy, cho hai vectơ và . Giá trị của m để vectơ vuông góc với vectơ là
A. ;
B. ;
C. m = 1;
D. m = – 1.
Câu 11. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: – 2x + 3y + 10 = 0. Một vectơ chỉ phương của đường thẳng d là
A. ;
B. ;
C. ;
D. .
Câu 12. Phương trình tham số của đường thẳng đi qua hai điểm M(1; – 2) và N(4; 3) là
Câu 13. Cho đường thẳng d có phương trình tham số: 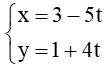
A. 4x – 5y – 7 = 0;
B. 4x + 5y – 17 = 0;
C. 4x – 5y – 17 = 0;
D. 4x + 5y + 17 = 0.
Câu 14. Tọa độ giao điểm của hai đường thẳng x – 3y – 6 = 0 và 3x + 4y – 1 = 0 là
A. ;
B. (– 27; 17);
C. ;
D. (27; – 17).
Câu 15. Với giá trị nào của m thì hai đường thẳng d1: 2x – 3y – 10 = 0 và d2: 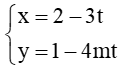
A. ;
B. ;
C. ;
D. .
Câu 16. Khoảng cách từ điểm A(– 3; 2) đến đường thẳng ∆: 3x – y + 1 = 0 là
A. ;
B. ;
C. ;
D. .
Câu 17. Góc giữa hai đường thẳng a: 2x + 5y – 2 = 0 và b: 3x – 7y + 3 = 0 bằng
A. 30°;
B. 135°;
C. 60°;
D. 45°.
Câu 18. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 2), B(3; 1) và C(5; 4). Phương trình nào sau đây là phương trình đường cao kẻ từ A của tam giác ABC?
A. 2x + 3y – 8 = 0;
B. 2x + 3y + 8 = 0;
C. 3x – 2y + 1 = 0;
D. 2x + 3y – 2 = 0.
Câu 19. Cho hai đường thẳng d1: 2x – 3y + 7 = 0 và d2: 4x – 6y + 10 = 0. Chọn khẳng định đúng trong các khẳng định sau.
A. d1 // d2;
B. d1 ⊥ d2;
C. d1 và d2 trùng nhau;
D. d1 và d2 cắt nhau nhưng không vuông góc.
Câu 20. Số hạng không chứa x trong khai triển là
A. 1;
B. 5;
C. 10;
D. 20.
Câu 21. Phương trình đường thẳng đi qua điểm A(2; 5) và song song với đường thẳng d: y = 3x + 4 là
A. y = 3x – 2;
B. y = 3x – 1;
C. y = ;
D. y = – 3x – 1.
II. Tự luận (3 điểm)
Bài 1. (1 điểm) Một hộp có 10 viên bi màu trắng, 20 viên bi màu xanh và 30 viên bi màu đỏ, mỗi viên bi chỉ có một màu. Có bao nhiêu cách chọn ngẫu nhiên 8 trong số các viên bi thuộc hộp đó để được 8 viên bi trong đó có đúng một viên bi màu xanh?
Bài 2. (1 điểm) Không sử dụng máy tính cầm tay, tính các tổng sau:
a) ;
b) .
Bài 3. (1 điểm) Viết phương trình đường thẳng đi qua điểm M(2; – 3)và cắt hai trục tọa độ tại hai điểm Avà B sao cho tam giác OAB vuông cân.
-----HẾT-----
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 2 - Chân trời sáng tạo
Năm học 2023
Môn: Toán lớp 10
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 3)
I. Trắc nghiệm (7 điểm)
Câu 1. Tam thức nào sau đây luôn dương với mọi giá trị của x?
A. x2 – 10x + 2;
B. x2 – 2x – 10;
C. x2 – 2x + 10;
D. – x2 + 2x + 10.
Câu 2. Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0) và ∆ = b2 – 4ac. Cho biết dấu của ∆ khi f(x) luôn cùng dấu với hệ số a với mọi x ∈ ℝ.
A. ∆ < 0;
B. ∆ ≥ 0;
C. ∆ > 0;
D. ∆ = 0.
Câu 3. Số nghiệm nguyên của bất phương trình 2x2 – 3x – 15 ≤ 0 là
A. 5;
B. 6;
C. 7;
D. 8.
Câu 4. Phương trình có hai nghiệm là a và b. Khi đó giá trị của biểu thức T = a + b là
A. 32;
B. 38;
C. 35;
D. 3.
Câu 5. Số nghiệm của phương trình là
A. 0;
B. 1;
C. 2;
D. 3.
Câu 6. Trong hệ tọa độ Oxy, cho . Tọa độ vectơ là
A. ;
B. ;
C. (– 1; 10);
D. (1; – 10).
Câu 7. Cho . Tìm vectơ sao cho .
A. ;
B. ;
C. ;
D. .
Câu 8. Trong mặt phẳng tọa độ Oxy, cho hai điểm B(– 1; 3) và C(3; 1). Tìm tọa độ điểm A sao cho tam giác ABC vuông cân tại A.
A. A(0; 0) hoặc A(2; – 4);
B. A(0; 0) hoặc A(2; 4);
C. A(0; 0) hoặc A(– 2; – 4);
D. A(0; 0) hoặc A(– 2; 4).
Câu 9. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 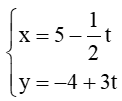
A. ;
B. ;
C. ;
D. .
Câu 10. Phương trình tham số của đường thẳng đi qua hai điểm A(2; – 1) và B(2; 5) là
Câu 11. Trong mặt phẳng tọa độ Oxy, cho điểm M(1; 2). Gọi A và B là hình chiếu của M lên Ox, Oy. Phương trình đường thẳng AB là
A. x + 2y – 1 = 0;
B. 2x + y + 2 = 0;
C. 2x + y – 2 = 0;
D. x + y – 3 = 0.
Câu 12. Đường thẳng d: 51x – 30y + 11 = 0 đi qua điểm nào sau đây?
A. ;
B. ;
C. ;
D. .
Câu 13. Cho hai đường thẳng d1: 2x + 3y + 15 = 0 và d2: x – 2y – 3 = 0. Khẳng định nào sau đây đúng?
A. d1 và d2 cắt nhau và không vuông góc với nhau;
B. d1 và d2 song song với nhau;
C. d1 và d2 trùng nhau;
D. d1 và d2 vuông góc với nhau.
Câu 14. Khoảng cách giữa hai đường thẳng song song ∆1: 6x – 8y + 3 = 0 và ∆2: 3x – 4y – 6 = 0 bằng
A. ;
B. ;
C. 2;
D. .
Câu 15. Xác định tất cả các giá trị của a để góc tạo bởi đường thẳng 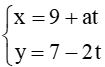
A. a = 1, a = – 14;
B. a = , a = – 14;
C. a = – 2, a = – 14;
D. a = , a = 14.
Câu 16. Phương trình nào sau đây không là phương trình đường tròn?
A. x2 + y2 = 4;
B. 2x2 + 3y2 + 2x + 3y = 9;
C. x2 + y2 + 2x – 1 = 0;
D. x2 + y2 + 4y + 3 = 0.
Câu 17. Tọa độ tâm I và bán kính R của đường tròn (C): x2 + y2 – 2x + 4y + 1 = 0 là
A. I(– 1; 2), R = 4;
B. I(1; – 2), R = 2;
C. I(– 1; 2), R = ;
D. I(1; – 2), R = 4.
Câu 18. Cho đường tròn (C): x2 + y2 – 2x – 4y – 4 = 0 và điểm A(1; 5). Đường thẳng nào trong các đường thẳng dưới đây là tiếp tuyến của đường tròn (C) tại điểm A?
A. y – 5 = 0;
B. y + 5 = 0;
C. x + y – 5 = 0;
D. x – y – 5 = 0.
Câu 19. Cho elip (E) đi qua điểm A(– 3; 0) và có tâm sai . Tiêu cự của (E) bằng
A. 10;
B. 5;
C. ;
D. .
Câu 20. Phương trình chính tắc của parabol (P) có đường chuẩn ∆: x = – 5 là
A. y2 = 20x;
B. y2 = 10x;
C. y2 = – 10x;
D. y2 = – 20x.
Câu 21. Đường hypebol (H) có phương trình chính tắc: có các tiêu điểm là
A. F1(– 5; 0) và F2(5; 0);
B. F1(– 10; 0) và F2(10; 0);
C. F1(; 0) và F2(; 0);
D. F1(– 20; 0) và F2(20; 0).
II. Tự luận (3 điểm)
Bài 1. (1 điểm) Giải các bất phương trình sau:
a) – x2 + 2x + 5 > 2;
b) (1 – 2x)(x2 – x – 1) > 0.
Bài 2. (1 điểm) ChoP(3; 0) và hai đường thẳng d1: 2x – y – 2 = 0 và d2: x + y + 3 = 0. Gọi d là đường thẳng qua P và cắt d1, d2 sao cho PA = PB. Viết phương trình đường thẳng d.
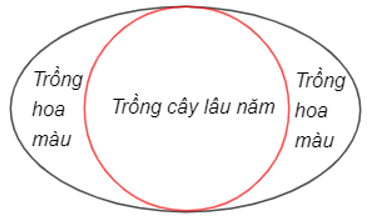
Bài 3. (1 điểm) Ông Hùng có một mảnh vườn hình elip có chiều dài trục lớn và trục nhỏ lần lượt là 60 m và 30 m. Ông chia mảnh vườn ra làm hai nửa bằng một đường tròn tiếp xúc trong với elip với mục đích sử dụng khác nhau (xem hình vẽ). Nửa bên trong đường tròn ông trồng cây lâu năm, nửa bên ngoài đường tròn ông trồng hoa màu. Tính tỉ số diện tích T giữa phần trồng cây lâu năm so với diện tích trồng hoa màu. Biết diện tích hình elip được tính theo công thức S = πab , với a, b lần lượt là nửa độ dài trục lớn và nửa độ dài trục nhỏ. Biết độ rộng của đường Elip là không đáng kể.
-----HẾT-----
Sở Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2023
Môn: Toán lớp 10
Thời gian làm bài: 90 phút
I. Đề bài
Câu 1: Tập xác định của hàm số 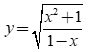 là
là
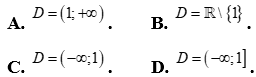
Câu 2: Phương trình 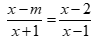 có nghiệm duy nhất khi:
có nghiệm duy nhất khi:
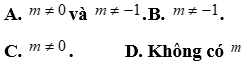
Câu 3: Với giá trị nào của m thì phương trình 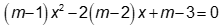 có hai nghiệm
có hai nghiệm 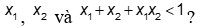
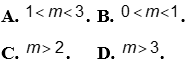
Câu 4: Phương trình 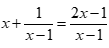 có bao nhiêu nghiệm?
có bao nhiêu nghiệm?
A. 3. B. 2.
C. 1. D. 0.
Câu 5: Tập nghiệm của phương trình: 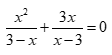 là
là
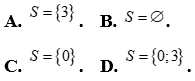
Câu 6: Phương trình 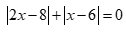 có bao nhiêu nghiệm?
có bao nhiêu nghiệm?
A. 2. B. 1.
C. 0. D. Vô số.
Câu 7: Tính tổng các nghiệm của phương trình 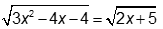
A. 4. B. 3.
C. 5. D. 2.
Câu 8: Tích các nghiệm của phương trình 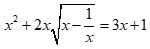 là:
là:
A. 2. B. 3.
C. 0. D. -1.
Câu 9: Chọn khẳng định sai trong các khẳng định sau
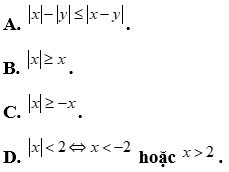
Câu 10: Tìm điều kiện của bất phương trình 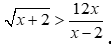 .
.
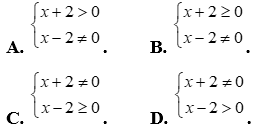
Câu 11: Hệ bất phương trình 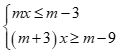 có nghiệm duy nhất khi và chỉ khi
có nghiệm duy nhất khi và chỉ khi
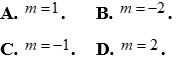
Câu 12: Số -2 thuộc tập nghiệm của bất phương trình nào?
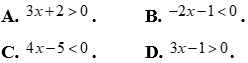
Câu 13: Cho nhị thức bậc nhất 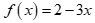 . Trong các mệnh đề sau mệnh đề nào đúng?
. Trong các mệnh đề sau mệnh đề nào đúng?
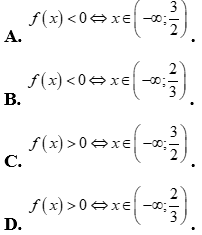
Câu 14: Tập nghiệm của bất phương trình 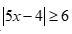 có dạng
có dạng 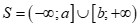 . Tính tổng
. Tính tổng 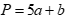 .
.
A. 1. B. 2.
C. 3. D. 4.
Câu 15: Tập nghiệm của bất phương trình 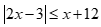
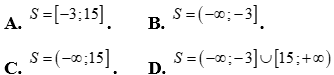
Câu 16: Bất phương trình 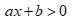 có tập nghiệm là khi và chỉ khi
có tập nghiệm là khi và chỉ khi
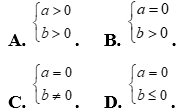
Câu 17: Bất phương trình 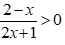 có tập nghiệm là
có tập nghiệm là
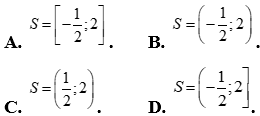
Câu 18: Cho tam thức bậc hai 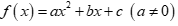 có
có 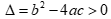 . Gọi
. Gọi 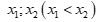 là hai nghiệm phân biệt của
là hai nghiệm phân biệt của ![]() . Chọn mệnh đề đúng trong các mệnh đề sau.
. Chọn mệnh đề đúng trong các mệnh đề sau.
A. ![]() luôn cùng dấu với hệ số a khi
luôn cùng dấu với hệ số a khi 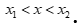 .
.
B. ![]() luôn cùng dấu với hệ số a khi
luôn cùng dấu với hệ số a khi 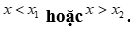
C. ![]() luôn âm với mọi
luôn âm với mọi ![]()
D. ![]() luôn dương với mọi
luôn dương với mọi ![]()
Câu 19: Bảng xét dấu sau là của biểu thức nào?

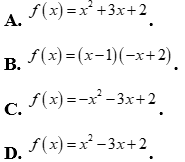
Câu 20: Tìm khẳng định đúng trong các khẳng định sau.
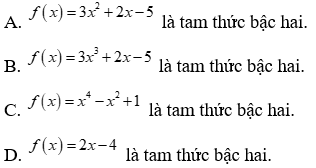
Câu 21: Cho các mệnh đề
(I) với mọi 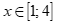 thì
thì 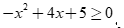 .
.
(II) với mọi 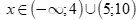 thì
thì 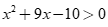 .
.
(III) với mọi 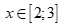 thì
thì 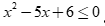 .
.
A. Mệnh đề (I),(III) đúng.
B. Chỉ mệnh đề (I) đúng.
C. Chỉ mệnh đề (III) đúng.
D. Cả ba mệnh đề đều sai.
Câu 22: Bất phương trình có tập nghiệm 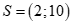 là
là
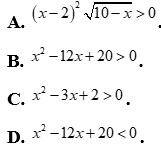
Câu 23: Gọi S là tập nghiệm của bất phương trình 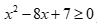 . Trong các tập hợp sau, tập nào không là tập con của S?
. Trong các tập hợp sau, tập nào không là tập con của S?
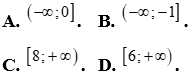
Câu 24: Với x thuộc tập nào dưới đây thì 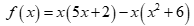 không dương
không dương
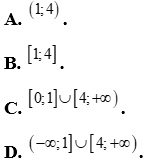
Câu 25: Tổng bình phương các nghiệm nguyên của bất phương trình 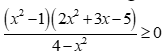 là
là
A. 5. B. 2.
C. 0 . D. 1.
Câu 26: Tập nghiệm của hệ 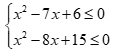
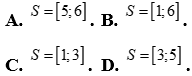
Câu 27: Bất phương trình 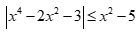 có bao nhiêu nghiệm nguyên?
có bao nhiêu nghiệm nguyên?
A. 0.
B. 1.
C. 2.
D. Nhiều hơn 2 nhưng hữu hạn
Câu 28: Tìm m để mọi 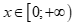 đều là nghiệm của bất phương trình
đều là nghiệm của bất phương trình 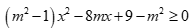
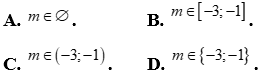
Câu 29: Tìm m để 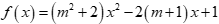 luôn dương với mọi x.
luôn dương với mọi x.
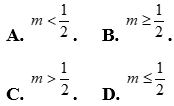
Câu 30: Tập nghiệm của bất phương trình 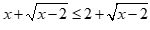 là
là
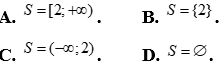
Câu 31: Tập nghiệm của bất phương trình 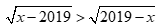 là:
là:
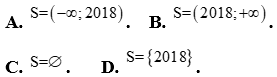
Câu 32: Tính tổng các nghiệm nguyên thuộc ![]() của bất phương trình
của bất phương trình 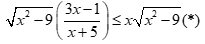
A. 2. B. 12
C. 0. D. 5.
Câu 33: Tập nghiệm của bất phương trình 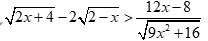 là
là
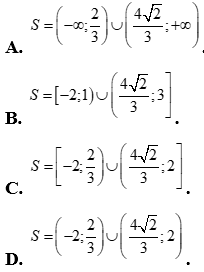
Câu 34: Cho tam giác ABC có 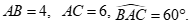 Cạnh BC bằng
Cạnh BC bằng
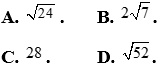
Câu 35: Cho tam giác ABC có 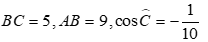 . Tính độ dài đường cao hạ từ đỉnh A của tam giác ABC.
. Tính độ dài đường cao hạ từ đỉnh A của tam giác ABC.
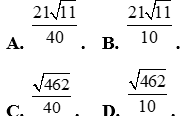
Câu 36: Cho tam giác ABC có 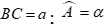 và hai đường trung tuyến
và hai đường trung tuyến 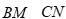 vuông góc với nhau. Diện tích tam giác ABC là:.
vuông góc với nhau. Diện tích tam giác ABC là:.
Câu 37: Cho 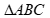 có , bán kính đường tròn ngoại tiếp là . Trong các mệnh đề sau, mệnh đề nào sai?
có , bán kính đường tròn ngoại tiếp là . Trong các mệnh đề sau, mệnh đề nào sai?
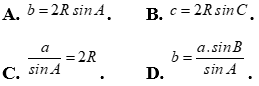
Câu 38: Cho tam giác ABC có 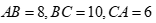 , M là trung điểm của BC. Độ dài trung tuyến AM bằng:
, M là trung điểm của BC. Độ dài trung tuyến AM bằng:
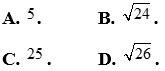
Câu 39: Cho tam giác ABC có 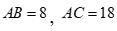 và diện tích bằng 64. Tính
và diện tích bằng 64. Tính 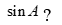 ?
?
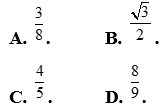
Câu 40: Cho tam giác ABC có 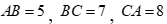 . Bán kính đường tròn nội tiếp tam giác ABC bằng
. Bán kính đường tròn nội tiếp tam giác ABC bằng
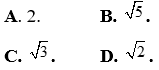
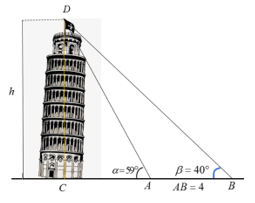
Câu 41: Với các số đo trên hình vẽ sau, chiều cao h của tháp nghiêng Pisa gần với giá trị nào nhất?
Câu 42: Cho đường thẳng ![]() có phương trình
có phương trình 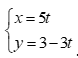 . Trong các điểm sau đây điểm nào không thuộc
. Trong các điểm sau đây điểm nào không thuộc ![]()
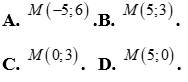
Câu 43: Trong mặt phẳng ![]() , đường thẳng
, đường thẳng 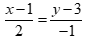 có môt véc tơ chỉ phương là
có môt véc tơ chỉ phương là
A. 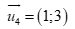 . B.
. B. 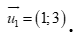 .
.
C. 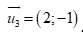 . D.
. D. 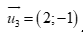 .
.
Câu 44: Cho đường thẳng 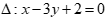 . Vectơ nào sau đây không phải vectơ pháp tuyến của
. Vectơ nào sau đây không phải vectơ pháp tuyến của ![]() ?
?
A. 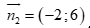 . B.
. B. 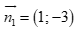 .
.
C. 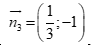 . D.
. D. 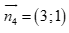 .
.
Câu 45: Phương trình tham số của đường thẳng đi qua hai điểm 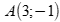 và
và 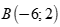 là
là
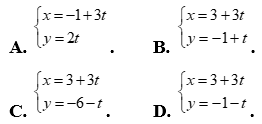
Câu 46: Đường thẳng đi qua M(2,0), song song với đường thẳng 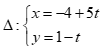 có phương trình tổng quát là
có phương trình tổng quát là
A. 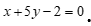 B.
B. 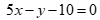 .
.
C. 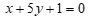 . D.
. D. 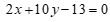 .
.
Câu 47: Cho tam giác ABC có 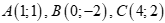 . Phương trình đường trung tuyến AM của tam giác là
. Phương trình đường trung tuyến AM của tam giác là
A. 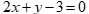 . B.
. B. 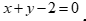 .
.
C. 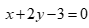 . D.
. D. 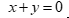 .
.
Câu 48: Cho tam giác ABC có trực tâm H(1,1), phương trình cạnh 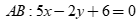 , phương trình cạnh
, phương trình cạnh 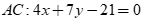 thì phương trình cạnh BC là
thì phương trình cạnh BC là
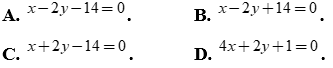
Câu 49: Cho đường thẳng ![]() có phương trình
có phương trình 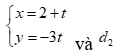 có phương trình
có phương trình 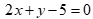 . Biết
. Biết 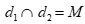 thì tọa độ điểm M là:
thì tọa độ điểm M là:
A. M(-1,-3). B. M(3,1).
C. M(3,-3). D. M(1,3).
Câu 50: Cho 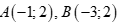 và đường thẳng
và đường thẳng 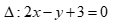 , điểm
, điểm ![]() sao cho tam giác ABC cân ở C. Tọa độ của điểm C là
sao cho tam giác ABC cân ở C. Tọa độ của điểm C là
A. C(0,3). B. C(-2,5).
C. C(-2,-1) . D. C(1,1).
II. Đáp án và thang điểm
A. Bảng đáp án: 0,2 x 50 = 10 điểm
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
C |
A |
A |
C |
C |
C |
D |
D |
D |
B |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
A |
C |
D |
D |
A |
B |
B |
B |
B |
A |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
A |
D |
D |
C |
B |
D |
A |
C |
A |
B |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
B |
C |
C |
B |
B |
D |
A |
A |
D |
C |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
D |
B |
C |
D |
D |
A |
B |
A |
D |
C |
B. Lời giải chi tiết
Câu 1: Tập xác định của hàm số 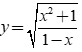 là
là
A. 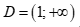 . B.
. B. 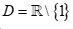 .
.
C. 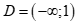 . D.
. D. 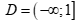 .
.
Lời giải
Chọn C
Hàm số đã cho xác định khi và chỉ khi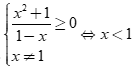 .
.
Vậy tập xác định của hàm số đã cho là 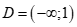 .
.
Câu 2: Phương trình 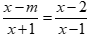 có nghiệm duy nhất khi:
có nghiệm duy nhất khi:
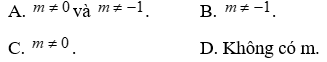
Lời giải
Chọn A
Phương trình xác định khi

Câu 3: Với giá trị nào của m thì phương trình 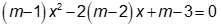 có hai nghiệm
có hai nghiệm 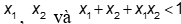 ?
?
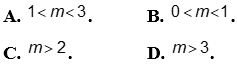
Lời giải
Chọn A
Phương trình có hai nghiệm ![]() khi
khi
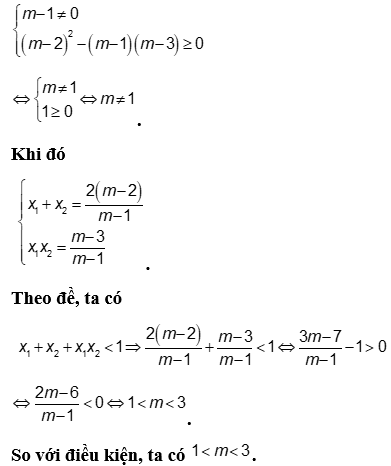
Câu 4: Phương trình 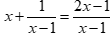 có bao nhiêu nghiệm?
có bao nhiêu nghiệm?
A. 3. B. 2.
C. 1. D. 0.
Lời giải
Chọn C
Điều kiện xác định ![]() .
.
Với điều kiện đó, phương trình đã cho tương đương
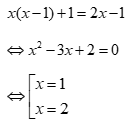
Đối chiếu điều kiện ta có ![]() là nghiệm duy nhất của phương trình.
là nghiệm duy nhất của phương trình.
Vậy phương trình đã cho có 1 nghiệm.
Câu 5: Tập nghiệm của phương trình: 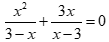 là
là
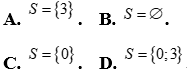
Lời giải
Chọn C
PT
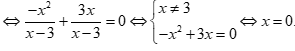
Vậy tập nghiệm phương trình là 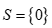 .
.
Câu 6: Phương trình 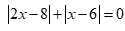 có bao nhiêu nghiệm?
có bao nhiêu nghiệm?
A. 2. B. 1.
C. 0. D. Vô số.
Lời giải
Chọn C

Vậy phương trình (1) vô nghiệm.
Câu 7: Tính tổng các nghiệm của phương trình 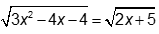
A. 4. B. 3.
C. 5. D. 1.
Lời giải
Chọn D
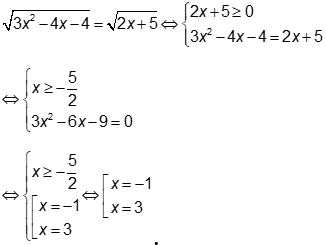
Vậy tổng các nghiệm của phương trình đã cho là: -1+3=2
Câu 8: Tích các nghiệm của phương trình 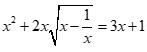 là:
là:
A. 2. B. 3.
C. 0. D. 1.
Lời giải
Chọn D.
Xét phương trình:

nên phương trình này có hai nghiệm phân biệt thỏa mãn điều kiện và có tích là 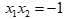 .
.
Câu 9: Chọn khẳng định sai trong các khẳng định sau
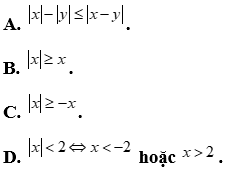
Lời giải
Chọn D
Ta có 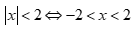 , suy ra khẳng định D sai.
, suy ra khẳng định D sai.
Câu 10: Tìm điều kiện của bất phương trình 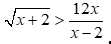 .
.
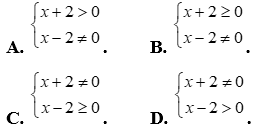
Lời giải
Chọn B
Điều kiện xác định của BPT: 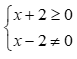 .
.
Câu 11: Hệ bất phương trình 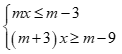 có nghiệm duy nhất khi và chỉ khi
có nghiệm duy nhất khi và chỉ khi
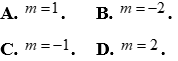
Lời giải
Chọn A
Hệ có nghiệm duy nhất khi và chỉ khi 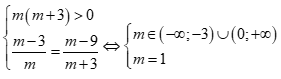 .
.
Câu 12: Số -2 thuộc tập nghiệm của bất phương trình nào?
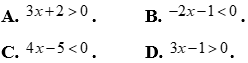
Lời giải
Chọn C
Cách 1: Thay x=-2 lần lượt vào phương án A,B,C,D thì phương án C là đúng.
Cách 2:
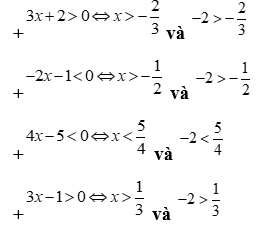
Câu 13: Cho nhị thức bậc nhất 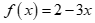 . Trong các mệnh đề sau mệnh đề nào đúng?
. Trong các mệnh đề sau mệnh đề nào đúng?
Lời giải
Chọn D
Nhị thức bậc nhất 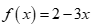 có nghiệm
có nghiệm ![]() và hệ số
và hệ số 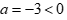 , suy ra
, suy ra 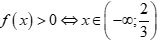 và
và 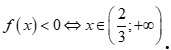 .
.
Câu 14: Tập nghiệm của bất phương trình 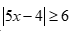 có dạng
có dạng 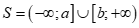 . Tính tổng
. Tính tổng 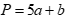 .
.
A. 1. B. 2.
C. 3. D. 4.
Lời giải
Chọn D
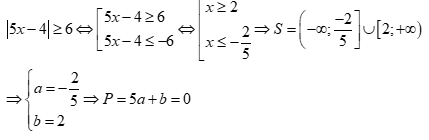
Câu 15: Tập nghiệm của bất phương trình 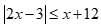
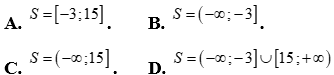
Lời giải
Chọn A
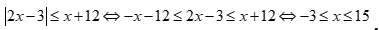 .
.
Vậy 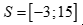 .
.
Câu 16: Bất phương trình 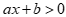 có tập nghiệm là R khi và chỉ khi
có tập nghiệm là R khi và chỉ khi
A. 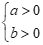 . B.
. B.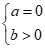 .
.
C. 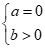 . D.
. D.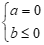 .
.
Lời giải
Chọn B
+ Với 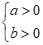 thì
thì 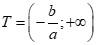 có tập nghiệm
có tập nghiệm 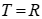 , đáp án A sai.
, đáp án A sai.
+ Với 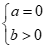 thì
thì 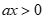 có tập nghiệm
có tập nghiệm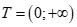 , đáp án B đúng.
, đáp án B đúng.
+ Với 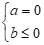 thì
thì 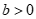 có tập nghiệm , đáp án C sai.
có tập nghiệm , đáp án C sai.
+ Với thì vô nghiệm, đáp án D sai.
Câu 17: Bất phương trình 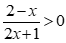 có tập nghiệm là
có tập nghiệm là
A.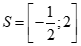 . B.
. B.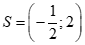 .
.
C. 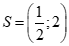 . D.
. D. 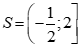 .
.
Lời giải
Chọn B
Ta có dấu của bất phương trình cũng là dấu của bất phương trình 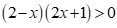
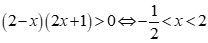
Vậy tập nghiệm của bất phương trình đã cho là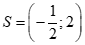 .
.
Câu 18: Cho tam thức bậc hai 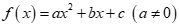 có
có 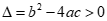 . Gọi
. Gọi 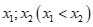 là hai nghiệm phân biệt của
là hai nghiệm phân biệt của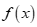 . Chọn mệnh đề đúng trong các mệnh đề sau.
. Chọn mệnh đề đúng trong các mệnh đề sau.
A. 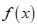 luôn cùng dấu với hệ số a khi
luôn cùng dấu với hệ số a khi 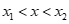 .
.
B. 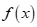 luôn cùng dấu với hệ số a khi
luôn cùng dấu với hệ số a khi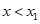 hoặc
hoặc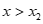 .
.
C. 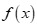 luôn âm với mọi
luôn âm với mọi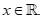
D. 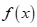 luôn dương với mọi
luôn dương với mọi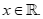
Lời giải
Chọn B
Theo định lí về dấu của tam thức bậc hai.
Câu 19: Bảng xét dấu sau là của biểu thức nào?

A.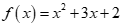 . B.
. B.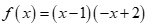 .
.
C.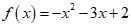 . D.
. D.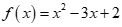 .
.
Lời giải
Chọn B
Câu 20: Tìm khẳng định đúng trong các khẳng định sau.
A. 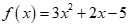 là tam thức bậc hai.
là tam thức bậc hai.
B. 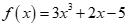 là tam thức bậc hai.
là tam thức bậc hai.
C.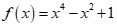 là tam thức bậc hai.
là tam thức bậc hai.
D. 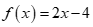 là tam thức bậc hai.
là tam thức bậc hai.
Lời giải
Chọn A
Câu 21: Cho các mệnh đề
(I)với mọi 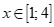 thì
thì 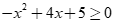 .
.
(II) với mọi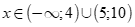 thì
thì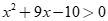 .
.
(III) với mọi 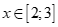 thì
thì 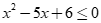 .
.
A. Mệnh đề (I) ,(III) đúng. B. Chỉ mệnh đề (I) đúng.
C. Chỉ mệnh đề (III) đúng. D. Cả ba mệnh đề đều sai.
Lời giải
Chọn A
Ta có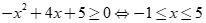 . Vậy (I)đúng.
. Vậy (I)đúng.
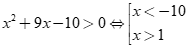 . Vậy sai.
. Vậy sai.
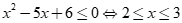 . Vậy đúng.
. Vậy đúng.
Câu 22: Bất phương trình có tập nghiệm là
A.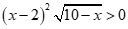 . B.
. B. 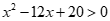 .
.
C.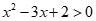 . D.
. D.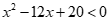 .
.
Lời giải
Chọn D
Xét đáp án A: 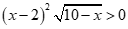
Ta thấy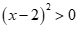 ,
, 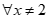 và
và 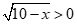 với mọi
với mọi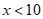 .
.
Tập nghiệm của bất phương trình là 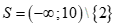 .
.
Xét đáp án B: 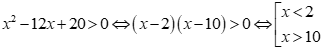
Tập nghiệm của bất phương trình là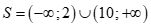 .
.
Xét đáp án C: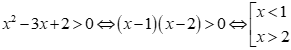
Tập nghiệm của bất phương trình là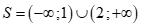 .
.
Xét đáp án D: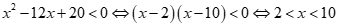 .
.
Tập nghiệm của bất phương trình là 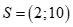
Câu 23: Gọi S là tập nghiệm của bất phương trình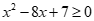 . Trong các tập hợp sau, tập nào không là tập con của ?
. Trong các tập hợp sau, tập nào không là tập con của ?
A.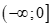 . B.
. B.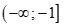 .
.
C.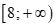 . D.
. D. 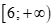 .
.
Lời giải
Chọn D
.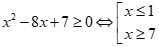
Suy ra 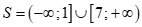 . Do đó
. Do đó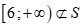 .
.
Câu 24: Với x thuộc tập nào dưới đây thì 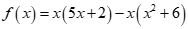 không dương
không dương
A. 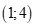 . B.
. B.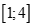 .
.
C.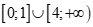 . D.
. D.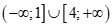 .
.
Lời giải
Chọn C.

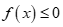
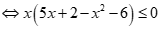
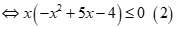
Có 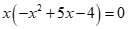
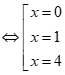
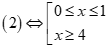
Vậy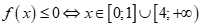 .
.
Câu 25: Tổng bình phương các nghiệm nguyên của bất phương trình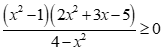 là
là
A. 5. B. 2. C.0 . D.1 .
Lời giải
Chọn B
Ta có:
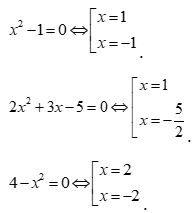
Trục xét dấu:
Tập nghiệm của bất phương trình là 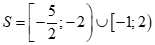
Tổng bình phương các nghiệm nguyên bất phương trình là: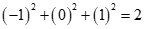 .
.
Câu 26: Tập nghiệm của hệ 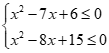
A. 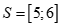 . B.
. B. 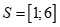 . C.
. C.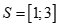 . D.
. D.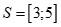 .
.
Lời giải
Chọn D
Ta có .
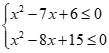
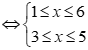
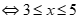
Câu 27: Bất phương trình 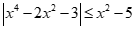 có bao nhiêu nghiệm nguyên?
có bao nhiêu nghiệm nguyên?
A. 0. B.1 .
C.2 . D. Nhiều hơn 2 nhưng hữu hạn
Lời giải
Chọn A
Đặt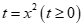 .
.
Khi đó bất phương trình trở thành 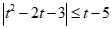
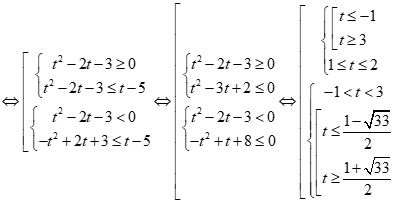
Vô nghiệm.
Vậy bất phương trình đã cho vô nghiệm.
Câu 28: Tìm m để mọi 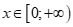 đều là nghiệm của bất phương trình
đều là nghiệm của bất phương trình 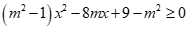
A. 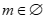 . B.
. B.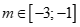 .
.
C.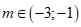 . D.
. D.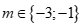 .
.
Lời giải
Chọn C
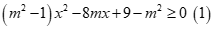
+)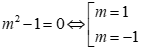
Với m=1 bất phương trình có dạng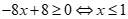 . Do đó m=1 không thoả mãn.
. Do đó m=1 không thoả mãn.
Với m=-1 bất phương trình có dạng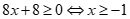 . Do đó m=-1 là một giá trị cần tìm.
. Do đó m=-1 là một giá trị cần tìm.
+) 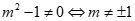 . Khi đó vế trái là tam thức bậc hai có
. Khi đó vế trái là tam thức bậc hai có 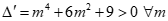 nên
nên
tam thức luôn có 2 nghiệm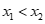 .
.
Suy ra mọi 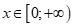 đều là nghiệm của bất phương trình
đều là nghiệm của bất phương trình 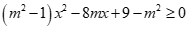 khi và chỉ khi
khi và chỉ khi
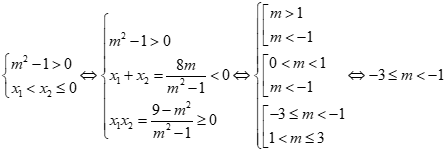
Từ đó suy ra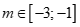 .
.
Câu 29: Tìm m để 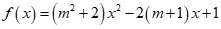 luôn dương với mọi x.
luôn dương với mọi x.
A.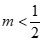 . B.
. B.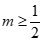 . C.
. C.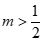 . D.
. D.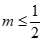 .
.
Lời giải
Chọn A
Nhận thấy 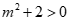 với mọi m nên
với mọi m nên 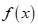 là một tam thức bậc 2.
là một tam thức bậc 2.
Để 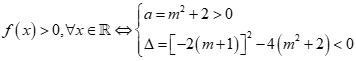 .
.
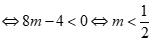
Câu 30: Tập nghiệm của bất phương trình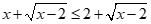 là
là
A.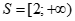 . B.
. B.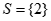 .
.
C.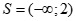 . D.
. D.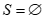 .
.
Lời giải
Chọn B
Ta có: 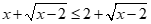
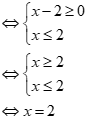
Vậy tập nghiệm của bất phương trình là: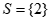 .
.
Câu 31: Tập nghiệm của bất phương trình 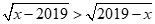 là:
là:
A.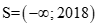 . B.
. B.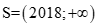 .
.
C.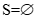 . D.
. D.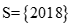 .
.
Lời giải
Chọn B
Điều kiện:
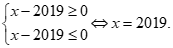
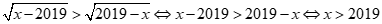
không thỏa điều kiện.
Vậy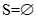 .
.
Câu 32: Tính tổng các nghiệm nguyên thuộc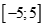 của bất phương trình
của bất phương trình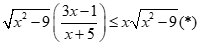
A. 2. B.12
C. 0. D. 5.
Lời giải
Chọn C
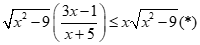
Điều kiện:
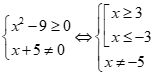 .
.
- Nếu 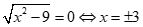 , bất phương trình đúng.
, bất phương trình đúng.
- Nếu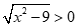
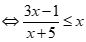 ,
,
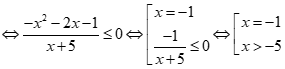
Mà 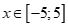 .
.
Nên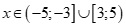 .
.
Do đó tổng tất cả các nghiệm nguyên thuộc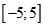 của bất phương trình là:
của bất phương trình là: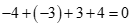 .
.
Câu 33: Tập nghiệm của bất phương trình 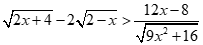 là
là
A.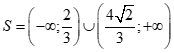 .
.
B. 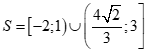 .
.
C. 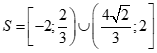 . D.
. D.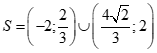 .
.
Lời giải
Chọn C
Bất phương trình: 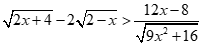 .
.
Điều kiện: 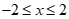 .
.
Bất phương trình tương đương: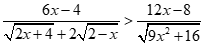 .
.
+ Với 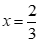 không thỏa mãn.
không thỏa mãn.
+ Với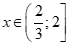 , ta có:
, ta có:
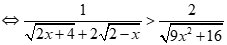
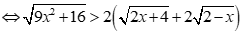
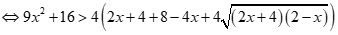
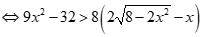
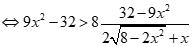
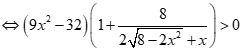
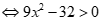
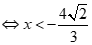
hoặc .
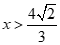
Suy ra 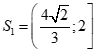 .
.
+ Với 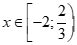 , ta có:(*)
, ta có:(*) 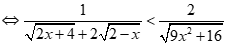
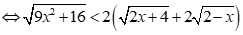 , đúng với
, đúng với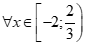
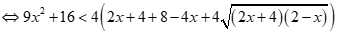
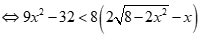
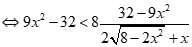
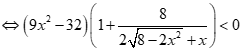
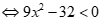
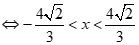
Suy ra 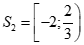 .
.
Vậy bất phương trình có tập nghiệm 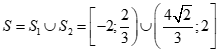 .
.
Câu 34: Cho tam giác có Cạnh bằng
A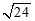 . . B.
. . B.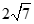
C.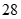 . D.
. D. 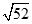 .
.
Lời giải
Chọn B
Áp dụng định lý cosin cho tam giác ABC, ta có:
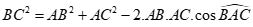
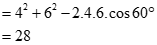
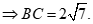
Câu 35: Cho tam giácABC có 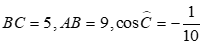 . Tính độ dài đường cao hạ từ đỉnh A của tam giác ABC .
. Tính độ dài đường cao hạ từ đỉnh A của tam giác ABC .
A.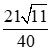 . B.
. B.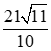 .
.
C.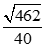 . D.
. D. 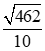 .
.
Lời giải
Chọn B
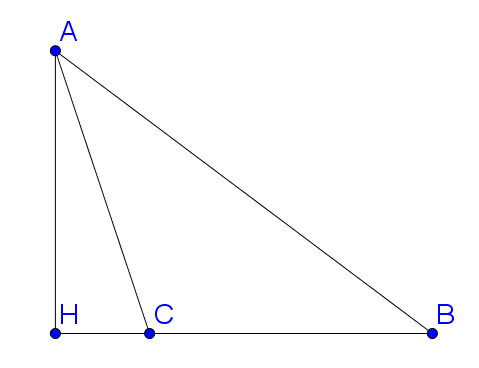
Do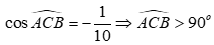 .
.
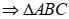 như hình vẽ.
như hình vẽ.
Áp dụng hệ quả ĐL cosin cho tam giác ABC ta có:
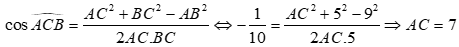 .
.
Khi đó:
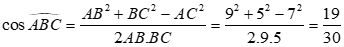 .
.
Mà
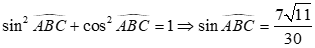 .
.
Xét tam giác AHB vuông tại H, ta có:
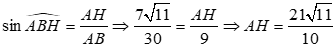 .
.
Câu 36: Cho tam giác ABC có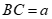 ;
; 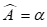 và hai đường trung tuyến BM ,CN vuông góc với nhau. Diện tích tam giác ABC là:.
và hai đường trung tuyến BM ,CN vuông góc với nhau. Diện tích tam giác ABC là:.
A.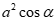 . B.
. B. 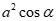 .
.
C. 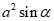 . D.
. D.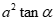 .
.
Lời giải
Chọn D
Trong tam giác ABC với 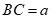 ;
; 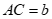 ,
,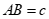 .
.
Tam giác ABC có hai đường trung tuyến BM,CN vuông góc với nhau khi và chỉ khi 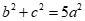 .
.
Mặt khác theo định lí cô sin trong tam giác, ta có .
Từ (1)và (2) suy ra
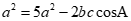
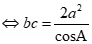 .
.
Diện tích tam giác
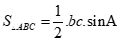 .
.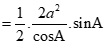
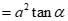
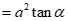
Chứng minh bài toán: Tam giác ABC có hai đường trung tuyến BM ,CN vuông góc với nhau khi và chỉ khi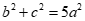 .
.
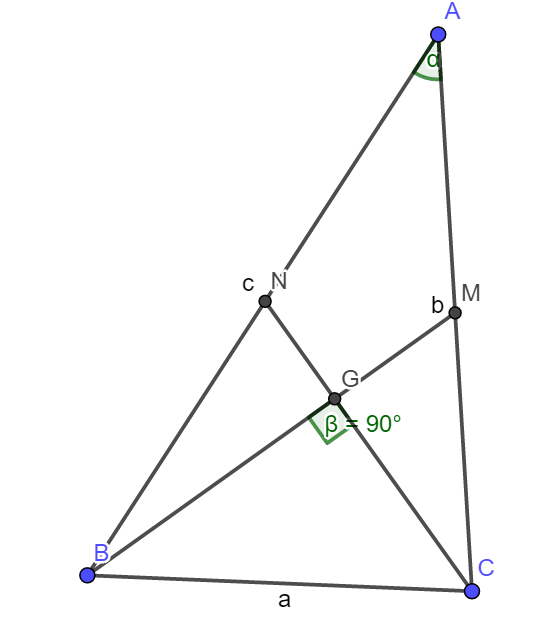
Ta có: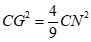 .
.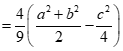
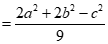
Tương tự, ta có 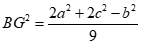 .
.
Do 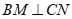
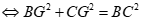
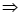
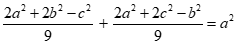
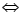
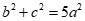
Câu 37: Cho 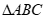 có
có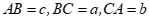 , bán kính đường tròn ngoại tiếp là . Trong các mệnh đề sau, mệnh đề nào sai?
, bán kính đường tròn ngoại tiếp là . Trong các mệnh đề sau, mệnh đề nào sai?
A.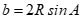 . B.
. B.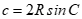 .
.
C.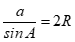 . D.
. D. 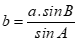 .
.
Lời giải
Chọn A
Theo định lý sin ta có: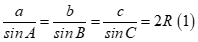 .
.
Từ công thức 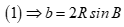 nên phương án A sai.
nên phương án A sai.
Từ công thức 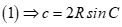 nên phương án B đúng.
nên phương án B đúng.
Từ công thức 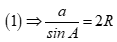 nên phương án C đúng.
nên phương án C đúng.
Từ công thức 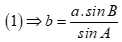 nên phương án D đúng.
nên phương án D đúng.
Câu 38: Cho tam giác ABC có 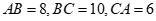 , M là trung điểm của BC. Độ dài trung tuyến AM bằng:
, M là trung điểm của BC. Độ dài trung tuyến AM bằng:
A.5 . B.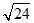 .
.
C.25 . D.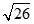 .
.
Lời giải
Chọn A
Trong tam giác ABC ta có, 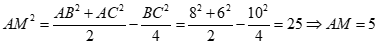 .
.
Câu 39: Cho tam giác ABC có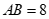 ,
, 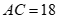 và diện tích bằng 64. Tính SinA ?
và diện tích bằng 64. Tính SinA ?
A.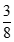 . B.
. B.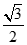 .
.
C.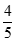 . D.
. D. 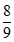 .
.
Lời giải
Chọn D
Áp dụng công thức tính diện tích ![]() :
: 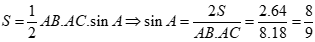 .
.
Câu 40: Cho tam giác ABC có 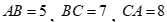 . Bán kính đường tròn nội tiếp tam giác ABC bằng
. Bán kính đường tròn nội tiếp tam giác ABC bằng
A. 2. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
Lời giải
Chọn C
Đặt 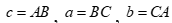 ,
, 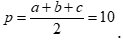 .
.
Diện tích tam giác ABC bằng 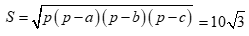 .
.
Bán kính đường tròn nội tiếp ![]()
![]()
![]() .
.
Câu 41: Với các số đo trên hình vẽ sau, chiều cao của tháp nghiêng Pisa gần với giá trị nào nhất?
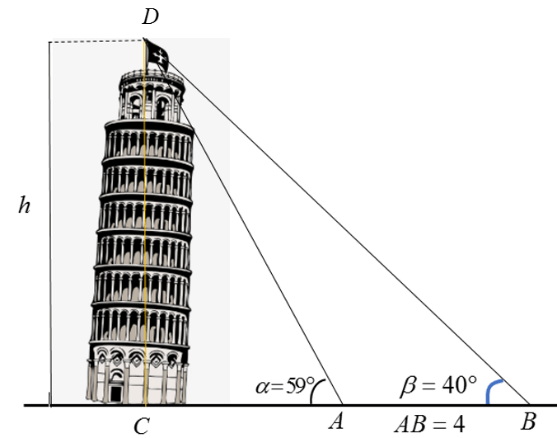
A.8. B. 7.5.
C. 6.5. D.7.
Lời giải
Chọn D
Xét tam giác ABC ta có: 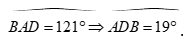 .
.
Lại có: 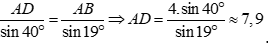
Xét tam giác CAD vuông tại C có: 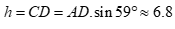 .
.
Câu 42: Cho đường thẳng ![]() có phương trình
có phương trình 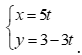 . Trong các điểm sau đây điểm nào không thuộc
. Trong các điểm sau đây điểm nào không thuộc ![]()
A. 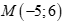 . B.
. B. 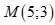 .
.
C. 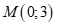 . D.
. D. 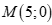 .
.
Lời giải
Chọn B
Với 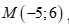 thay
thay 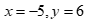 vào phương trình
vào phương trình 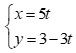 ta có:
ta có:
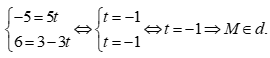
Với 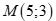 thay
thay 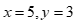 vào phương trình
vào phương trình 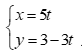 ta có:
ta có:
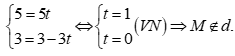
Với 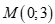 thay
thay 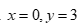 vào phương trình
vào phương trình 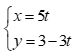 ta có:
ta có:
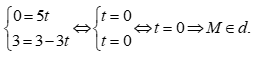
Với 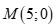 thay
thay 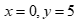 vào phương trình
vào phương trình 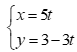 ta có:
ta có:
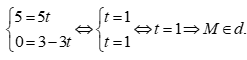
Câu 43: Trong mặt phẳng Oxy, đường thẳng 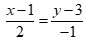 có môt véc tơ chỉ phương là
có môt véc tơ chỉ phương là
A. 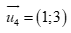 . B.
. B. 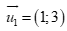
C. 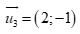 . D.
. D. 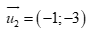 .
.
Lời giải
Chọn C
Đường thẳng 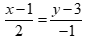 có một véc tơ chỉ phương là
có một véc tơ chỉ phương là 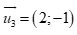 .
.
Câu 44: Cho đường thẳng 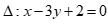 . Vectơ nào sau đây không phải vectơ pháp tuyến của
. Vectơ nào sau đây không phải vectơ pháp tuyến của ![]() ?
?
A. 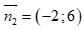 . B.
. B. 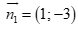 . C.
. C. 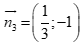 . D.
. D. 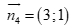 .
.
Lời giải
Chọn D
Ta có, vectơ pháp tuyến của ![]() có dạng
có dạng 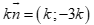 với K khác 0.
với K khác 0.
Đối chiếu các đáp án suy ra D sai.
Câu 45: Phương trình tham số của đường thẳng đi qua hai điểm A(3,-1) và B(-6,2) là
A. 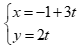 . B.
. B. 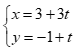 .
.
C. 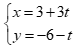 . D.
. D. 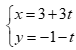 .
.
Lời giải
Chọn D
Đường thẳng AB đi qua hai điểm 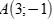 và
và 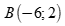 nên đường thẳng AB nhận
nên đường thẳng AB nhận 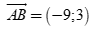 làm véc tơ chỉ phương hay nhận
làm véc tơ chỉ phương hay nhận 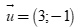 làm véc tơ chỉ phương.
làm véc tơ chỉ phương.
Vậy đường thẳng AB đi qua 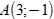 và nhận
và nhận 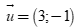 làm véc tơ chỉ phương có phương trình tham số là
làm véc tơ chỉ phương có phương trình tham số là 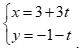 .
.
Câu 46: Đường thẳng đi qua M(2,0), song song với đường thẳng 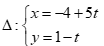 có phương trình tổng quát là
có phương trình tổng quát là
A. 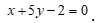 . B.
. B. 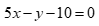 .
.
C. 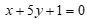 . D.
. D. 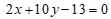 .
.
Lời giải
Chọn A
Gọi d là đường thẳng đi qua M(2,0) và song song với đường thẳng ![]() .
.
Đường thẳng ![]() có VTCP
có VTCP 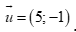 , thì đường thẳng d có VTCP
, thì đường thẳng d có VTCP 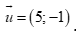 .
.
Suy ra đường thẳng d có VTPT 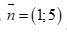 .
.
Phương trình tổng quát của đường thẳng d đi qua M(2,0), VTPT 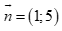 có dạng:
có dạng:
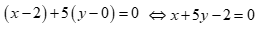 .
.
Câu 47: Cho tam giác ABC có 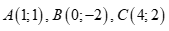 . Phương trình đường trung tuyến AM của tam giác là
. Phương trình đường trung tuyến AM của tam giác là
A. 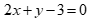 . B.
. B. 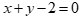 . C.
. C. 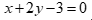 . D.
. D. 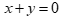 .
.
Lời giải
Chọn B
Gọi M là trung điểm của cạnh 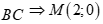 .
.
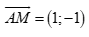 .
.
Đường thẳng đi qua điểm ![]() nhận
nhận 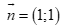 làm một vectơ pháp tuyến có phương trình là:
làm một vectơ pháp tuyến có phương trình là:
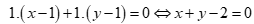 .
.
Câu 48: Cho tam giác ABC có trực tâm H(1,1), phương trình cạnh 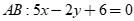 , phương trình cạnh
, phương trình cạnh 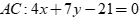 thì phương trình cạnh BC là
thì phương trình cạnh BC là
A. 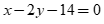 . B.
. B. 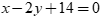 .
.
C. 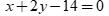 . D.
. D. 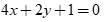 .
.
Lời giải
Chọn A
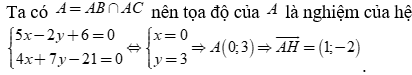
Ta có đường thẳng 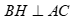 nên phương trình đường thẳng
nên phương trình đường thẳng 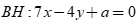 .
.
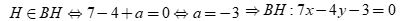 .
.
Ta có 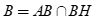 nên tọa độ của  là nghiệm của hệ
nên tọa độ của  là nghiệm của hệ 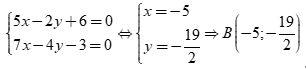 .
.
Đường thẳng BC đi qua điểm B nhận ![]() là VTPT có phương trình
là VTPT có phương trình 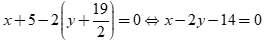 .
.
Câu 49: Cho đường thẳng d1 có phương trình 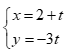 và d2 có phương trình
và d2 có phương trình 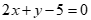 . Biết
. Biết 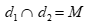 thì tọa độ điểm M là:
thì tọa độ điểm M là:
A. 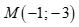 . B.
. B. 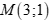 .
.
C. 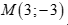 . D.
. D. 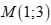 .
.
Lời giải
Chọn D
Do 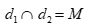 nên tọa độ điểm M là nghiệm của hệ phương trình:
nên tọa độ điểm M là nghiệm của hệ phương trình:
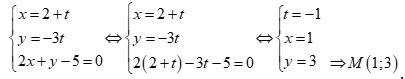
Câu 50: Cho 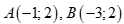 và đường thẳng
và đường thẳng 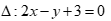 , điểm
, điểm ![]() sao cho tam giác ABC cân ở C. Tọa độ của điểm C là
sao cho tam giác ABC cân ở C. Tọa độ của điểm C là
A. C(0,3). B. C(-2,5). C. C(-2,-1). D. C(1,1).
Lời giải
Chọn C
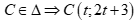 .
.
Do tam giác ABC cân ở C nên 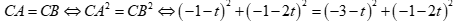
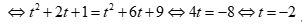 .
.
Suy ra C(-2,-1).

Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Năm học 2023
Môn: Ngữ Văn 10
Thời gian làm bài: 90 phút
(Đề số 5)
I. Trắc nghiệm (7 điểm)
Câu 1: Tam thức bậc hai 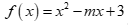 . Với giá trị nào của m thì f(x) có hai nghiệm phân biệt?
. Với giá trị nào của m thì f(x) có hai nghiệm phân biệt?
A. 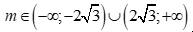 .
.
B. 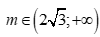 .
.
C. 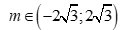
.D. 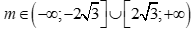 .
.
Câu 2: Tìm tất cả các giá trị thỏa mãn điều kiện của bất phương trình 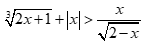 .
.
A. 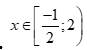 B.
B. 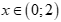
C. 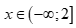 D.
D. 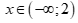
Câu 3: Cặp bất phương trình nào sau đây là tương đương?
A. 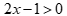 và
và 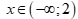
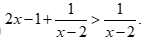
B. 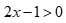 và
và 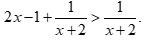
C. 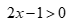 và
và 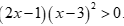
D. 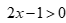 và
và 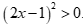
Câu 4: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
A. 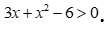 . B.
. B. 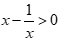 .
.
C. ![]() . D.
. D. 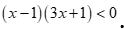 .
.
Câu 5: Hệ bất phương trình sau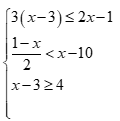 có tập nghiệm là
có tập nghiệm là
A. ![]() . B.
. B. 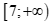 .
.
C. ![]() D.
D. ![]() .
.
Câu 6: Bảng xét dấu sau là của biểu thức nào?

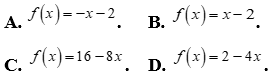
Câu 7: Tập nghiệm của phương trình -3x -6 > 0 là:

Câu 8: 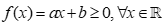 khi và chỉ khi
khi và chỉ khi
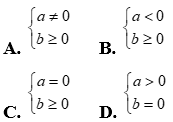
Câu 9: Tìm số các giá trị nguyên của m để mọi x thuộc đoạn 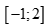 đều là nghiệm của bất phương trình
đều là nghiệm của bất phương trình 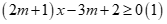
A. 6. B. 4.
C. 5. D. 3
Câu 10: Miền nghiệm của bất phương trình 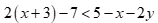 không chứa điểm nào trong các điểm sau?
không chứa điểm nào trong các điểm sau?
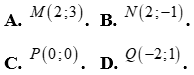
Câu 11: Cho hệ bất phương trình 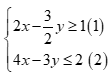 có tập nghiệm là s. Mệnh đề nào sau đây là đúng?
có tập nghiệm là s. Mệnh đề nào sau đây là đúng?
A. Biểu diễn hình học của s là nửa mặt phẳng chứa gốc tọa độ kể cả bờ d, với d là đường thẳng 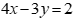 .
.
B. Biểu diễn hình học của s là nửa mặt phẳng không chứa gốc tọa độ kể cả bờ d, với d là đường thẳng 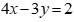 .
.
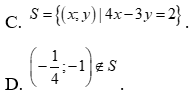
Câu 12: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ sau?
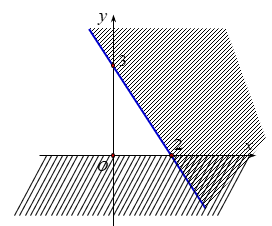
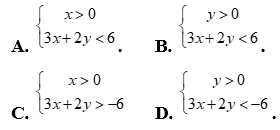
Câu 13: Một người nông dân dự định trồng mía và ngô trên diện tích 8 sào đất (1 sào bằng 360m2). Nếu trồng mía thì trên mỗi sào cần 10công và thu lãi 1500000 đồng, nếu trồng ngô thì trên mỗi sào cần công và thu lãi 2000000 đồng. Biết tổng số công cần dùng không vượt quá 90công. Tính tổng số tiền lãi cao nhất mà người nông dân có thể thu được.
A. 14 (triệu đồng) B. 12 (triệu đồng)
C. 16 (triệu đồng) D. 13 (triệu đồng)
Câu 14: Tập nghiệm của bất phương trình 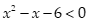 là:
là:
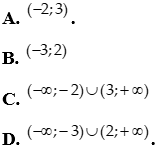
Câu 15: Tam thức bậc hai 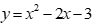 nhận giá trị dương khi và chỉ khi
nhận giá trị dương khi và chỉ khi
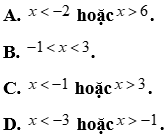
Câu 16: Tập nghiệm của bất phương trình: 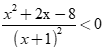 là:
là:
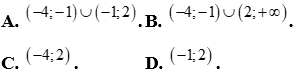
Câu 17: Gọi M,m lần lượt là nghiệm nguyên lớn nhất và nhỏ nhất của bất phương trình 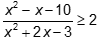 . Tính M+m.
. Tính M+m.
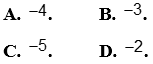
Câu 18: Hệ bất phương trình 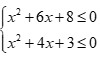 có tất cả bao nhiêu nghiệm nguyên?
có tất cả bao nhiêu nghiệm nguyên?
A. 5. B. 1.
C. 2. D. 0.
Câu 19: Cho hệ bất phương trình 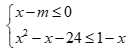 . Hệ đã cho có nghiệm khi và chỉ khi
. Hệ đã cho có nghiệm khi và chỉ khi
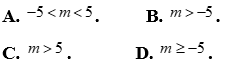
Câu 20: Bất phương trình 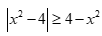 có tập nghiệm là:
có tập nghiệm là:
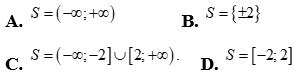
Câu 21: Cho tam thức bậc hai 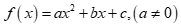 . Điều kiện cần và đủ để
. Điều kiện cần và đủ để 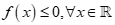 là:
là:
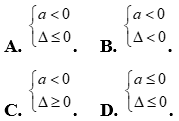
Câu 22: Cho tam thức bậc hai 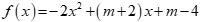 . Tìm m để f(x) luôn âm với mọi
. Tìm m để f(x) luôn âm với mọi 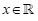 .
.
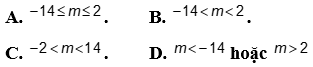
Câu 23: Bất phương trình 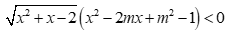 có nghiệm khi và chỉ khi
có nghiệm khi và chỉ khi 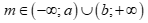 . Tính
. Tính 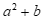 .
.
A. 5. B. 1.
C. 2. D. 0.
Câu 24: Tập nghiệm của bất phương trình 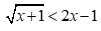 là :
là :
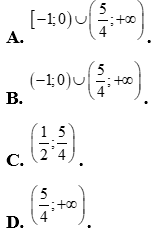
Câu 25: Tam giác ABC có 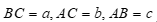 , góc
, góc 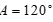 . Mệnh đề nào sau đây là đúng ?
. Mệnh đề nào sau đây là đúng ?
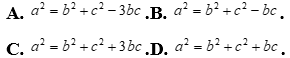
Câu 26: Cho 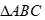 có
có 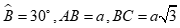 , trên cạnh BC lấy điểm M sao cho
, trên cạnh BC lấy điểm M sao cho 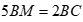 .
.
Tính độ dài đoạn .
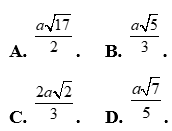
Câu 27: Cho tam giác ABC có 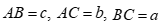 . Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Mệnh đề nào sau đây đúng?
. Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Mệnh đề nào sau đây đúng?
A. 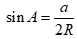 . B.
. B. 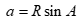 .
.
C.  . D.
. D.  .
.
Câu 28: Muốn đo khoảng cách từ người A trên bờ đến chiếc thuyền C neo đậu trên sông, người ta chọn một điểm B trên bờ và đo đượCab=160m, .Tính độ dài đoạn (xấp xỉ đến hàng phần trăm)
A. 74,87 (m) B. 74,88 (m)
C. 165,93 (m) D. 165,89 (m)
Câu 29: Cho tam giác ABC có  . Gọi M là trung điểm của BC. Mệnh đề nào sau đây đúng?
. Gọi M là trung điểm của BC. Mệnh đề nào sau đây đúng?
A.  .
.
B. 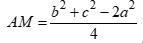 .
.
C. 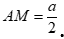 .
.
D. 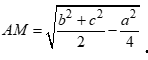 .
.
Câu 30: Cho một tam giác có độ dài ba cạnh lần lượt là 13,14,15. Tính bán kính đường tròn nội tiếp tam giác đó.
A. 2. B. 4.
C. ![]() . D. 3.
. D. 3.
Câu 31: Cho tam giác ABC có BC=a, góc A bằng ![]() và hai đường trung tuyến BM,CN vuông góc với nhau. Diện tích tam giác ABC là
và hai đường trung tuyến BM,CN vuông góc với nhau. Diện tích tam giác ABC là
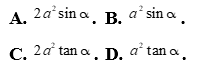
Câu 32: Cho tam giác ABC có 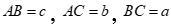 . Nhận dạng tam giác ABC biết
. Nhận dạng tam giác ABC biết 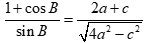 .
.
A. Tam giác cân. B. Tam giác vuông.
C. Tam giác đều. D. Tam giác có góc 60 độ.
Câu 33: Tam giác ABC có 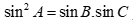 . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
A. 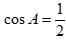 . B.
. B. 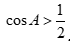 .
.
C. 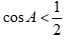 . D.
. D. 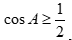 .
.
Câu 34: Trong các cặp bất phương trình dưới đây, cặp bất phương trình nào tương đương?
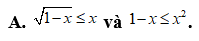
B. ![]() và
và ![]() .
.
C. 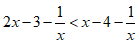 và
và 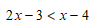 .
.
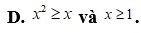
Câu 35: Bất phương trình 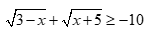 có bao nhiêu nghiệm?
có bao nhiêu nghiệm?
A. Hai nghiệm. B. Vô số nghiệm.
C. Vô nghiệm. D. Có một nghiệm.
II. Tự luận (3 điểm)
Câu 36. Giải bất phương trình 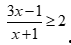 .
.
Câu 37. Tìm m để 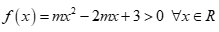 .
.
Câu 38. Cho tam giác ABC có 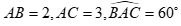 . Tính độ dài BC và .
. Tính độ dài BC và .
Đáp án và thang điểm
I. Trắc nghiệm
A. Bảng đáp án: 0,2 x 35 = 7 điểm
1 |
2 |
3 |
4 |
5 |
6 |
7 |
A |
D |
B |
C |
C |
C |
D |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
C |
C |
D |
C |
B |
D |
A |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
C |
A |
A |
C |
D |
A |
A |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
B |
B |
D |
A |
D |
A |
D |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
D |
B |
D |
A |
D |
C |
B |
B. Lời giải chi tiết
Câu 1: Tam thức bậc hai 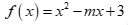 . Với giá trị nào của m thì f(x) có hai nghiệm phân biệt?
. Với giá trị nào của m thì f(x) có hai nghiệm phân biệt?
A. 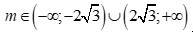 .
.
B. 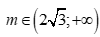 .
.
C. 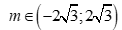
.D. 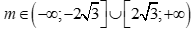 .
.
Lời giải
Chọn A
Để f(x) có hai nghiệm phân biệt thì 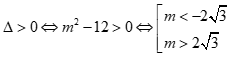
Lời giải
Chọn A
Để f(x) có hai nghiệm phân biệt thì 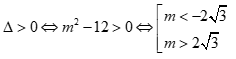
Câu 3: Cặp bất phương trình nào sau đây là tương đương?
A. 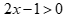 và
và 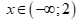
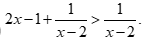
B. 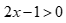 và
và 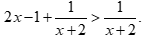
C. 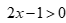 và
và 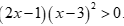
D. 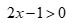 và
và 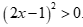
Lời giải
Chọn B
Bất phương trình 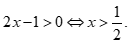
Bất phương trình 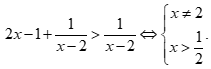 Đáp án A sai.
Đáp án A sai.
Bất phương trình 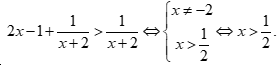 Đáp án B đúng.
Đáp án B đúng.
Bất phương trình 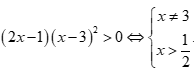 Đáp án C sai.
Đáp án C sai.
Bất phương trình 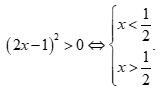 Đáp án D sai.
Đáp án D sai.
Ghi nhớ: Hai bất phương trình (cùng ẩn) được gọi là tương đương nếu chúng có cùng tập nghiệm.
Câu 4: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
A. 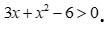 . B.
. B. 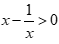 .
.
C. ![]() . D.
. D. 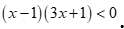 .
.
Lời giải
Chọn C
Ghi nhớ:Bất phương trình bậc nhất một ẩn x có dạng tổng quát là:
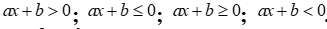 . Trong đó, a,b là các hằng số,
. Trong đó, a,b là các hằng số, ![]() và x là ẩn số.
và x là ẩn số.
Câu 5: Hệ bất phương trình sau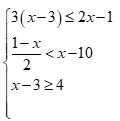 có tập nghiệm là
có tập nghiệm là
A. ![]() . B.
. B. 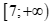 .
.
C. ![]() D.
D. ![]() .
.
Lời giải
Chọn C
Ta có
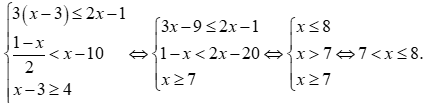
Vậy tập nghiệm của hệ bất phương trình .
Câu 6: Bảng xét dấu sau là của biểu thức nào?

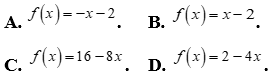
Lời giải
Chọn C
* Ta có:
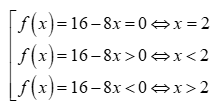
* Hoặc nhận dạng bảng xét dấu của nhị thức bậc nhất “phải cùng trái khác với a”.
Câu 7: Tập nghiệm của phương trình -3x -6 > 0 là:

Lời giải
Chọn D
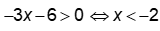
Vậy tập nghiệm của bất phương trình là 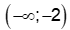 .
.
Câu 8: 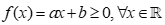 khi và chỉ khi
khi và chỉ khi
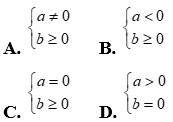
Lời giải
Chọn C
* Với a>0 ta có: 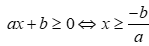 (không thỏa mãn yêu cầu bài toán là
(không thỏa mãn yêu cầu bài toán là 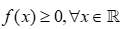 )
)
* Với a<0 ta có: 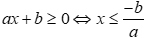 (không thỏa mãn yêu cầu bài toán là
(không thỏa mãn yêu cầu bài toán là 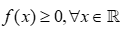 )
)
* Với a=0 ta có 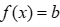 khi đó
khi đó 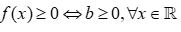
Vậy 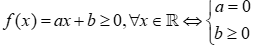
Câu 9:
Tìm số các giá trị nguyên của m để mọi x thuộc đoạn 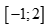 đều là nghiệm của bất phương trình
đều là nghiệm của bất phương trình 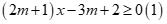
A. 6. B. 4.
C. 5. D. 3
Lời giải
Chọn C.
*) Nếu 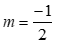 ta được bất phương trình (1) trở thành
ta được bất phương trình (1) trở thành 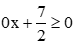 , bất phương trình này đúng với mọi x thuộc
, bất phương trình này đúng với mọi x thuộc ![]()
*) Nếu 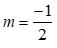 ta được bất phương trình (1) có tập nghiệm
ta được bất phương trình (1) có tập nghiệm 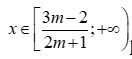 khi đó yêu cầu bài toán xảy ra khi
khi đó yêu cầu bài toán xảy ra khi 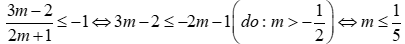
. Kết hợp với 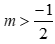 nên
nên 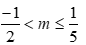
*) Nếu 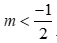 ta được bất phương trình (1)có tập nghiệm
ta được bất phương trình (1)có tập nghiệm 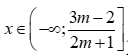
khi đó yêu cầu bài toán xảy ra khi
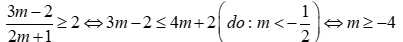
. Kết hợp với 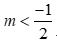 nên
nên 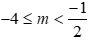
Kết hợp cả 3 trường hợp ta có: m thuộc đoạn 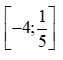 sẽ thỏa mãn. Do m nguyên nên
sẽ thỏa mãn. Do m nguyên nên 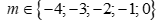
Có 5 giá rị nguyên của m thỏa mãn.
Câu 10:
Miền nghiệm của bất phương trình 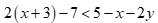 không chứa điểm nào trong các điểm sau?
không chứa điểm nào trong các điểm sau?
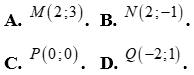
Lời giải
Chọn D
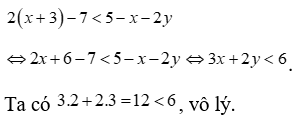
Vậy miền nghiệm của bất phương trình 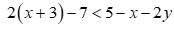 không chứa điểm
không chứa điểm 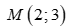 .
.
Câu 11:
Cho hệ bất phương trình 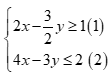 có tập nghiệm là s. Mệnh đề nào sau đây là đúng?
có tập nghiệm là s. Mệnh đề nào sau đây là đúng?
A. Biểu diễn hình học của s là nửa mặt phẳng chứa gốc tọa độ kể cả bờ d, với d là đường thẳng 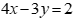 .
.
B. Biểu diễn hình học của s là nửa mặt phẳng không chứa gốc tọa độ kể cả bờ d, với d là đường thẳng 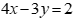 .
.
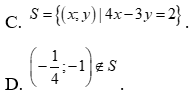
Lời giải
Lời giải
Chọn C
Ta có: 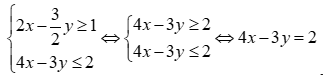 .
.
Vậy tập nghiệm của hệ bất phương trình là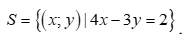 .
.
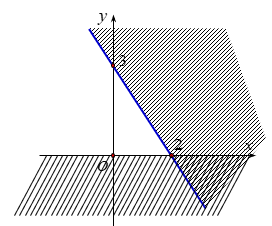
Câu 12:
Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ sau?
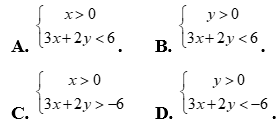
Lời giải
Chọn B
Dựa vào hình vẽ ta thấy đồ thị gồm hai đường thẳng 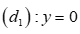 và đường thẳng
và đường thẳng 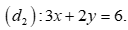
Miền nghiệm gồm phần phía trên trục hoành nên y nhận giá trị dương.
Lại có (0,0) thỏa mãn bất phương trình 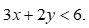
Câu 13:
Một người nông dân dự định trồng mía và ngô trên diện tích 8 sào đất (1 sào bằng 360m2). Nếu trồng mía thì trên mỗi sào cần 10công và thu lãi 1500000 đồng, nếu trồng ngô thì trên mỗi sào cần công và thu lãi 2000000 đồng. Biết tổng số công cần dùng không vượt quá 90công. Tính tổng số tiền lãi cao nhất mà người nông dân có thể thu được.
A. 14 (triệu đồng) B. 12 (triệu đồng)
C. 16 (triệu đồng) D. 13 (triệu đồng)
Lời giải
Chọn D
Gọi diện tích trồng mía là x,(đơn vị: sào, đk: 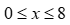 )
)
Gọi diện tích trồng ngô là y, (đơn vị: sào, đk: 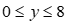 )
)
Diện tích trồng mía và ngô dự định là 8 sào nên ta có bpt: 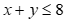
Tổng số công cần dùng cho cả hai loại không vượt quá 90 nên ta có bpt: 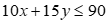
Tổng số tiền lãi thu được là: 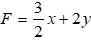 (đơn vị: triệu đồng)
(đơn vị: triệu đồng)
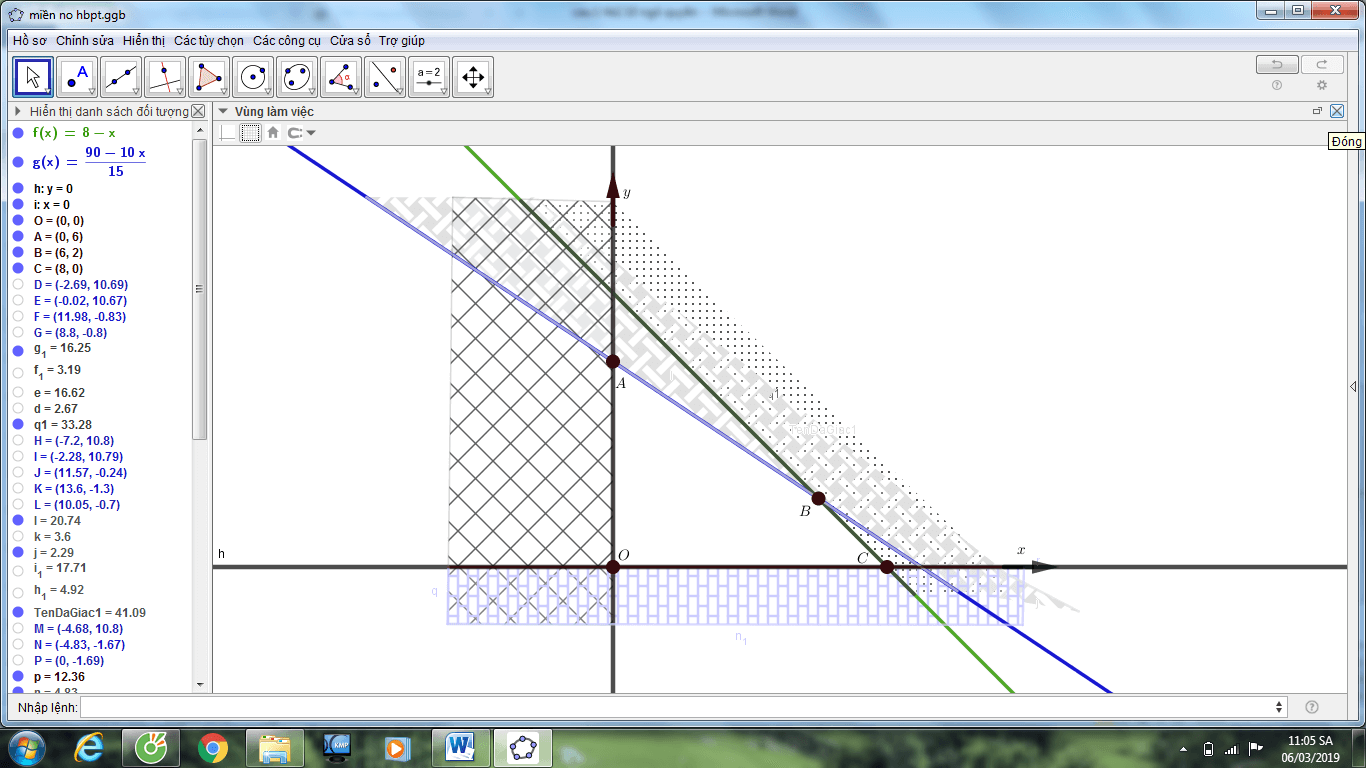
Khi đó, ta đưa về bài toán tìm (x,y) thỏa mãn hbpt: 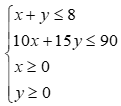 để
để 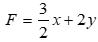 đạt giá trị lớn nhất.
đạt giá trị lớn nhất.
Biểu diễn hình học tập nghiệm hbpt ta được miền nghiệm cuả hbpt là tứ giác OABC kể cả biên,
với 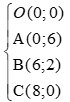
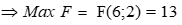
Câu 14 Tập nghiệm của bất phương trình 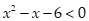 là:
là:
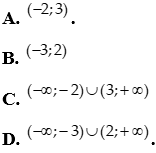
Lời giải
Chọn A
Ta có: 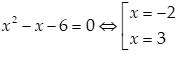 .
.
Bảng xét dấu:

Dựa vào bảng xét dấu ta có: 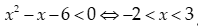 .
.
Câu 15:
Tam thức bậc hai 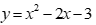 nhận giá trị dương khi và chỉ khi
nhận giá trị dương khi và chỉ khi
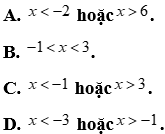
Lời giải
Chọn C
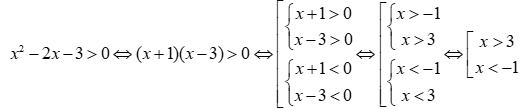 .
.
Vậy x<-1 hoặc x>3.
Câu 16:
Tập nghiệm của bất phương trình: 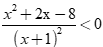 là:
là:
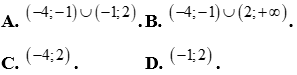
Lời giải
Chọn A
ĐKXĐ: 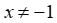 khi đó
khi đó 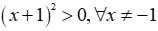 nên bất phương trình đã cho tương đương với BPT:
nên bất phương trình đã cho tương đương với BPT: 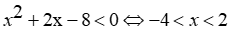 . Kết hợp đk ta được tập nghiệm:
. Kết hợp đk ta được tập nghiệm: 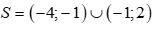
Câu 17:
Gọi M,m lần lượt là nghiệm nguyên lớn nhất và nhỏ nhất của bất phương trình 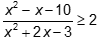 . Tính M+m.
. Tính M+m.
Lời giải
Chọn A
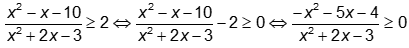
BXD:

Tập nghiệm của bất phương trình: 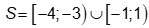
Nghiệm nguyên nhỏ nhất: m=-4 ; nghiệm nguyên lớn nhất: M=0
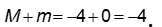
Câu 18:
Hệ bất phương trình 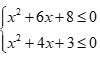 có tất cả bao nhiêu nghiệm nguyên?
có tất cả bao nhiêu nghiệm nguyên?
A. 5. B. 1.
C. 2. D. 0.
Lời giải
Chọn C
Ta có
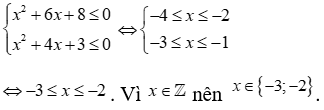
Vậy hệ bất phương trình có hai nghiệm nguyên thoả mãn.
Ghi nhớ: nắm kĩ qui tắc xét dấu nhị thức bậc nhất và tam thức bậc hai đồng thời nhớ cách tìm giao- hợp- hiệu của các tập hợp số.
Câu 19:
Cho hệ bất phương trình 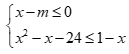 . Hệ đã cho có nghiệm khi và chỉ khi
. Hệ đã cho có nghiệm khi và chỉ khi
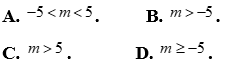
Lời giải
Chọn D
Hệ tương đương: 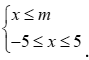 . Hệ có nghiệm
. Hệ có nghiệm 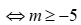 .
.
Câu 20:
Bất phương trình 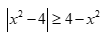 có tập nghiệm là:
có tập nghiệm là:
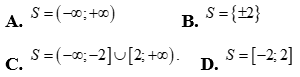
Lời giải
Chọn A
Ta có
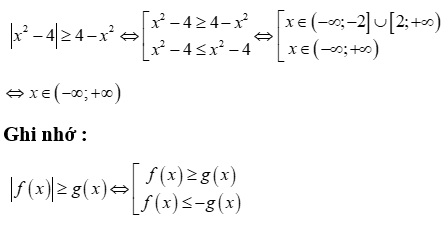
Câu 21:
Cho tam thức bậc hai 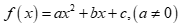 . Điều kiện cần và đủ để
. Điều kiện cần và đủ để 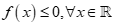 là:
là:
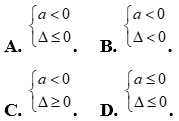
Lời giải
Chọn A
Câu 22:
Cho tam thức bậc hai 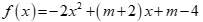 . Tìm m để f(x) luôn âm với mọi
. Tìm m để f(x) luôn âm với mọi ![]() .
.
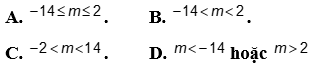
Lời giải
Chọn B
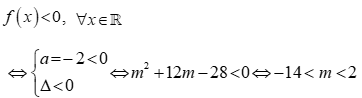
Câu 23:
Bất phương trình 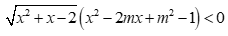 có nghiệm khi và chỉ khi
có nghiệm khi và chỉ khi 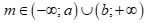 . Tính
. Tính ![]() .
.
A. 5. B. 1.
C. 2. D. 0.
Lời giải
Chọn B

Câu 24:
Tập nghiệm của bất phương trình 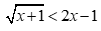 là :
là :
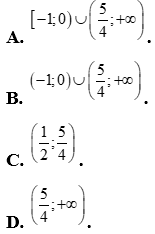
Lời giải
Chọn D
Ta có :
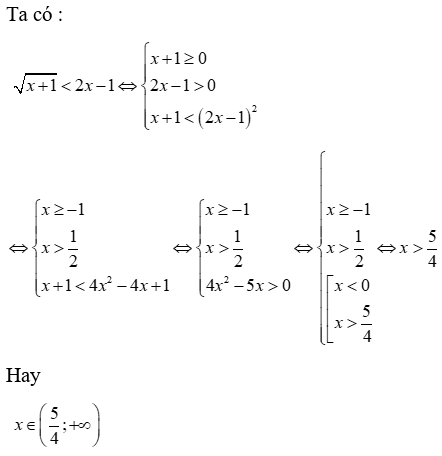
Ghi nhớ: Công thức được sử dụng:
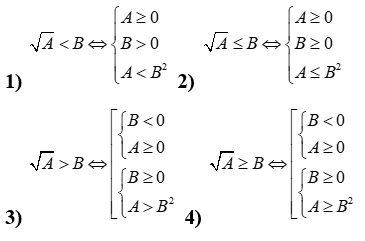
Câu 25:
Tam giác ABC có 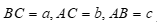 , góc
, góc 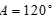 . Mệnh đề nào sau đây là đúng ?
. Mệnh đề nào sau đây là đúng ?
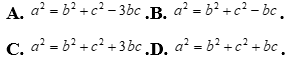
Lời giải
Chọn A
Áp dụng định lý cosin trong tam giác, ta có 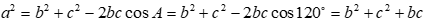 .
.
Câu 26:
Cho ![]() có
có 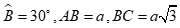 , trên cạnh BC lấy điểm M sao cho
, trên cạnh BC lấy điểm M sao cho 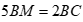 .
.
Tính độ dài đoạn .
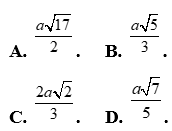
.
Lời giải
Chọn D
Chọn D
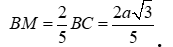 .
.
Áp dụng định lí cô sin cho tam giác ABM ta có:
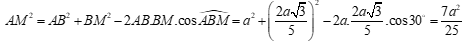 .
.
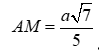 .
.
Câu 27:
Cho tam giác ABC có 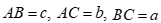 . Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Mệnh đề nào sau đây đúng?
. Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Mệnh đề nào sau đây đúng?
A. 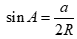 . B.
. B. 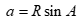 .
.
C. 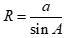 . D.
. D. 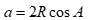 .
.
Lời giải
Chọn A
Theo định lí hàm số sin ta có
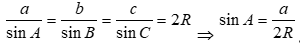 .
.
Câu 28:
Muốn đo khoảng cách từ người A trên bờ đến chiếc thuyền C neo đậu trên sông, người ta chọn một điểm B trên bờ và đo đượCab=160m, .Tính độ dài đoạn (xấp xỉ đến hàng phần trăm)
A. 74,87 (m) B. 74,88 (m)
C. 165,93 (m) D. 165,89 (m)
Lời giải
Chọn D
Ta có:
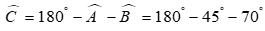
Áp dụng định lí hàm sin trong tam giác ABC ta có:
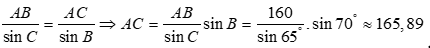 .
.
Ghi nhớ: Cho tam giác ABC có 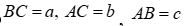 và R là bán kính đường tròn ngoại tiếp.
và R là bán kính đường tròn ngoại tiếp.
Ta có 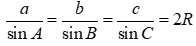 .
.
Câu 29:
Cho tam giác ABC có 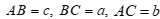 . Gọi M là trung điểm của BC. Mệnh đề nào sau đây đúng?
. Gọi M là trung điểm của BC. Mệnh đề nào sau đây đúng?
A. 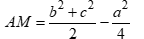 .
.
B. 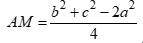 .
.
C. 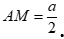 .
.
D. 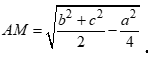 .
.
Lời giải
Theo công thức tính độ dài đường trung tuyến ta có:
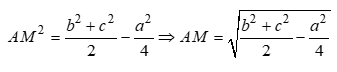
Câu 30:
Cho một tam giác có độ dài ba cạnh lần lượt là 13,14,15. Tính bán kính đường tròn nội tiếp tam giác đó.
A. 2. B. 4.
C. ![]() . D. 3.
. D. 3.
Lời giải
Chọn B
Ta có:
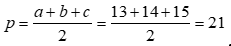 .
.
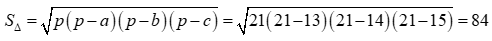 .
.
Lại có: 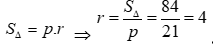 .
.
Vậy bán kính đường tròn nội tiếp tam giác r=4.
Vậy bán kính đường tròn nội tiếp tam giác .
Câu 31:
Cho tam giác ABC có BC=a, góc A bằng ![]() và hai đường trung tuyến BM,CN vuông góc với nhau. Diện tích tam giác ABC là
và hai đường trung tuyến BM,CN vuông góc với nhau. Diện tích tam giác ABC là
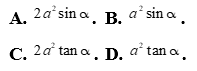
Lời giải
Chọn D
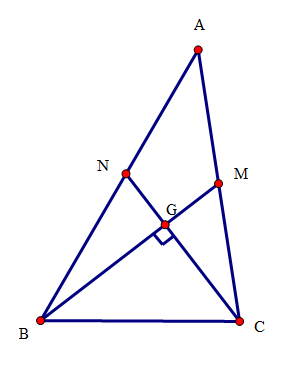
Ta có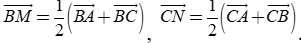 .
.
Do các đường trung tuyến BM,CN vuông góc với nhau nên
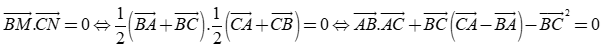
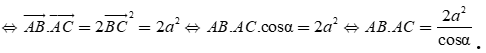 .
.
Diện tích tam giác ABC là 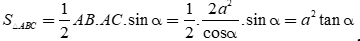 .
.
Câu 32:
Cho tam giác ABC có 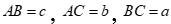 . Nhận dạng tam giác ABC biết
. Nhận dạng tam giác ABC biết 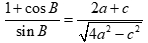 .
.
A. Tam giác cân. B. Tam giác vuông.
C. Tam giác đều. D. Tam giác có góc 60 độ.
Lời giải
Chọn A
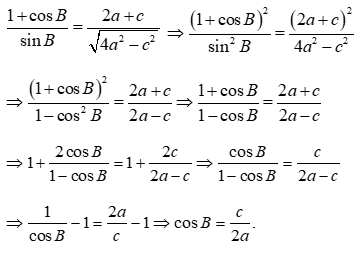
Mặt khác theo định lý cosin: 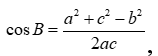 do vậy ta có:
do vậy ta có:
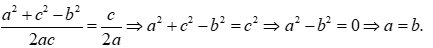
Vậy tam giác ABC cân tại C.
Vậy tam giác cân tại .
Câu 33: Tam giác ABC có 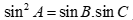 . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
A. 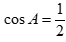 . B.
. B. 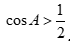 .
.
C. 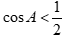 . D.
. D. 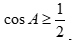 .
.
Lời giải
Chọn D
Áp dụng định lí sin: 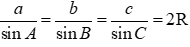 . Suy ra
. Suy ra 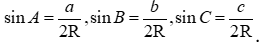 .
.
Thay vào biểu thức 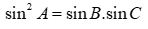 ta được:
ta được: 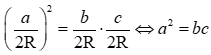 .
.
Do đó 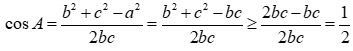 (vì
(vì 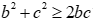 ).
).
Câu 34:
Trong các cặp bất phương trình dưới đây, cặp bất phương trình nào tương đương?
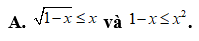
B. ![]() và
và ![]() .
.
C. 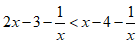 và
và 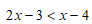 .
.
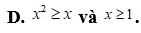
Lời giải
Chọn C
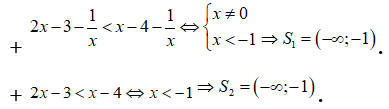
Nên cặp bất phương trình này tương đương.
Câu 35:
Bất phương trình 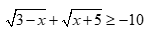 có bao nhiêu nghiệm?
có bao nhiêu nghiệm?
A. Hai nghiệm. B. Vô số nghiệm.
C. Vô nghiệm. D. Có một nghiệm
Lời giải
Chọn B
Điều kiện
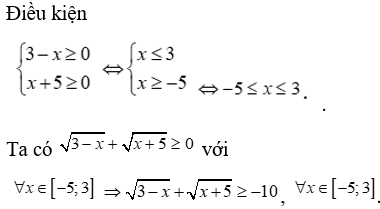
Vậy bất phương trình có vô số nghiệm.
II. Tự luận
Câu 36. Giải bất phương trình 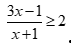 .
.
Lời giải
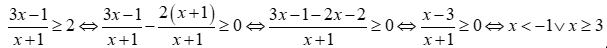
Câu 37. Tìm m để 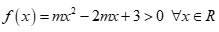 .
.
Lời giải
Với m=0 thì bất phương trình trở thành 3>0 luôn đúng với mọi ![]() nên m=0 thỏa mãn.
nên m=0 thỏa mãn.
Với ![]() thì bất phương trình nghiệm đúng với
thì bất phương trình nghiệm đúng với 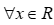 khi và chỉ khi
khi và chỉ khi 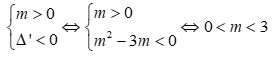 .
.
Kết luận: 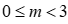 là điều kiện cần tìm.
là điều kiện cần tìm.
Câu 38. Cho tam giác ABC có 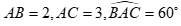 . Tính độ dài BC và .
. Tính độ dài BC và .
Lời giải
Áp dụng định lý cosin ta có 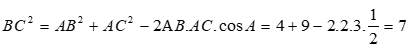
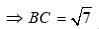 .
.
Áp dụng định lý sin ta có 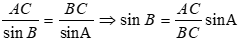
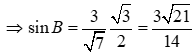 .
.
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Năm học 2023
Môn: Ngữ Văn 10
Thời gian làm bài: 90 phút
(Đề số 6)
I. Trắc nghiệm (2 điểm)
Câu 1:
Cho 2 đường thẳng 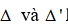 lần lượt có phương trình là
lần lượt có phương trình là 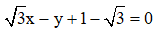 và
và 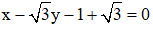 . Góc giữa 2 đường thẳng
. Góc giữa 2 đường thẳng 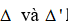 là:
là:
A. B.
C. D.
Câu 2: Điều kiện xác định của hàm số 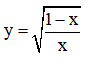 là
là

Câu 3: Tập nghiệm của bất phương trình 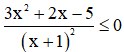 là
là
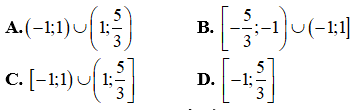
Câu 4: Giá trị của m để bất phương trình 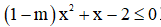 luôn đúng với mọi
luôn đúng với mọi 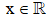 là
là
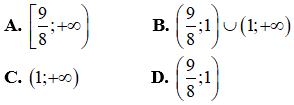
II. Tự luận (8 điểm)
Câu 5: (4 điểm)
Giải các bất phương trình sau:
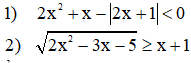
Câu 6: (1 điểm)
Tìm tất cả các giá trị của tham số a để bất phương trình 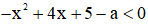 với
với 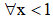
Câu7: (2 điểm)
Cho 2 điểm M(1;1), N(-2;3) và đường thẳng  có phương trình:
có phương trình: 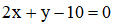
1) Xác định tọa độ điểm I thuộc đường thẳng  sao cho tam giác MNI vuông tại M.
sao cho tam giác MNI vuông tại M.
2) Xác định tọa độ điểm K thuộc đường thẳng  sao cho diện tích tam giác MNK bằng
sao cho diện tích tam giác MNK bằng 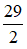 đvdt.
đvdt.
Câu 8: (1điểm) Cho 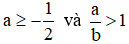 .Chứng minh rằng
.Chứng minh rằng 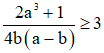 .
.
Đáp án và thang điểm
I. Phần trắc nghiệm khách quan: (2 điểm - Mỗi câu 0,5 điểm)
Câu 1: Chọn B
Ta có: 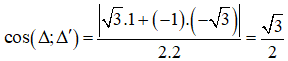
Vậy góc giữa hai đường thẳng 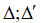 là .
là .
Câu 2: Chọn C
Hàm số 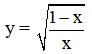 có nghĩa khi và chỉ khi
có nghĩa khi và chỉ khi
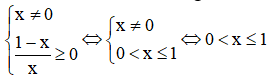
Câu 3: Chọn B
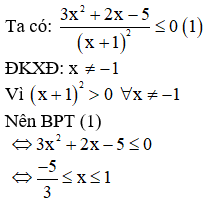
Kết hợp điều kiện, Vậy tập nghiệm của BPT đã cho là 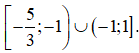 .
.
Câu 4: Chọn A
Bất phương trình 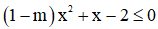 luôn đúng với mọi
luôn đúng với mọi 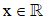
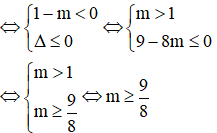
Vậy 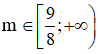 thì thỏa mãn yêu cầu bài toán.
thì thỏa mãn yêu cầu bài toán.
II. Phần tự luận
Câu 5.
1) Giải bất phương trình 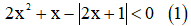
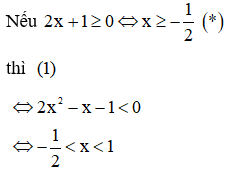
Kết hợp với điều kiện (*) ta có nghiệm của (1) là 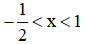 (0,75 điểm)
(0,75 điểm)
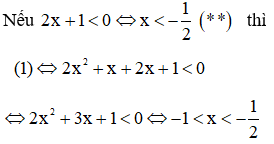
Kết hợp với điều kiện (**) thì (1) có nghiệm là 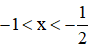 (0,75 điểm)
(0,75 điểm)
Vậy nghiệm của bất phương trình đã cho là 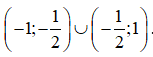 . (0,5 điểm)
. (0,5 điểm)
2) Giải bất phương trình 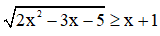
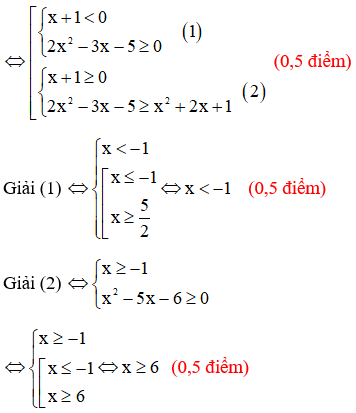
Vậy tập nghiệm của bất phương trình đã cho là 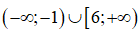 . (0,5 điểm)
. (0,5 điểm)
Câu 6.
Bất phương trình đã cho 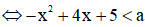 với mọi
với mọi 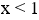
Gọi 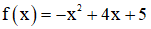 và g(x) = a thì f(x) có bảng biến thiên
và g(x) = a thì f(x) có bảng biến thiên
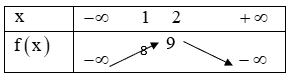
(0,5 điểm)
Dựa vào bảng biến thiên nhận thấy (*) nghiệm đúng khi 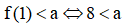 (0,25 điểm)
(0,25 điểm)
Vậy với a > 8 thì BPT đã cho có nghiệm. (0,25 điểm)
Câu 7.
1) 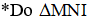 vuông tại M(1; 1) nên điểm I thuộc đường thẳng đi qua M và nhận
vuông tại M(1; 1) nên điểm I thuộc đường thẳng đi qua M và nhận 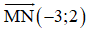 làm véc tơ pháp tuyến và có phương trình
làm véc tơ pháp tuyến và có phương trình 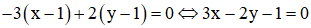 (0,5 điểm)
(0,5 điểm)
*Mặt khác: Do điểm 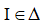 nên toạ độ của I là nghiệm của hệ phương trình
nên toạ độ của I là nghiệm của hệ phương trình
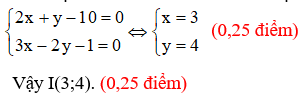
2) Do 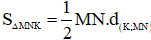 : Trong đó
: Trong đó 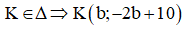
Đường thẳng MNcó véc tơ chỉ phương 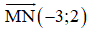 và đi qua
và đi qua 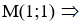 phương trình của đường thẳng MN là
phương trình của đường thẳng MN là 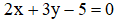 (0,25 điểm)
(0,25 điểm)
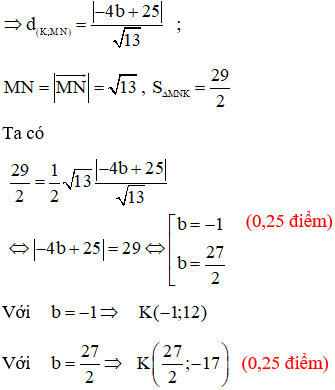
Vậy có 2 điểm K thỏa mãn bài ra là K(-1;12) và 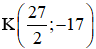 . (0,25 điểm)
. (0,25 điểm)
Câu 8.
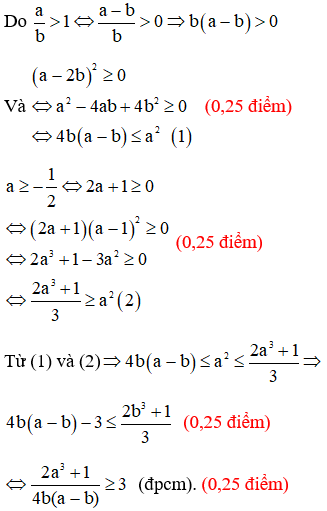

Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Năm học 2023
Môn: Ngữ Văn 10
Thời gian làm bài: 90 phút
(Đề số 7)
I. Trắc nghiệm (2 điểm)
Hãy chọn phương án trả lời đúng cho mỗi câu sau:
Câu 1: Cho 2 đường thẳng 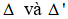 lần lượt có phương trình là x + 2y - 1 = 0
lần lượt có phương trình là x + 2y - 1 = 0
và 3x + y + 6 = 0. Góc giữa 2 đường thẳng 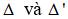 là:
là:

Câu 2: Điều kiện xác định của hàm số 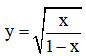 là
là

Câu 3: Tập nghiệm của bất phương trình 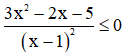 là
là
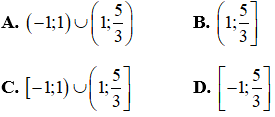
Câu 4: Giá trị của m để bất phương trình 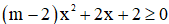 luôn đúng với mọi
luôn đúng với mọi 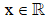 là
là
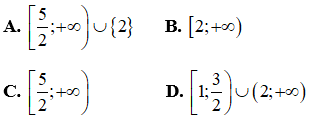
II. Tự luận (8 điểm)
Câu 5: (4 điểm)
Giải các bất phương trình sau:
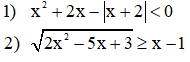
Câu 6: (1 điểm)
Tìm tất cả các giá trị của tham số m để bất phương trình 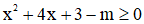 với
với 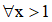 .
.
Câu 7: (2 điểm)
Cho 2 điểm A(-1;1), B(3;7) và đường thẳng d có phương trình: 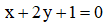
1) Xác định tọa độ điểm C thuộc đường thẳng d sao cho tam giác ABC vuông tại A.
2) Xác định tọa độ điểm D thuộc đường thẳng d sao cho diện tích tam giác ABD bằng 50.
Câu 8: (1điểm)
Cho 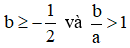 . Chứng minh rằng
. Chứng minh rằng 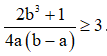 .
.
Đáp án và thang điểm
I. Phần trắc nghiệm khách quan: (2 điểm - Mỗi câu 0,5 điểm)
Câu 1: Chọn B
Ta có: 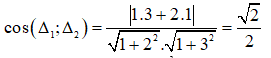
Suy ra góc giữa hai đường thẳng 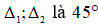 .
.
Câu 2: Chọn A
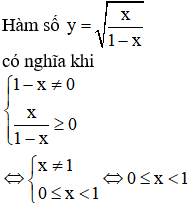
Câu 3: Chọn C
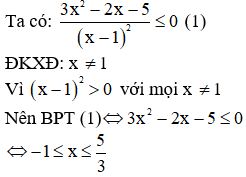
Kết hợp điều kiện, Vậy tập nghiệm của BPT đã cho là 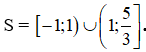 .
.
Câu 4: Chọn C
Bất phương trình 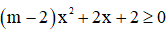 luôn đúng với mọi
luôn đúng với mọi 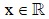 khi và chỉ khi
khi và chỉ khi
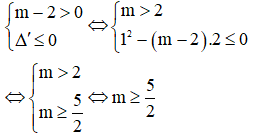
Vậy 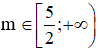 thì thỏa mãn yêu cầu bài toán.
thì thỏa mãn yêu cầu bài toán.
II. Phần tự luận
Câu 5.
1) Giải bất phươmg trình 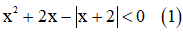
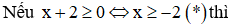
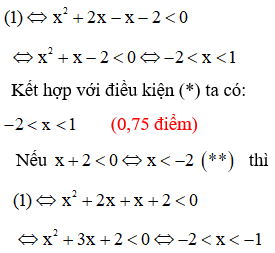
Kết hợp với điều kiện (**) thì (1) vô nghiệm (0,75 điểm)
Vậy nghiệm của bất phương trình đã cho là 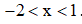 . (0,5 điểm)
. (0,5 điểm)
2) Giải bất phương trình 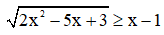
Ta có: 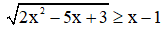
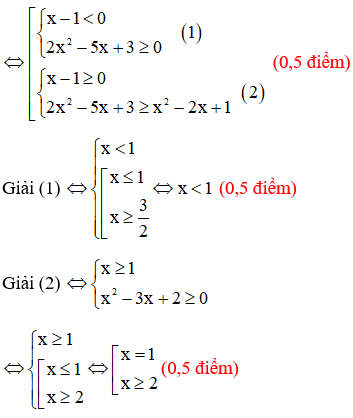
Vậy tập nghiệm của bất phương trình đã cho là 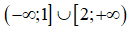 . (0,5 điểm)
. (0,5 điểm)
Câu 6.
Bất phương trình đã cho 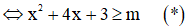 với mọi x >1
với mọi x >1
Gọi 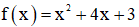 và g(x) = m thì g(x) có đồ thị là đường thẳng
và g(x) = m thì g(x) có đồ thị là đường thẳng
còn 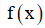 có bảng biến thiên
có bảng biến thiên
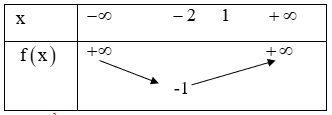
(0,5 điểm)
Dựa vào bảng biến thiên nhận thấy (*) đúng khi 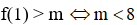 (0,25 điểm)
(0,25 điểm)
Vậy với 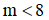 thì BPT đã cho có nghiệm. (0,25 điểm)
thì BPT đã cho có nghiệm. (0,25 điểm)
Câu 7.
1) Cho 2 điểm A(-1;1), B(3;7) và đường thẳng d có phương trình: 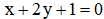 . Xác định tọa độ điểm C thuộc đường thẳng d sao cho tam giác ABC vuông tại A.
. Xác định tọa độ điểm C thuộc đường thẳng d sao cho tam giác ABC vuông tại A.
*Do 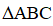 vuông tại A(-1; 1) nên điểm C thuộc đường thẳng đi qua A và nhận
vuông tại A(-1; 1) nên điểm C thuộc đường thẳng đi qua A và nhận 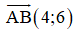 làm véc tơ pháp tuyến và có phương trình
làm véc tơ pháp tuyến và có phương trình 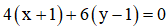
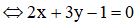 (0,5 điểm)
(0,5 điểm)
*Mặt khác: Do điểm nên toạ độ của C là nghiệm của hệ phương trình
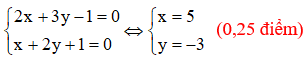
Vậy C(5;-3). (0,25 điểm)
2) Cho 2 điểm A(-1; 1), B(3; 7) và đường thẳng d có phương trình: 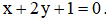 . Xác định tọa độ điểm D thuộc đường thẳng d sao cho diện tích tam giác ABD bằng 50.
. Xác định tọa độ điểm D thuộc đường thẳng d sao cho diện tích tam giác ABD bằng 50.
Do 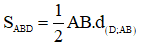
Trong đó 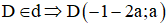
Đường thẳng AB có véc tơ chỉ phương 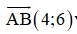 và đi qua A(-1;1)
và đi qua A(-1;1)
phương trình của đường thẳng AB là 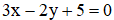 (0,25 điểm)
(0,25 điểm)
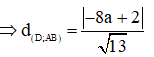 ;
;
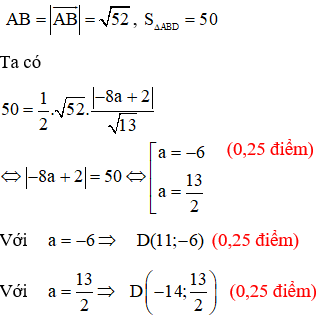
Câu 8. Cho 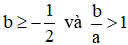 . Chứng minh rằng
. Chứng minh rằng 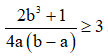 .
.
Giải: