Cho đường cong y = x^3. Viết phương trình tiếp tuyến của đường cong trong

Bài 1: Định nghĩa và ý nghĩa của đạo hàm

Bài 5 trang 156 Toán 11: Cho đường cong y = x³. Viết phương trình tiếp tuyến của đường cong trong các trường hợp:

a) Tại điểm (–1; –1);

b) Tại điểm có hoành độ bằng 2;

c) Biết hệ số góc của tiếp tuyến bằng 3.

Trả lời

Ta có:

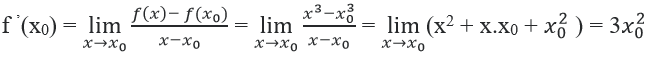
a) Với x₀ = –1 ⇒ f’(–1) = 3.

Vậy phương trình tiếp tuyến của đồ thị hàm số y = x³ tại điểm ( –1; –1) là :

y – y₀ = f’(x₀)(x – x₀) hay y + 1 = 3(x+1) ⇔ y = 3x + 2.

b) Với x₀ = 2 ⇒ f’(2) = 12 và y₀ = f(2) = 8.

Vậy phương trình tiếp tuyến của đồ thị hàm số y = x³ tại điểm có hoành độ bằng 2 là: y – y₀ = f’(x₀)(x – x₀) hay y – 8 = 12(x – 2) ⇔ y = 12x – 16.

c) Do hệ số góc của tiếp tuyến bằng 3 nên:

f’(x₀) = 3 ⇔ 3x₀² = 3 ⇔ x₀ = ±1.

+ Với x₀ = 1 ⇒ y₀ = 1. Phương trình tiếp tuyến cần tìm là:

y – 1 = 3(x – 1) hay y = 3x – 2.

+ Với x₀ = –1 ⇒ y₀ = –1. Phương trình tiếp tuyến cần tìm là:

y + 1 = 3(x + 1) hay y = 3x + 2.