Mỗi mặt phẳng chứa một cạnh bên và đường cao của hình chóp đều vuông góc với cạnh đối diện

Bài 4: Hai mặt phẳng vuông góc

Bài 3.28 trang 151 Sách bài tập Hình học 11: Cho hình chóp đều S.ABC. Chứng minh rằng:

a) Mỗi cạnh bên của hình chóp đó vuông góc với cạnh đối diện ;

b) Mỗi mặt phẳng chứa một cạnh bên và đường cao của hình chóp đều vuông góc với cạnh đối diện.

Lời giải:

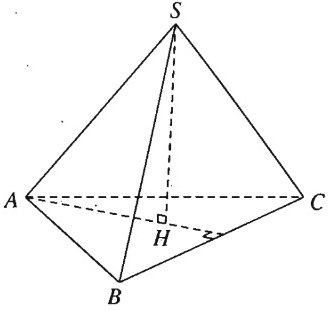
a) Vì S.ABC là hình chóp đều nên ∆ABC là tam giác đều và có SA = SB = SC. Do đó khi ta vẽ SH ⊥ (ABC) thì H là trọng tâm của tam giác đều ABC và ta có AH ⊥ BC. Theo định lí ba đường vuông góc ta có SA ⊥ BC.

Chứng minh tương tự ta có SB ⊥ AC và SC ⊥ AB

b) Vì BC ⊥ AH và BC ⊥ SH nên BC ⊥ (SAH)

Chứng minh tương tự ta có CA ⊥ (SBH) và AB ⊥ (SCH).