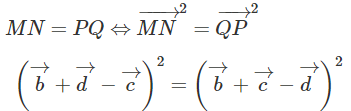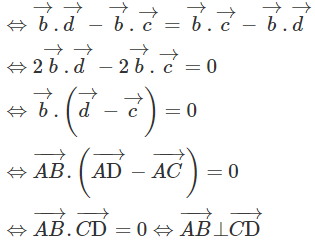Giải SBT Toán 11 Chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian
Giải SBT Toán 11 Chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian
Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán lớp 11 Chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian chi tiết giúp bạn biết cách làm bài tập về nhà môn Toán 11.

- Bài 1: Vectơ trong không gian
- Bài 2 : Hai đường thẳng vuông góc
- Bài 3 : Đường thẳng vuông góc với mặt phẳng
- Bài 4: Hai mặt phẳng vuông góc
- Bài 5: Khoảng cách
- Câu hỏi ôn tập chương 3
- Đề toán tổng hợp chương 3
- Câu hỏi trắc nghiệm chương 3
- Đề toán tổng hợp ôn tập cuối năm
Giải SBT Toán 11 Bài 1: Vectơ trong không gian
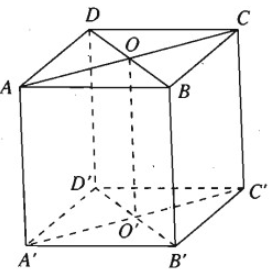
Bài 3.1 trang 129 Sách bài tập Hình học 11: Cho hình lập phương ABCDA’B’C’D’ cạnh a. Gọi O và O’ theo thứ tự là tâm của hai hình vuông ABCD và A’B’C’D’.
a) Hãy biểu diễn các vectơ AO→, AO'→, theo các vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho.
b) Chứng minh rằng
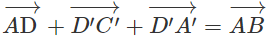
Lời giải:
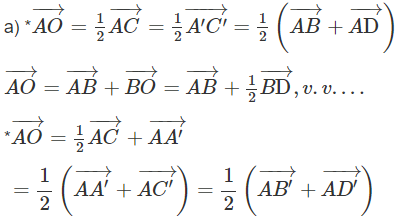
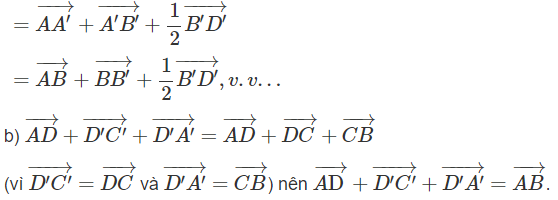
Bài 3.2 trang 129 Sách bài tập Hình học 11: Trong không gian cho điểm O và bốn điểm A, B, C, D phân biệt và không thẳng hàng. Chứng minh rằng điều kiện cần và đủ để bốn điểm A, B, C, D tạo thành một hình bình hành là:
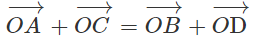
Lời giải:
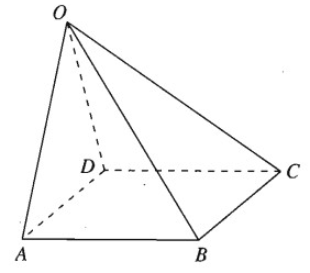
Giả sử bốn điểm A, B, C, D tạo thành một hình bình hành ta có:
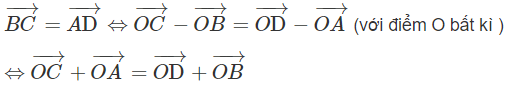
Ngược lại, giả sử ta có hệ thức:
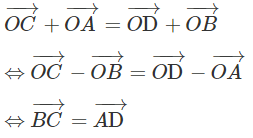
Vì A, B, C, D không thẳng hàng nên tứ giác ABCD là hình bình hành.
Bài 3.3 trang 129 Sách bài tập Hình học 11: Cho tứ diện ABCD. Gọi P và Q lần lượt là trung điểm của các cạnh AB và CD. Trên các cạnh AC và BD lần lượt ta lấy các điểm M, N sao cho
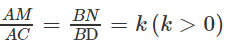
Chứng minh rằng ba vectơ PQ→, PM→, PN→ đồng phẳng.
Lời giải:
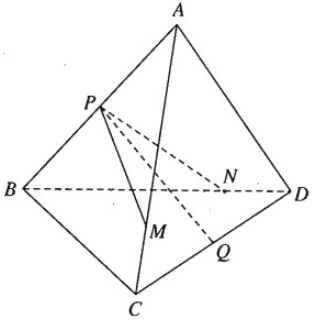
Ta có:
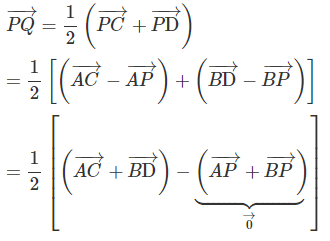
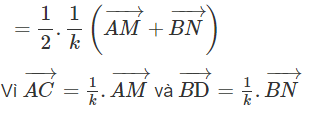
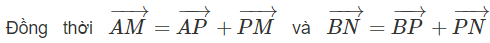
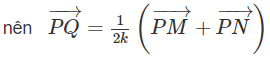
vì
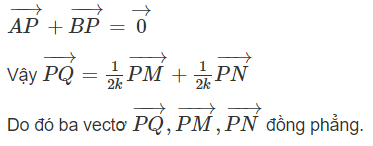
Giải SBT Toán 11 Bài 2: Hai đường thẳng vuông góc
Bài 3.8 trang 138 Sách bài tập Hình học 11: Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng:
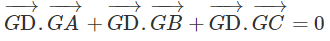
Lời giải:
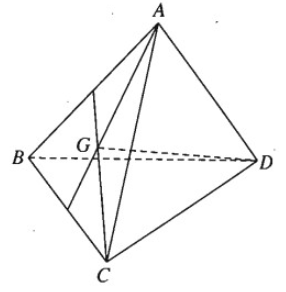
Ta có:
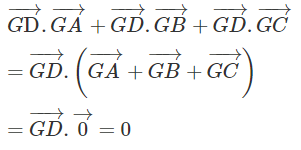
(Vì G là trọng tâm của tam giác ABCD nên
Bài 3.9 trang 138 Sách bài tập Hình học 11: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn AC, BD, AD và có MN = PQ . Chứng minh rằng AB ⊥ CD.
Lời giải:
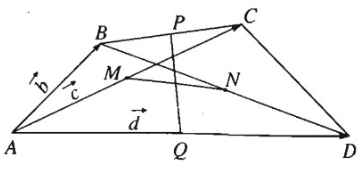
Ta cần chứng minh
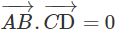
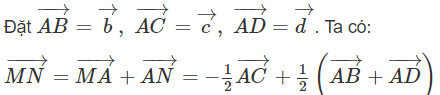
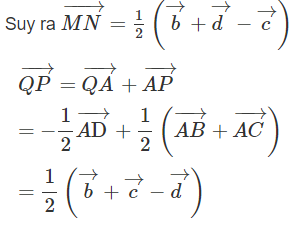
Theo giả thiết ta có: