Giải SBT Toán 11 Chương 3: Dãy số - Cấp số cộng và cấp số nhân

---

Giải SBT Toán 11 Chương 3: Dãy số - Cấp số cộng và cấp số nhân

Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán lớp 11 Chương 3: Dãy số - Cấp số cộng và cấp số nhân chi tiết giúp bạn biết cách làm bài tập về nhà môn Toán 11.

• Bài 1: Phương pháp quy nạp toán học
• Bài 2: Dãy số
• Bài 3: Cấp số cộng
• Bài 4: Cấp số nhân
• Ôn tập chương 3

Giải SBT Toán 11 Bài 2: Dãy số

Bài 3.9 trang 117 Sách bài tập Đại số 11: Viết năm số hạng đầu và khảo sát tính tăng, giảm của các dãy số (u_n) biết

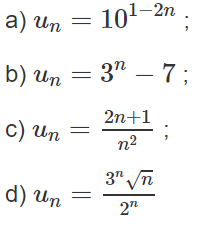
Lời giải:

a) Dự đoán dãy (un) giảm.

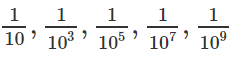
Để chứng minh, ta xét tỉ số . Vậy dãy số giảm

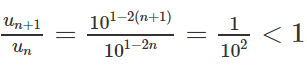
b) - 4, 2, 20, 74, 236. Xét dấu của hiệu u_{n + 1} - u_n

c) 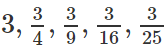. Làm tương tự câu b).

d)

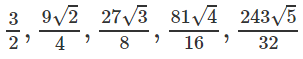
Phần tiếp theo có thể làm tương tự câu a).

Chú ý. Qua bốn bài tập trên, học sinh có thể rút ra nhận xét về tính hợp lí của việc xét hiệu u_{n + 1} - u_n hay tỉ số khi khảo sát tính đơn điệu của dãy số.

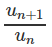
Bài 3.10 trang 117 Sách bài tập Đại số 11: Trong các dãy số (u_n) cho dưới đây, dãy số nào bị chặn dưới, bị chặn trên và bị chặn ?

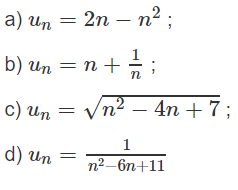
Lời giải:

a) Bị chặn trên vì u_n ≤ 1,∀n ∈ N^∗.

b) Bị chặn dưới vì u_n ≥ 2, ∀n ∈ N^∗.

c) Bị chặn dưới vì u_n ≥ √3, ∀n ∈ N^∗.

d) Bị chặn vì 0 < u_n ≤ 1/2, ∀n ∈ N^∗.

Bài 3.11 trang 118 Sách bài tập Đại số 11: Cho dãy số (u_n) xác định bởi

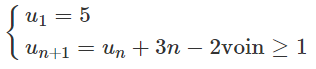
a) Tìm công thức tính (u_n) theo n ;

b) Chứng minh (u_n) là dãy số tăng.

Lời giải:

a) ĐS:

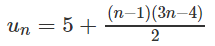
b) Tương tự bài Bài 2.1

Giải SBT Toán 11 Bài 3: Cấp số cộng

Bài 3.18 trang 123 Sách bài tập Đại số 11: Cho dãy số (u_n) với u_n = 1 - 7n

a) Khảo sát tính tăng, giảm của dãy số ;

b) Chứng minh dãy số trên là cấp số cộng. Lập công thức truy hồi của dãy số ;

c) Tính tổng 100 số hạng đầu của dãy số.

Lời giải:

a) Xét hiệu H = u_n+1 – u_n = 1 − 7(n + 1) − (1 − 7n) = −7 < 0, vậy dãy số giảm.

b) Do u_n+1 = u_n − 7 nên dãy số (u_n) là cấp số cộng với u¹ = −6; d = −7

Công thức truy hồi là

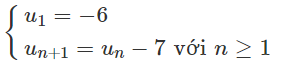
c) S₁₀₀ = -35250

Bài 3.19 trang 124 Sách bài tập Đại số 11: Trong các dãy số (u_n) sau đây, dãy số nào là cấp số cộng?

 a) u_n = 3n − 1;

 b) u_n = 2ⁿ + 1;

 c) u_n = (n+1)² − n²;

 d)

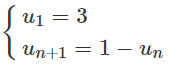
Lời giải:

 a) u_n+1 − u_n = 3(n + 1) − 1 − 3n + 1 = 3

 Vì u_n+1 = u_n + 3 nên (u_n) dãy số là cấp số cộng với u₁ = 2, d = 3.

 b) u_n+1 − u_n = 2ⁿ⁺¹ + 1 − 2ⁿ − 1 = 2ⁿ. Vì 2ⁿ không là hằng số nên dãy số (uⁿ) không phải là cấp số cộng.

 c) Ta có u_n = 2n + 1.

 Vì u_n+1 − u_n = 2(n + 1) + 1 − 2n − 1 = 2, nên dãy đã cho là cấp số cộng với u₁= 3; d = 2.

 d) Để chứng tỏ (un) không phải là cấp số cộng, ta chỉ cần chỉ ra, chẳng hạn u₃ − u₂ ≠ u₂ − u₁ là đủ.

Bài 3.20 trang 124 Sách bài tập Đại số 11: Tính số hạng đầu u₁ và công sai d của cấp số cộng (u_n) biết :

a)

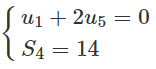
b)

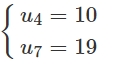
c)

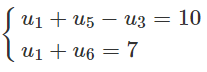
d)

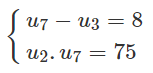
Lời giải:

a) u₁ = 8, d = −3.

b) u₁ = 1, d = 3.

c) u₁ = 36, d = −13.

d) u₁ = 3, d = 2 hoặc u₁ = −17, d = 2.