Giải SBT Toán 11 Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
Giải SBT Toán 11 Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán lớp 11 Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng chi tiết giúp bạn biết cách làm bài tập về nhà môn Toán 11.
- Bài 1: Phép biến hình - Bài 2: Phép tịnh tiến
- Bài 3: Phép đối xứng trục
- Bài 4: Phép đối xứng tâm
- Bài 5: Phép quay
- Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
- Bài 7: Phép vị tự
- Bài 8: Phép đồng dạng
- Câu hỏi ôn tập chương 1
- Đề toán tổng hợp chương 1
- Câu hỏi trắc nghiệm chương 1
Giải SBT Toán 11 Bài 1: Phép biến hình - Bài 2: Phép tịnh tiến
Bài 1.1 trang 10 Sách bài tập Hình học 11: Trong mặt phẳng tọa độ Oxy cho vectơ v = (2; −1) , điểm M = (3; 2). Tìm tọa độ của các điểm A sao cho:
a) A = Tv→(M)
b) M = Tv→(A)
Lời giải:
a) Giả sử A = (x; y). Khi đó
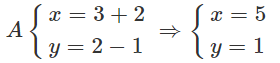
Vậy A = (5; 1)
b) Giả sử A = (x; y). Khi đó
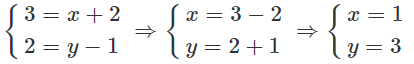
Vậy A = (1; 3)
Bài 1.2 trang 10 Sách bài tập Hình học 11: Trong mặt phẳng v→ = (−2;1) cho, đường thẳng d có phương trình 2x − 3y + 3 = 0, đường thẳng d1 có phương trình 2x − 3y − 5 = 0.
a) Viết phương trình của đường thẳng d’ là ảnh của d qua Tv→.
b) Tìm tọa độ của w→ có giá vuông góc với đường thẳng d để d1 là ảnh của d qua Tw→.
Lời giải:
a) Lấy một điểm thuộc d, chẳng hạn M = (0; 1).
Khi đó M′ = Tv→(M) = (0 − 2; 1 + 1) = (−2; 2) thuộc d'. Vì d' song song với d nên phương trình của nó có dạng 2x − 3y + C = 0. Do M' ∈ d′ nên 2.(−2) − 3.2 + C = 0. Từ đó suy ra C = 10 . Do đó d' có phương trình 2x − 3y + 10 = 0.
b) Lấy một điểm thuộc d, chẳng hạn M = (0; 1). Đường thẳng d2 qua M vuông góc với có vectơ chỉ phương là v→ = (2; −3). Do đó phương trình của d2 là
. Gọi M' là giao của d1 với d2 thì tọa độ của nó phải thỏa mãn hệ phương trình:
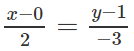
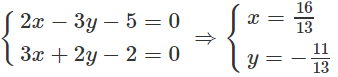
Từ đó suy ra
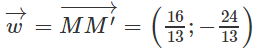
Giải SBT Toán 11 Bài 3: Phép đối xứng trục
Bài 1.6 trang 16 Sách bài tập Hình học 11: Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 = 0 và đường tròn (C) có phương trình x2 + y2 − 2x + 4y – 4 = 0. Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox
Lời giải:
Gọi M′, d′ và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox . Khi đó M′ = (3;5) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục:
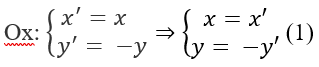
Thay (1) vào phương trình của đường thẳng d ta được 3x′ − 2y′ − 6 = 0. Từ đó suy ra phương trình của d' là 3x − 2y – 6 = 0
Thay (1) vào phương trình của (C) ta được x′2 + y′2 − 2x′ + 4y′ − 4 = 0 . Từ đó suy ra phương trình của (C') là (x − 1)2 + (y − 2)2 = 9.
Cũng có thể nhận xét (C) có tâm là I(1; −2), bán kính bằng 3, từ đó suy ra tâm I' của (C') có tọa độ (1;2) và phương trình của (C') là (x − 1)2 + (y − 2)2 = 9
Bài 1.7 trang 16 Sách bài tập Hình học 11: Trong mặt phẳng Oxy cho đường thẳng d có phương trình x − 5y + 7 = 0 và đường thẳng d’ có phương trình 5x – y – 13 = 0. Tìm phép đối xứng trục biến d thành d’.
Lời giải:
Dễ thấy d và d' không song song với nhau. Do đó trục đối xứng Δ của phép đối xứng biến d thành d' chính là đường phân giác của góc tạo bởi d và d'. Từ đó suy ra Δ có phương trình:
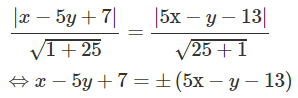
Từ đó tìm được hai phép đối xứng qua các trục:
Δ1 có phương trình: x + y – 5 = 0,
Δ2 có phương trình: x – y – 1 = 0.
Bài 1.8 trang 16 Sách bài tập Hình học 11: Tìm các trục đối xứng của hình vuông
Lời giải:
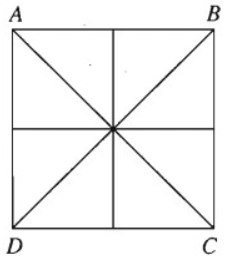
Cho hình vuông ABCD. Gọi F là phép đối xứng trục d biến hình vuông đó thành chính nó. Lí luận tương tự, ta thấy A chỉ có thể biến thành các điểm A, B, C hoặc D
- Nếu A biến thành chính nó thì C chỉ có thể biến thành chính nó và B biến thành D. Từ đó suy ra F là phép đối xứng qua trục AC
- Nếu A biến thành B thì d là đường trung trực của AB. Khi đó C biến thành D.
Các trường hợp khác lập luận tương tự. Do đó hình vuông ABCD có bốn trục đối xứng là các đường thẳng AC, BD và các đường trung trực của AB và BC.
