Giải SBT Toán 11 Chương 4: Giới hạn

---

Giải SBT Toán 11 Chương 4: Giới hạn

Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán lớp 11 Chương 4: Giới hạn chi tiết giúp bạn biết cách làm bài tập về nhà môn Toán 11.

• Bài 1: Giới hạn của dãy số
• Bài 2: Giới hạn của hàm số
• Bài 3: Hàm số liên tục
• Ôn tập chương 4

Giải SBT Toán 11 Bài 1: Giới hạn của dãy số

Bài 4.1 trang 156 Sách bài tập Đại số 11: Biết rằng dãy số (u_n) có giới hạn là 0. Giải thích vì sao dãy số (v_n) với v_n = |u_n| cũng có giới hạn là 0. Chiều ngược lại có đúng không?

Lời giải:

Vì (u_n) có giới hạn là 0 nên |u_n| có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.

Mặt khác, |v_n| = ||u_n|| = |u_n|. Do đó, |v_n| cũng có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi. Vậy (v_n) có giới hạn là 0.

(Chứng minh tương tự, ta có chiều ngược lại cũng đúng).

Bài 4.2 trang 156 Sách bài tập Đại số 11: Cho biết dãy số (u_n) có giới hạn hữu hạn, còn dãy số (v_n) không có giới hạn hữu hạn. Dãy số (u_{n + vn) có thể có giới hạn hữu hạn không?}

Lời giải:

Dãy (u_n + v_n) không có giới hạn hữu hạn.

Thật vậy, giả sử ngược lại (u_n + v_n) có giới hạn hữu hạn.

Khi đó, các dãy số (u_n + v_n) và (u_n) cùng có giới hạn hữu hạn, nên hiệu của chúng cũng là một dãy có giới hạn hữu hạn, nghĩa là dãy số có số hạng tổng quát là u_n + v_n − u_n = v_n có giới hạn hữu hạn. Điều này trái với giả thiết (v_n) không có giới hạn hữu hạn.

Bài 4.3 trang 156 Sách bài tập Đại số 11: a) Cho hai dãy số (u_n) và (vn). Biết lim u_n = −∞ và v_n ≤ u_n với mọi n. Có kết luận gì về giới hạn của dãy (v_n) khi n → +∞?

b) Tìm v_n với v_n = -n!

Lời giải:

a) Vì lim u_n = −∞ nên lim(−u_n) = +∞. Do đó (−u_n) có thể lớn hơn một số dương lớn tuỳ ý, kể từ một số hạng nào đó trở đi. (1)

Mặt khác, vì v_n ≤ u_n với mọi n nên (−v_n) ≥ (−u_n) với mọi n. (2)

Từ (1) và (2) suy ra (−v_n) có thể lớn hơn một số dương lớn tuỳ ý, kể từ một số hạng nào đó trở đi. Do đó, lim(−v_n) = +∞ hay lim v_n = −∞

b) Xét dãy số (u_n) = −n

Ta có - n! < - n hay v_n < u_n với mọi n. Mặt khác, lim u_n = lim(−n) = −∞

Từ kết quả câu a) suy ra lim v_n = lim(−n!) = −∞

Giải SBT Toán 11 Bài 2: Giới hạn của hàm số

Bài 4.18 trang 165 Sách bài tập Đại số 11: Dùng định nghĩa tìm các giới hạn

a)

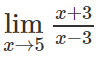
b)

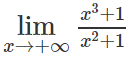
Lời giải:

a) = -4

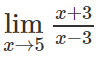
b) = +∞

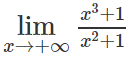
Bài 4.19 trang 165 Sách bài tập Đại số 11: Cho hàm số

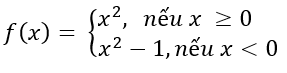
a) Vẽ đồ thị của hàm số f(x). Từ đó dự đoán về giới hạn của f(x) khi x → 0

b) Dùng định nghĩa chứng minh định nghĩa trên

Lời giải:

Bài 4.20 trang 165 Sách bài tập Đại số 11: a) Chứng minh rằng hàm số y = sinx không có giới hạn khi x → +∞

b) Giải thích bằng đồ thị kết luận ở câu a).

Lời giải:

a) Xét hai dãy số (a_n) với a_n = 2nπ và (b_n) với (b_n) = π/2 + 2nπ (n ∈ N^∗)

Ta có, lim a_n = lim 2nπ = +∞;

Lim b_n = lim(π/2 + 2nπ) = lim n(π/2n + 2π) = +∞

lim sin a_n = lim sin2nπ = lim 0 = 0

lim sin b_n = lim sin(π/2 + 2nπ) = lim 1 = 1

Như vậy, a_n → +∞, b_n →+∞ nhưng lim sin a_n ≠ lim sin b_n. Do đó, theo định nghĩa, hàm số y = sinx không có giới hạn khi x → +∞