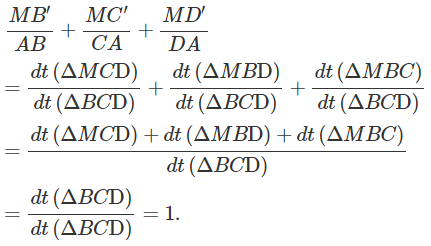Cho tứ diện ABCD và điểm M nằm trong tam giác BCD

Câu hỏi ôn tập chương 2

Bài 2.38 trang 81 Sách bài tập Hình học 11: Cho tứ diện ABCD và điểm M nằm trong tam giác BCD.

a) Dựng đường thẳng qua M song song với hai mặt phẳng (ABC) và (ABD). Giả sử đường thẳng này cắt mặt phẳng (ACD) tại B'.

Chứng minh rằng AB', BM và CD đồng quy tại một điểm.

b) Chứng minh

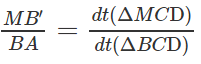
c) Đường thẳng song song với hai mặt phẳng (ACB) và (ACD) kẻ từ M cắt (ABD) tại C' và đường thẳng song song với hai mặt phẳng (ADC) và (ADB) kẻ từ M cắt (ABC) tại D'. Chứng minh rằng

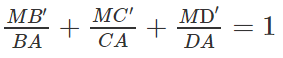
Lời giải:

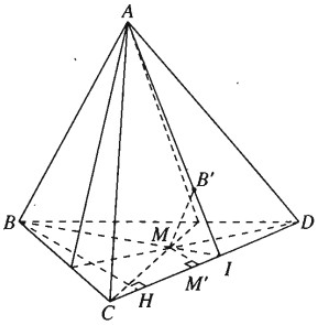
a) MB' qua M và song song với (ABC) và (ABD) ⇒ MB′ song song với giao tuyến AB của hai mặt phẳng này. Ta có: MB′ // AB nên MB' và AB xác định một mặt phẳng. Giả sử MB cắt AB' tại I.

Ta có: I ∈ BM ⇒ I ∈ (BCD)

I ∈ AB′ ⇒ I ∈ (ACD)

Nên I ∈ (BCD) ∩ (ACD) = CD

Có: I ∈ CD

Vậy ba đường thẳng AB', BM và CD đồng quy tại I.

b) MB′ // AB

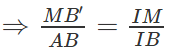
Kẻ MM′ ⊥ CD và BH ⊥ CD

Ta có: MM′ // BH

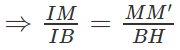
Mặt khác:

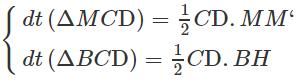
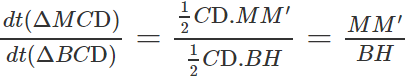
Do đó:

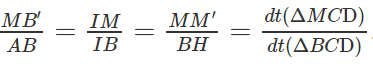
Vậy

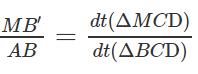
c) Tương tự ta có:

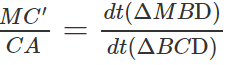
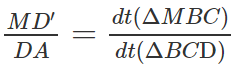
Vậy: