Chứng minh rằng f′(x) = 0 ∀x ∈ R

Bài 3: Đạo hàm của hàm số lượng giác

Bài 5.51 trang 208 Sách bài tập Đại số 11: Chứng minh rằng f′(x) = 0 ∀x ∈ R , nếu:

a) f(x) = 3(sin⁴x + cos⁴x) − 2(sin⁶x + cos⁶x);

b) f(x) = cos⁶x + 2sin⁴x.cos²x + 3sin²x.cos⁴x + sins⁴x

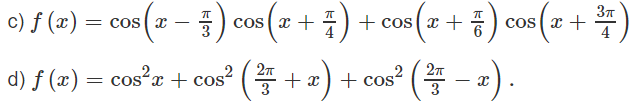
Lời giải:

Cách 1. Chứng minh các biểu thức đã cho không phụ thuộc vào x.

Từ đó suy ra f′(x) = 0.

a) f(x) = 1 ⇒ f′(x) = 0;

b) f(x) = 1 ⇒ f′(x) = 0;

c) f(x) = (√2 − √6)/4 ⇒ f′(x) = 0;

d) f(x) = 3/2 ⇒ f′(x) = 0.

Cách 2. Lấy đạo hàm của f(x) rồi chứng minh rằng f′(x) = 0.