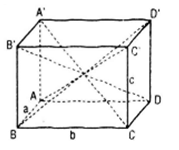
Cho hình hộp ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = c

Bài 4: Hai mặt phẳng vuông góc

Bài 22 (trang 111 sgk Hình học 11 nâng cao): Cho hình hộp ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = c. Nếu AC’ = BD' = B’D = 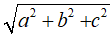thì hình hộp đó có phải là hình hộp chữ nhật không? Vì sao?

Lời giải:

Áp dụng tính chất tổng bình phương hai đường chéo hình bình hành bằng tổng bình phương 4 cạnh của nó (BT 38, 4, chương II)

Ta có :

AC'²+A'C²=2(AA'²+A'C²)

B'D²+BD'²=2(BB'²+BD²)

AC'²+A'C²+BD'²+BD'²

= 2(c²+c²+AC²+BD²)

= 4(a²+b²+c²)

A’C = AC’ = B’D = BD’.

AA’C’C và BB’D’D là các hình chữ nhật.

Từ đó suy ra AA’ ⊥ AC và AA’ ⊥ BD . Do đó AA’ ⊥ (ABCD), tức hình hộp ABCD. A’B’C’D’ là hình hộp chữ nhật.