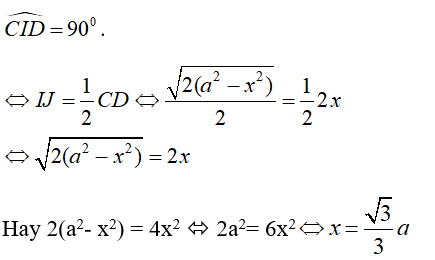Cho hai tam giác ACD, BCD nằm trên hai mặt phẳng

Bài 4: Hai mặt phẳng vuông góc

Bài 27 (trang 112 sgk Hình học 11 nâng cao): Cho hai tam giác ACD, BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a, CD = 2x. Gọi I, J lần lượt là trung điểm của AB và CD

a) Tính AB, IJ theo a và x.

b) Với giá trị nào của x thì hai mp(ABC) và (ABD) vuông góc?

Lời giải:

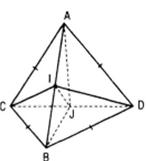
a)

+) Tam giác ACD có AC = AD = a

nên tam giác ACD cân tại A.

Có AJ là đường trung tuyến nên đồng thời là đường cao:

AJ ⊥ CD

b)

+Tam giác ABC có AC = BC

nên tam giác ABC cân tại C,

có CI là đường trung tuyến nên đồng thời là đường cao:

CI ⊥ AB (3)

Tam giác ABD cân tại D có DI là đường trung tuyến nên

DI ⊥ AB (4)

Hai mp (ABC) và (ABD) cắt nhau theo giao tuyến là AB (5)

Từ (3) , (4) và (5) suy ra góc giữa hai mp(ABC) và (ABD) là góc CID.

Vậy để hai mặt phẳng này vuông góc với nhau khi và chỉ khi